תרגום מטריצה ​​הפוך. הגדרת מטריצה ​​הפוכה קיום וייחודיות

שתהיה מטריצה ​​מרובעת מסדר n'י

מטריצה ​​A -1 נקראת מטריצה ​​הפוכהביחס למטריצה ​​A, אם A*A -1 = E, כאשר E היא מטריצת הזהות של הסדר ה-n.

מטריצת זהות- מטריצה ​​מרובעת כזו שבה כל האלמנטים לאורך האלכסון הראשי, העוברים מהפינה השמאלית העליונה לפינה הימנית התחתונה, הם אחדים, והשאר הם אפסים, למשל:

מטריצה ​​הפוכהעשוי להתקיים רק למטריצות מרובעותהָהֵן. עבור אותן מטריצות שבהן מספר השורות והעמודות חופפים.

משפט לתנאי קיום של מטריצה ​​הפוכה

כדי שלמטריקס תהיה מטריצה ​​הפוכה, יש צורך ומספיק שהיא תהיה לא יחידה.

המטריצה ​​A = (A1, A2,...A n) נקראת לא מנוון, אם וקטורי העמודה הם בלתי תלויים באופן ליניארי. מספר וקטורי העמודות הבלתי תלויים באופן ליניארי של מטריצה ​​נקרא דרגת המטריצה. לכן, ניתן לומר שכדי שתתקיים מטריצה ​​הפוכה, יש צורך ומספיק שדרגת המטריצה ​​תהיה שווה למימד שלה, כלומר. r = n.

אלגוריתם למציאת המטריצה ​​ההפוכה

1. כתוב מטריצה ​​A לטבלה לפתרון מערכות משוואות בשיטת גאוס והקצה לה מטריצה ​​E מימין (במקום הצדדים הימניים של המשוואות).
2. באמצעות טרנספורמציות ג'ורדן, צמצם מטריצה ​​A למטריצה ​​המורכבת מעמודות יחידות; במקרה זה, יש צורך להפוך את המטריצה ​​E בו זמנית.
3. במידת הצורך, סדר מחדש את השורות (המשוואות) של הטבלה האחרונה כך שמתחת למטריצה ​​A של הטבלה המקורית תקבל את מטריצת הזהות E.
4. רשום את המטריצה ​​ההפוכה A -1, שנמצאת בטבלה האחרונה מתחת למטריצה ​​E של הטבלה המקורית.

דוגמה 1

עבור מטריצה ​​A, מצא את המטריצה ​​ההפוכה A -1

פתרון: אנו כותבים מטריצה ​​A ומקצה את מטריצת הזהות E לימין באמצעות טרנספורמציות ירדן, אנו מצמצמים מטריצה ​​A למטריצת הזהות E. החישובים ניתנים בטבלה 31.1.

הבה נבדוק את נכונות החישובים על ידי הכפלת המטריצה ​​המקורית A והמטריצה ​​ההפוכה A -1.

כתוצאה מכפל מטריצה ​​התקבלה מטריצת הזהות. לכן, החישובים בוצעו כהלכה.

תשובה:

פתרון משוואות מטריצות

משוואות מטריקס יכולות להיראות כך:

AX = B, HA = B, AXB = C,

כאשר A, B, C הם המטריצות שצוינו, X היא המטריצה ​​הרצויה.

משוואות מטריצה ​​נפתרות על ידי הכפלת המשוואה במטריצות הפוכות.

לדוגמה, כדי למצוא את המטריצה ​​מהמשוואה, עליך להכפיל את המשוואה הזו בצד שמאל.

לכן, כדי למצוא פתרון למשוואה, צריך למצוא את המטריצה ​​ההפוכה ולהכפיל אותה במטריצה ​​בצד ימין של המשוואה.

משוואות אחרות נפתרות באופן דומה.

דוגמה 2

פתרו את המשוואה AX = B if

פִּתָרוֹן: מאחר והמטריצה ​​ההפוכה שווה ל (ראה דוגמה 1)

שיטת מטריקס בניתוח כלכלי

יחד עם אחרים, הם משמשים גם שיטות מטריצות. שיטות אלו מבוססות על אלגברה ליניארית ומטריצה ​​וקטורית. שיטות כאלה משמשות למטרות ניתוח של תופעות כלכליות מורכבות ורב-ממדיות. לרוב, שיטות אלו משמשות כאשר יש צורך לבצע הערכה השוואתית של תפקוד הארגונים והחלוקות המבניות שלהם.

בתהליך יישום שיטות ניתוח מטריצות ניתן להבחין במספר שלבים.

בשלב הראשוןנוצרת מערכת של אינדיקטורים כלכליים ועל בסיסה מורכבת מטריצה ​​של נתונים ראשוניים, שהיא טבלה שבה מספרי מערכת מוצגים בשורות הפרטניות שלה (i = 1,2,....,n), ובעמודות אנכיות - מספרי אינדיקטורים (j = 1,2,....,m).

בשלב השניעבור כל עמודה אנכית, מזוהה הגדול מבין ערכי האינדיקטור הזמינים, שנלקח כאחד.

לאחר מכן, כל הסכומים המשתקפים בעמודה זו מחולקים בערך הגדול ביותר ונוצרת מטריצה ​​של מקדמים מתוקננים.

בשלב השלישיכל מרכיבי המטריצה ​​בריבוע. אם יש להם משמעות שונה, אז לכל מחוון מטריצה ​​מוקצה מקדם משקל מסוים ק. ערכו של האחרון נקבע על ידי חוות דעת מומחה.

על האחרון, שלב רביעינמצאו ערכי דירוג Rjמקובצים לפי סדר העלייה או הירידה שלהם.

יש להשתמש בשיטות המטריצה ​​המפורטות, למשל, בניתוח השוואתי של פרויקטי השקעה שונים, וכן בהערכת אינדיקטורים כלכליים אחרים של פעילות ארגונים.

על מנת למצוא את המטריצה ​​ההפוכה באינטרנט, תצטרך לציין את גודל המטריצה ​​עצמה. כדי לעשות זאת, לחץ על הסמלים "+" או "-" עד שתהיה מרוצה ממספר העמודות והשורות. לאחר מכן, הזן את האלמנטים הנדרשים בשדות. להלן כפתור "חשב" - בלחיצה עליו תקבלו תשובה על המסך עם פתרון מפורט.

באלגברה לינארית, לעיתים קרובות יש להתמודד עם תהליך חישוב המטריצה ​​ההפוכה. הוא קיים רק עבור מטריצות לא מובעות ומטריצות מרובעות בתנאי שהדטרמיננטה אינה אפס. באופן עקרוני, חישוב זה לא קשה במיוחד, במיוחד אם אתה מתמודד עם מטריצה ​​קטנה. אבל אם אתה צריך חישובים מורכבים יותר או בדיקה כפולה יסודית של ההחלטה שלך, עדיף להשתמש במחשבון מקוון זה. בעזרתו תוכלו לפתור במהירות ובדייקנות מטריצה ​​הפוכה.

באמצעות מחשבון מקוון זה, אתה יכול להקל בהרבה על החישובים שלך. בנוסף, זה עוזר לגבש את החומר המתקבל בתיאוריה - הוא מעין סימולטור למוח. זה לא צריך להיחשב כתחליף לחישובים ידניים זה יכול לתת לך הרבה יותר, מה שמקל על הבנת האלגוריתם עצמו. חוץ מזה, זה אף פעם לא מזיק לבדוק את עצמך פעמיים.

הגדרה 1:מטריצה ​​נקראת יחיד אם הקובע שלה הוא אפס.

הגדרה 2:מטריצה ​​נקראת לא יחידה אם הקובע שלה אינו שווה לאפס.

המטריצה ​​"A" נקראת מטריצה ​​הפוכה, אם מתקיים התנאי A*A-1 = A-1 *A = E (מטריצת יחידה).

מטריצה ​​מרובעת ניתנת להפיכה רק אם היא לא יחידה.

סכימה לחישוב המטריצה ​​ההפוכה:

1) חשב את הקובע של מטריצה ​​"A" אם ∆ A = 0, אז המטריצה ​​ההפוכה לא קיימת.

2) מצא את כל ההשלמות האלגבריות של המטריצה ​​"A".

3) צור מטריצה ​​של תוספות אלגבריות (Aij)

4) טרנספוזיציה של המטריצה ​​של משלים אלגבריים (Aij )T

5) הכפל את המטריצה ​​המוטרפת בהיפוך של הקובע של מטריצה ​​זו.

6) בצע בדיקה:

במבט ראשון זה אולי נראה מסובך, אבל למעשה הכל מאוד פשוט. כל הפתרונות מבוססים על פעולות אריתמטיות פשוטות כאשר הפתרון הוא לא להתבלבל עם הסימנים "-" ו-"+" ולא לאבד אותם.

כעת נפתור יחד בעיה מעשית על ידי חישוב המטריצה ​​ההפוכה.

משימה: מצא את המטריצה ​​ההפוכה "A" המוצגת בתמונה למטה:

אנחנו פותרים הכל בדיוק כפי שמצוין בתוכנית לחישוב המטריצה ​​ההפוכה.

1. הדבר הראשון שצריך לעשות הוא למצוא את הקובע של המטריצה ​​"A":

הֶסבֵּר:

פישטנו את הקובע שלנו באמצעות הפונקציות הבסיסיות שלו. ראשית, הוספנו לשורה השנייה והשלישית את מרכיבי השורה הראשונה, כפול מספר אחד.

שנית, שינינו את העמודה ה-2 וה-3 של הקובע, ולפי תכונותיו שינינו את הסימן שלפניו.

שלישית, הוצאנו את הגורם המשותף (-1) של השורה השנייה, ובכך שינינו שוב את השלט, והוא הפך לחיובי. פישטנו גם את שורה 3 באותו אופן כמו בתחילת הדוגמה.

יש לנו דטרמיננט משולש שהיסודות שלו מתחת לאלכסון שווים לאפס, ולפי תכונה 7 הוא שווה למכפלת האלמנטים האלכסוניים. בסוף קיבלנו ∆ A = 26, לכן המטריצה ​​ההפוכה קיימת.

A11 = 1*(3+1) = 4

A12 = -1*(9+2) = -11

A13 = 1*1 = 1

A21 = -1*(-6) = 6

A22 = 1*(3-0) = 3

A23 = -1*(1+4) = -5

A31 = 1*2 = 2

A32 = -1*(-1) = -1

A33 = 1+(1+6) = 7

3. השלב הבא הוא להרכיב מטריצה ​​מהתוספות שהתקבלו:

5. הכפל את המטריצה ​​הזו בהיפוך של הקובע, כלומר ב-1/26:

6. עכשיו אנחנו רק צריכים לבדוק:

במהלך הבדיקה, קיבלנו מטריצת זהות, ולכן הפתרון בוצע בצורה נכונה לחלוטין.

2 דרכים לחשב את המטריצה ​​ההפוכה.

1. טרנספורמציה של מטריצה ​​אלמנטרית

2. מטריצה ​​הפוכה דרך ממיר אלמנטרי.

טרנספורמציה של מטריצה ​​יסודית כוללת:

1. הכפלת מחרוזת במספר שאינו שווה לאפס.

2. הוספת לכל שורה שורה נוספת כפול מספר.

3. החליפו את שורות המטריצה.

4. יישום שרשרת של טרנספורמציות יסודיות, נקבל מטריצה ​​נוספת.

א -1 = ?

1. (A|E) ~ (E|A -1 )

2.א -1 * A = E

בואו נסתכל על זה באמצעות דוגמה מעשית עם מספרים ממשיים.

תרגיל:מצא את המטריצה ​​ההפוכה.

פִּתָרוֹן:

בוא נבדוק:

הבהרה קטנה לגבי הפתרון:

ראשית, סידרנו מחדש את שורות 1 ו-2 של המטריצה, ואז הכפלנו את השורה הראשונה ב- (-1).

לאחר מכן, הכפלנו את השורה הראשונה ב-(-2) והוספנו אותה עם השורה השנייה של המטריצה. ואז הכפלנו את שורה 2 ב-1/4.

השלב האחרון של הטרנספורמציה היה הכפלת השורה השנייה ב-2 והוספתה עם הראשונה. כתוצאה מכך, יש לנו את מטריצת הזהות בצד שמאל, ולכן המטריצה ​​ההפוכה היא המטריצה ​​מימין.

לאחר בדיקה, השתכנענו שההחלטה נכונה.

כפי שאתה יכול לראות, חישוב המטריצה ​​ההפוכה הוא פשוט מאוד.

בסוף הרצאה זו, אני גם רוצה להקדיש מעט זמן למאפיינים של מטריצה ​​כזו.

בחלק הראשון, בדקנו כיצד למצוא את המטריצה ​​ההפוכה באמצעות תוספות אלגבריות. כאן נתאר שיטה נוספת למציאת מטריצות הפוכות: שימוש בתמורות גאוס וגאוס-ירדן. שיטה זו למציאת המטריצה ​​ההפוכה נקראת לעתים קרובות שיטת הטרנספורמציות היסודיות.

שיטת טרנספורמציה אלמנטרית

כדי ליישם שיטה זו, המטריצה ​​הנתונה $A$ ומטריצת הזהות $E$ נכתבות למטריצה ​​אחת, כלומר. יוצרים מטריצה ​​בצורה $(A|E)$ (מטריצה ​​זו נקראת גם מורחבת). לאחר מכן, בעזרת טרנספורמציות אלמנטריות המבוצעות עם שורות המטריצה ​​המורחבת, מובטח שהמטריקס משמאל לקו הופכת לזהות, והמטריצה ​​המורחבת לובשת את הצורה $\left(E| A^(- 1) \right)$. טרנספורמציות יסודיות במצב זה כוללות את הפעולות הבאות:

1. החלפת שני קווים.
2. הכפלת כל הרכיבים של מחרוזת במספר כלשהו שאינו שווה לאפס.
3. הוספת לאלמנטים של שורה אחת את האלמנטים המתאימים של שורה אחרת, כפול גורם כלשהו.

ניתן ליישם את התמורות היסודיות הללו בדרכים שונות. בדרך כלל בוחרים בשיטת גאוס או בשיטת גאוס-ירדן. באופן כללי, שיטות גאוס וגאוס-ירדן מיועדות לפתרון מערכות של משוואות אלגבריות ליניאריות, ולא למציאת מטריצות הפוכות. יש להבין כאן את הביטוי "שימוש בשיטת גאוס למציאת המטריצה ​​ההפוכה" כ"שימוש בפעולות הגלומות בשיטה גאוסית כדי למצוא את המטריצה ​​ההפוכה".

מספור הדוגמאות ממשיך מהחלק הראשון. הדוגמאות דנות בשימוש בשיטת גאוס למציאת המטריצה ​​ההפוכה, והדוגמאות דנות בשימוש בשיטת גאוס-ירדן. יש לציין שאם במהלך הפתרון כל האלמנטים של שורה או עמודה מסוימת של המטריצה ​​הממוקמים לפני הקו מאופסים לאפס, אז המטריצה ​​ההפוכה לא קיימת.

דוגמה מס' 5

מצא את המטריצה ​​$A^(-1)$ אם $A=\left(\begin(array) (ccc) 7 & 4 & 6 \\ 2 & 5 & -4 \\ 1 & -1 & 3 \end( מערך) \right)$.

בדוגמה זו, המטריצה ​​ההפוכה תימצא בשיטת גאוס. המטריצה ​​המורחבת, שבאופן כללי היא בעלת הצורה $(A|E)$, בדוגמה זו תקבל את הצורה הבאה: $ \left(\begin(array) (ccc|ccc) 7 & 4 & 6 & 1 & 0 & 0 \\ 2 & 5 & -4 & 0 & 1 & 0 \\ 1 & -1 & 3 & 0 & 0 & 1 \end(array) \right)$.

מטרה: באמצעות טרנספורמציות יסודיות, הבא את המטריצה ​​המורחבת לצורה $\left(E|A^(-1) \right)$. הבה ניישם את אותן פעולות המשמשות בעת פתרון מערכות של משוואות ליניאריות בשיטת גאוס. ליישם את שיטת גאוס, זה נוח כאשר האלמנט הראשון בשורה הראשונה של המטריצה ​​המורחבת הוא אחד. כדי להשיג זאת, אנו מחליפים את השורה הראשונה והשלישית של המטריצה ​​המורחבת, אשר הופכת: $ \left(\begin(array) (ccc|ccc) 1 & -1 & 3 & 0 & 0 & 1 \\ 2 & 5 & - 4 & 0 & 1 & 0 \\ 7 & 4 & 6 & 1 & 0 & 0 \end(array) \right)$.

עכשיו בואו נגיע לפתרון. שיטת גאוס מחולקת לשני שלבים: קדימה ואחורה (תיאור מפורט של שיטה זו לפתרון מערכות משוואות ניתן בדוגמאות של הנושא המקביל). אותם שני שלבים יחולו בתהליך מציאת המטריצה ​​ההפוכה.

שבץ ישר

צעד ראשון

באמצעות השורה הראשונה, אנו מאפסים את הרכיבים של העמודה הראשונה הממוקמת מתחת לשורה הראשונה:

הרשו לי להגיב מעט על הפעולה שבוצעה. הסימן $II-2\cdot I$ פירושו שהרכיבים התואמים של השורה הראשונה, שהוכפלו קודם לכן בשתיים, הופחתו מהאלמנטים של השורה השנייה. פעולה זו יכולה להיכתב בנפרד באופן הבא:

הפעולה $III-7\cdot I$ מתבצעת בדיוק באותו אופן. אם יש קשיים בביצוע פעולות אלו, ניתן לבצע אותן בנפרד (בדומה לפעולה $II-2\cdot I$ המופיעה למעלה), ולאחר מכן ניתן להזין את התוצאה לתוך המטריצה ​​המורחבת.

צעד שני

באמצעות השורה השנייה, אנו מאפסים את האלמנט של העמודה השנייה הממוקמת מתחת לשורה השנייה:

מחלקים את השורה השלישית ב-5:

המהלך הישיר הסתיים. כל האלמנטים הממוקמים מתחת לאלכסון הראשי של המטריצה ​​עד לקו מאופסים לאפס.

מהלך הפוך

צעד ראשון

באמצעות השורה השלישית, אנו מאפסים את הרכיבים של העמודה השלישית הממוקמת מעל השורה השלישית:

לפני שנמשיך לשלב הבא, בואו נחלק את השורה השנייה ב-$7$:

צעד שני

באמצעות השורה השנייה, אנו מאפסים את הרכיבים של העמודה השנייה הממוקמת מעל השורה השנייה:

הטרנספורמציות הושלמו, המטריצה ​​ההפוכה נמצאת בשיטת גאוס: $A^(-1)=\left(\begin(array) (ccc) -11/5 & 18/5 & 46/5 \\ 2 & -3 & -8 \ \7/5 & -11/5 & -27/5 \end(מערך) \right)$. הבדיקה, במידת הצורך, יכולה להתבצע באותו אופן כמו בדוגמאות הקודמות. אם תדלג על כל ההסברים, הפתרון ייראה כך:

תשובה: $A^(-1)=\left(\begin(array) (ccc) -11/5 & 18/5 & 46/5 \\ 2 & -3 & -8 \\ 7/5 & -11/ 5 ו-27/5 \end(מערך) \right)$.

דוגמה מס' 6

מצא את המטריצה ​​$A^(-1)$ אם $A=\left(\begin(array) (cccc) -5 & 4 & 1 & 0 \\ 2 & 3 & -2 & 1 \\ 0 & 7 & -4 & -3 \\ 1 & 4 & 0 & 6 \end(מערך) \right)$.

כדי למצוא את המטריצה ​​ההפוכה בדוגמה זו, נשתמש באותן פעולות המשמשות בעת פתרון מערכות של משוואות לינאריות בשיטת גאוס. הסברים מפורטים מובאים, אך כאן נצמצם להערות קצרות. בוא נכתוב את המטריצה ​​המורחבת: $\left(\begin(array) (cccc|cccc) -5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \\ 2 & 3 & -2 & 1 &0 &1&0 &0 \ \ 0 & 7 & -4 & -3 &0 & 0 & 1 & 0\\ 1 & 4 & 0 & 6 &0 &0 & 0 & 1 \end(array) \right)$. בואו נחליף את השורה הראשונה והרביעית של המטריצה ​​הזו: $\left(\begin(array) (cccc|cccc) 1 & 4 & 0 & 6 &0 &0 & 0 & 1 \\ 2 & 3 & -2 & 1 &0 &1&0 &0 \ \0 & 7 & -4 & -3 &0 & 0 & 1 & 0\\ -5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \end(array) \right)$.

שבץ ישר

המרות קדימה הושלמו. כל האלמנטים הממוקמים מתחת לאלכסון הראשי של המטריצה ​​משמאל לקו מאופסים לאפס.

מהלך הפוך

המטריצה ​​ההפוכה נמצאה בשיטת גאוס, $A^(-1)=\left(\begin(array) (cccc) -13/14 & -75/8 & 31/8 & 7/2 \\ -19 /8 & - 117/16 & 49/16 & 11/4 \\ -23/4 & -141/8 & 57/8 & 13/2 \\ 17/8 & 103/6 & -43/16 & - 9/4 \ end(array)\right)$. במידת הצורך, אנו מבצעים את הבדיקה באותו אופן כמו בדוגמאות מס' 2 ו-3.

תשובה: $A^(-1)=\left(\begin(array) (cccc) -13/14 & -75/8 & 31/8 & 7/2 \\ -19/8 & -117/16 & 49 /16 & 11/4 \\ -23/4 & -141/8 & 57/8 & 13/2 \\ 17/8 & 103/6 & -43/16 & -9/4 \end(array) \ נכון)$.

דוגמה מס' 7

מצא את המטריצה ​​$A^(-1)$ אם $A=\left(\begin(array) (ccc) 2 & 3 & 4 \\ 7 & 1 & 9 \\ -4 & 5 & -2 \end( מערך) \right)$.

כדי למצוא את המטריצה ​​ההפוכה, אנו מיישמים פעולות האופייניות לשיטת גאוס-ירדן. ההבדל משיטת גאוס, שנידון בדוגמאות קודמות וכן, הוא שהפתרון מתבצע בשלב אחד. הרשו לי להזכיר לכם ששיטת גאוס מחולקת ל-2 שלבים: המהלך קדימה ("אנחנו עושים" אפסים מתחת לאלכסון הראשי של המטריצה ​​לקו) והמהלך ההפוך (אנחנו מאפסים את האלמנטים מעל האלכסון הראשי של המטריצה לקו). כדי לחשב את המטריצה ​​ההפוכה בשיטת גאוס-ירדן, אין צורך בשני שלבי פתרון. ראשית, בואו ניצור מטריצה ​​מורחבת: $(A|E)$:

$$ (A|E)=\left(\begin(array) (ccc|ccc) 2 & 3 & 4 & 1 & 0 & 0\\ 7 & 1 & 9 & 0 & 1 & 0\\ -4 & 5 & ​​-2 & 0 & 0 & 1 \end(מערך) \right) $$

צעד ראשון

הבה נאפס את כל הרכיבים של העמודה הראשונה מלבד אחד. בעמודה הראשונה, כל האלמנטים אינם אפס, כך שאנו יכולים לבחור כל אלמנט. ניקח לדוגמא $(-4)$:

האלמנט שנבחר $(-4)$ נמצא בשורה השלישית, לכן אנו משתמשים בשורה השלישית כדי לאפס את האלמנטים שנבחרו בעמודה הראשונה:

בואו נעשה את האלמנט הראשון בשורה השלישית שווה לאחד. כדי לעשות זאת, חלקו את האלמנטים של השורה השלישית של המטריצה ​​המורחבת ב-$(-4)$:

כעת נמשיך לאפס את האלמנטים המתאימים של העמודה הראשונה:

בשלבים נוספים לא ניתן יהיה להשתמש יותר בשורה השלישית, כי כבר השתמשנו בה בשלב הראשון.

צעד שני

בוא נבחר אלמנט מסוים שאינו אפס של העמודה השנייה ונאפס את כל שאר האלמנטים של העמודה השנייה לאפס. אנו יכולים לבחור אחד משני אלמנטים: $\frac(11)(2)$ או $\frac(39)(4)$. לא ניתן לבחור את האלמנט $\left(-\frac(5)(4) \right)$, מכיוון שהוא ממוקם בשורה השלישית, בה השתמשנו בשלב הקודם. בוא נבחר את האלמנט $\frac(11)(2)$, שנמצא בשורה הראשונה. בואו נוודא שבמקום $\frac(11)(2)$ בשורה הראשונה יש אחד:

כעת נאפס את האלמנטים המתאימים של העמודה השנייה:

לא ניתן להשתמש בשורה הראשונה בדיונים נוספים.

צעד שלישי

עלינו לאפס את כל הרכיבים של העמודה השלישית מלבד אחד. עלינו לבחור אלמנט שאינו אפס בעמודה השלישית. עם זאת, אנחנו לא יכולים לקחת $\frac(6)(11)$ או $\frac(13)(11)$ מכיוון שהאלמנטים האלה ממוקמים בשורה הראשונה והשלישית שבה השתמשנו קודם לכן. הבחירה קטנה: נשאר רק האלמנט $\frac(2)(11)$, שנמצא בשורה השנייה. בואו נחלק את כל הרכיבים של השורה השנייה ב-$\frac(2)(11)$:

כעת נאפס את האלמנטים המתאימים של העמודה השלישית:

הושלמו טרנספורמציות בשיטת גאוס-ירדן. כל מה שנותר הוא לוודא שהמטריקס הופך ליחידה עד לקו. לשם כך תצטרך לשנות את סדר השורות. ראשית, הבה נחליף את השורה הראשונה והשלישית:

$$ \left(\begin(array) (ccc|ccc) 1 & 0 & 0 & 47/4 & -13/2 & -23/4 \\ 0 & 0 & 1 & -39/4 & 11/2 & 19/4 \\ 0 & 1 & 0 & 11/2 & -3 & -5/2 \end(מערך) \right) $$

כעת נחליף את השורה השנייה והשלישית:

$$ \left(\begin(array) (ccc|ccc) 1 & 0 & 0 & 47/4 & -13/2 & -23/4 \\ 0 & 1 & 0 & 11/2 & -3 & - 5/2 \\ 0 & 0 & 1 & -39/4 & 11/2 & 19/4 \end(מערך) \right) $$

אז, $A^(-1)=\left(\begin(array) (ccc) 47/4 & -13/2 & -23/4 \\ 11/2 & -3 & -5/2 \\ - 39/4 & 11/2 & 19/4 \end(מערך) \right)$. מטבע הדברים, הפתרון יכול להתבצע בצורה שונה, בבחירת אלמנטים הממוקמים באלכסון הראשי. זה בדרך כלל מה שהם עושים, כי במקרה הזה, בסוף הפתרון, אין צורך להחליף קווים. את הפתרון הקודם נתתי רק למטרה אחת: להראות שבחירת הקו בכל שלב אינה חשובה. אם תבחר אלמנטים אלכסוניים בכל שלב, הפתרון ייראה כך.

מציאת המטריצה ​​ההפוכה- בעיה שנפתרת לרוב בשתי שיטות:

• שיטת התוספות האלגבריות, הדורשת מציאת דטרמיננטים והעברה של מטריצות;
• שיטת גאוס לחיסול אלמונים, הדורשת ביצוע טרנספורמציות יסודיות של מטריצות (הוספת שורות, הכפלת שורות באותו מספר וכו').

למי שסקרן במיוחד, ישנן שיטות נוספות, למשל שיטת הטרנספורמציות ליניאריות. בשיעור זה ננתח את שלושת השיטות והאלגוריתמים שהוזכרו למציאת המטריצה ​​ההפוכה באמצעות שיטות אלו.

מטריצה ​​הפוכה א, מטריצה ​​כזו נקראת

א
. (1)

מטריצה ​​הפוכה , שצריך למצוא עבור מטריצה ​​מרובעת נתונה א, מטריצה ​​כזו נקראת

התוצר ממנו המטריצות אבצד ימין נמצאת מטריצת הזהות, כלומר.
. (1)

מטריצת זהות היא מטריצה ​​אלכסונית שבה כל האלמנטים האלכסוניים שווים לאחד.

מִשׁפָּט.לכל מטריצה ​​ריבועית לא יחידה (לא מנוונת, לא יחידה), אפשר למצוא מטריצה ​​הפוכה, ורק אחת. עבור מטריצה ​​מרובעת מיוחדת (מנוונת, יחידה), המטריצה ​​ההפוכה אינה קיימת.

המטריצה ​​הריבועית נקראת לא מיוחד(אוֹ לא מנוון, לא יחיד), אם הקובע שלו אינו אפס, ו מיוחד(אוֹ דֵגֵנֵרָט, יָחִיד) אם הקובע שלו הוא אפס.

ניתן למצוא את היפוך של מטריצה ​​רק עבור מטריצה ​​מרובעת. באופן טבעי, גם המטריצה ​​ההפוכה תהיה מרובעת ובאותו סדר כמו המטריצה ​​הנתונה. מטריצה ​​שעבורה ניתן למצוא מטריצה ​​הפוכה נקראת מטריצה ​​הפיכה.

ל מטריצה ​​הפוכה יש אנלוגיה רלוונטית להיפוך של מספר. לכל מספר א, לא שווה לאפס, יש מספר כזה בכי העבודה או בשווה לאחד: אב= 1 . מספר בנקרא היפוך של מספר ב. לדוגמה, עבור המספר 7 ההדדיות היא 1/7, שכן 7*1/7=1.

מציאת המטריצה ​​ההפוכה באמצעות שיטת התוספות אלגבריות (מטריקס ברית)

למטריצה ​​מרובעת שאינה יחידה אההפוך הוא המטריצה

איפה הקובע של המטריצה א, a היא מטריצה ​​הקשורה למטריצה א.

ברית עם מטריצה ​​מרובעת אהיא מטריצה ​​באותו סדר, שהרכיבים שלה הם המשלים האלגבריים של האלמנטים המקבילים של הקובע של המטריצה ​​המוטרפים ביחס למטריצה ​​A. לפיכך, אם

זֶה

ו

אלגוריתם למציאת המטריצה ​​ההפוכה בשיטת התוספות אלגבריות

1. מצא את הקובע של מטריצה ​​זו א. אם הקובע שווה לאפס, מציאת המטריצה ​​ההפוכה נעצרת, שכן המטריצה ​​היא יחידה וההפוך שלה לא קיים.

2. מצא את המטריצה ​​המוטרפת ביחס ל א.

3. חשב את המרכיבים של מטריצת האיחוד כהשלמה אלגברית של המאריץ שנמצא בשלב 2.

4. החל נוסחה (2): הכפלו את ההפך של הקובע המטריצה א, למטריצת האיחוד שנמצאה בשלב 4.

5. בדוק את התוצאה שהתקבלה בשלב 4 על ידי הכפלת מטריצה ​​זו אלמטריצה ​​ההפוכה. אם המכפלה של מטריצות אלו שווה למטריצת הזהות, אז המטריצה ​​ההפוכה נמצאה בצורה נכונה. אחרת, התחל שוב את תהליך הפתרון.

דוגמה 1.למטריצה

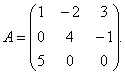
מצא את המטריצה ​​ההפוכה.

פִּתָרוֹן. כדי למצוא את המטריצה ​​ההפוכה, עליך למצוא את הקובע של המטריצה א. אנו מוצאים לפי כלל המשולשים:

לכן, המטריצה א– לא יחיד (לא מנוון, לא יחיד) ויש לזה הפוך.

בואו נמצא מטריצה ​​הקשורה למטריצה ​​הזו א.

הבה נמצא את המטריצה ​​המוטרפת ביחס למטריצה א:

אנו מחשבים את האלמנטים של מטריצת הברית כהשלמות אלגבריות של המטריצה ​​שהועברו ביחס למטריצה א:

לכן, המטריצה ​​קשורה למטריצה א, יש את הצורה

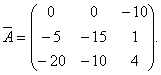
תגובה.הסדר שבו מחושבים האלמנטים והעברת המטריצה ​​עשוי להיות שונה. אתה יכול תחילה לחשב את המשלים האלגבריים של המטריצה א, ולאחר מכן תמיר את מטריצת המשלים האלגברי. התוצאה צריכה להיות אותם אלמנטים של מטריצת האיחוד.

ביישום נוסחה (2), נמצא את המטריצה ​​הפוכה למטריצה א:

מציאת המטריצה ​​ההפוכה באמצעות שיטת האלימינציה הלא ידועה של גאוס

הצעד הראשון למציאת היפוך של מטריצה ​​באמצעות שיטת החיסול גאוס הוא להקצות למטריצה אמטריצת זהות מאותו סדר, המפרידה ביניהם עם פס אנכי. נקבל מטריצה ​​כפולה. בוא נכפיל את שני הצדדים של המטריצה ​​הזו ב-, ואז נקבל

,

אלגוריתם למציאת המטריצה ​​ההפוכה בשיטת האלימינציה הלא ידועה של גאוס

1. אל המטריצה אלהקצות מטריצת זהות באותו סדר.

2. הפוך את המטריצה ​​הכפולה שנוצרה כך שבצד שמאל תקבל מטריצת יחידה, ואז בצד ימין, במקום מטריצת הזהות, תקבל אוטומטית מטריצה ​​הפוכה. מַטרִיצָה אבצד שמאל הופך למטריצת הזהות על ידי טרנספורמציות מטריצות יסודיות.

2. אם בתהליך של טרנספורמציה מטריצה אבמטריצת הזהות יהיו רק אפסים בכל שורה או בכל עמודה, ואז הקובע של המטריצה ​​שווה לאפס, וכתוצאה מכך, המטריצה איהיה יחיד, ואין לו מטריצה ​​הפוכה. במקרה זה, קביעה נוספת של המטריצה ​​ההפוכה נעצרת.

דוגמה 2.למטריצה

מצא את המטריצה ​​ההפוכה.

ונהפוך אותו כך שבצד שמאל נקבל מטריצת זהות. אנחנו מתחילים את השינוי.

מכפילים את השורה הראשונה של המטריצה ​​השמאלית והימנית ב- (-3) ומוסיפים אותה לשורה השנייה, ואז נכפיל את השורה הראשונה ב- (-4) ונוסיף אותה לשורה השלישית, ואז נקבל

.

כדי להבטיח שאין מספרים שברים בהמרה הבאה, הבה ניצור תחילה יחידה בשורה השנייה בצד שמאל של המטריצה ​​הכפולה. כדי לעשות זאת, נכפיל את השורה השנייה ב-2 ונחסיר ממנה את השורה השלישית, ואז נקבל

.

בוא נוסיף את השורה הראשונה עם השניה, ואז נכפיל את השורה השנייה ב-(-9) ונוסיף אותה עם השורה השלישית. ואז אנחנו מקבלים

.

לאחר מכן חלקו את השורה השלישית ב-8

.

הכפלו את השורה השלישית ב-2 והוסיפו אותה לשורה השנייה. מתברר:

.

בואו נחליף את השורה השנייה והשלישית, ואז סוף סוף נקבל:

.

אנו רואים שבצד שמאל יש לנו את מטריצת הזהות, לכן, בצד ימין יש לנו את המטריצה ​​ההפוכה. לכן:

.

אתה יכול לבדוק את נכונות החישובים על ידי הכפלת המטריצה ​​המקורית במטריצה ​​ההפוכה שנמצאה:

התוצאה צריכה להיות מטריצה ​​הפוכה.

דוגמה 3.למטריצה

מצא את המטריצה ​​ההפוכה.

פִּתָרוֹן. הידור מטריצה ​​כפולה

ואנחנו נשנה אותו.

נכפיל את השורה הראשונה ב-3, ואת השניה ב-2, ונחסיר מהשורה השנייה, ואז נכפיל את השורה הראשונה ב-5, ואת השלישית ב-2 ונחסיר מהשורה השלישית, ואז נקבל

.

נכפיל את השורה הראשונה ב-2 ונוסיף אותה לשניה, ואז נחסר את השני מהשורה השלישית, ואז נקבל

.

אנו רואים שבשורה השלישית בצד שמאל כל האלמנטים שווים לאפס. לכן, המטריצה ​​היא יחידה ואין לה מטריצה ​​הפוכה. אנחנו מפסיקים עוד למצוא את מריץ ההפוך.