Pickov vzorec

1. Úvod

2. Peakov vzorec. Ukážka I.

Dôkaz II.

Dôkaz Sh.

3. Ciele.

4. Vzorec pre oblasť mnohouholníka pomocou súradníc vrcholov.

5. Úlohy.

6. Literatúra

Peakov vzorec.

1. Úvod.

Múdrosť čerpáme z histórie,

v poézii - vtip,

v matematike - vhľad.

F. Bacon

Dej sa bude odvíjať na obyčajnom károvanom papieri.

Čiary prebiehajúce po stranách buniek tvoria mriežku a vrcholy buniek sú uzlami tejto mriežky. Nakreslíme na list mnohouholník s vrcholmi v uzloch a nájdeme jeho plochu.

Môžete ho hľadať rôznymi spôsobmi. Môžete napríklad rozrezať mnohouholník na pomerne jednoduché tvary, nájsť ich oblasti a sčítať ich.

Tu nás však čaká veľa problémov. Obrázok sa dá ľahko rozdeliť na obdĺžniky, lichobežníky a trojuholníky a jeho plocha sa vypočíta bez námahy.

Hoci polygón vyzerá dostatočne jednoducho, výpočet jeho plochy si vyžaduje veľa práce. Čo keby polygón vyzeral elegantnejšie? Ukazuje sa, že oblasti polygónov, ktorých vrcholy sa nachádzajú v uzloch mriežky, sa dajú vypočítať oveľa jednoduchšie: existuje vzorec, ktorý spája ich plochu s počtom uzlov ležiacich vo vnútri a na hranici mnohouholníka. Tento úžasný a jednoduchý vzorec sa nazýva Pick vzorec.

2. Peakov vzorec.

Vrcholy mnohouholníka (nie nevyhnutne konvexné) sa nachádzajú v uzloch celočíselnej mriežky. Vo vnútri sa nachádzajú uzly mriežky B a na hranici sú uzly G. Dokážme, že jeho plocha sa rovná B + – 1 (Vyberte vzorec).

Ukážka I.

Uvažujme polygón, ktorého vrcholy sa nachádzajú v uzloch celočíselnej mriežky, to znamená, že majú celočíselné súradnice.

Mnohouholník rozdeľujeme na trojuholníky s vrcholmi v uzloch mriežky, ktoré neobsahujú žiadne uzly ani vo vnútri, ani na stranách.

Označme:

n– počet strán mnohouholníka,

m– počet trojuholníkov s vrcholmi v uzloch mriežky, ktoré neobsahujú uzly ani vo vnútri, ani na stranách,

B – počet uzlov vo vnútri polygónu,

Г – počet uzlov na stranách vrátane vrcholov.

Plochy všetkých týchto trojuholníkov sú rovnaké a rovnaké.

Preto je plocha polygónu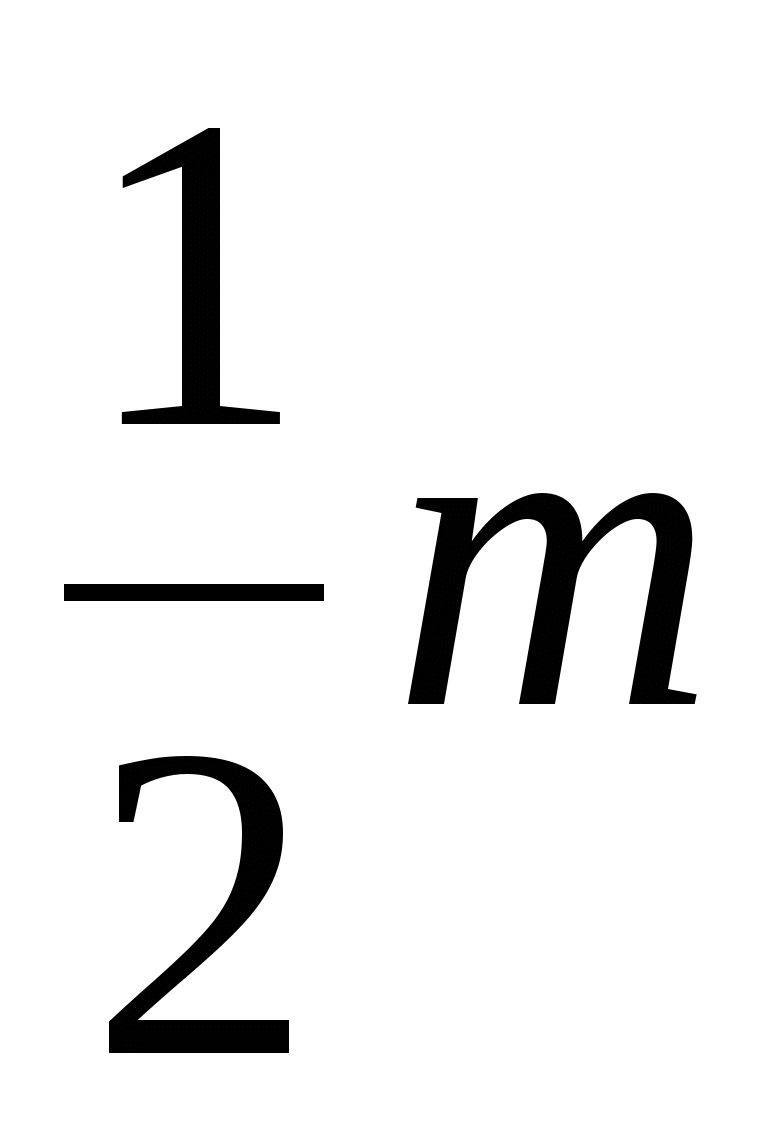
.

180 0 m .

Teraz zistime túto sumu iným spôsobom.

Súčet uhlov s vrcholom v akomkoľvek vnútornom uzle je 360 ​​0.

Potom sa súčet uhlov s vrcholmi vo všetkých vnútorných uzloch rovná 360 0 V.

Celkový súčet uhlov pre uzly na stranách, ale nie na vrcholoch, je 180 0 (G - n).

Súčet uhlov vo vrcholoch mnohouholníka je 180 0 ( n – 2) .

Celkový súčet uhlov všetkých trojuholníkov je 360 0 V + 180 0 (G – n) + 180 0 (n – 2).

Takže 1800 m= 360 0 V + 180 0 (G – n) + 180 0 (n – 2),

180 0 m= 360 0 V + 180 0 G – 180 0 n + 180 0 n– 180 0 2,

180 0 m= 360 0 V + 180 0 G – 360 0,

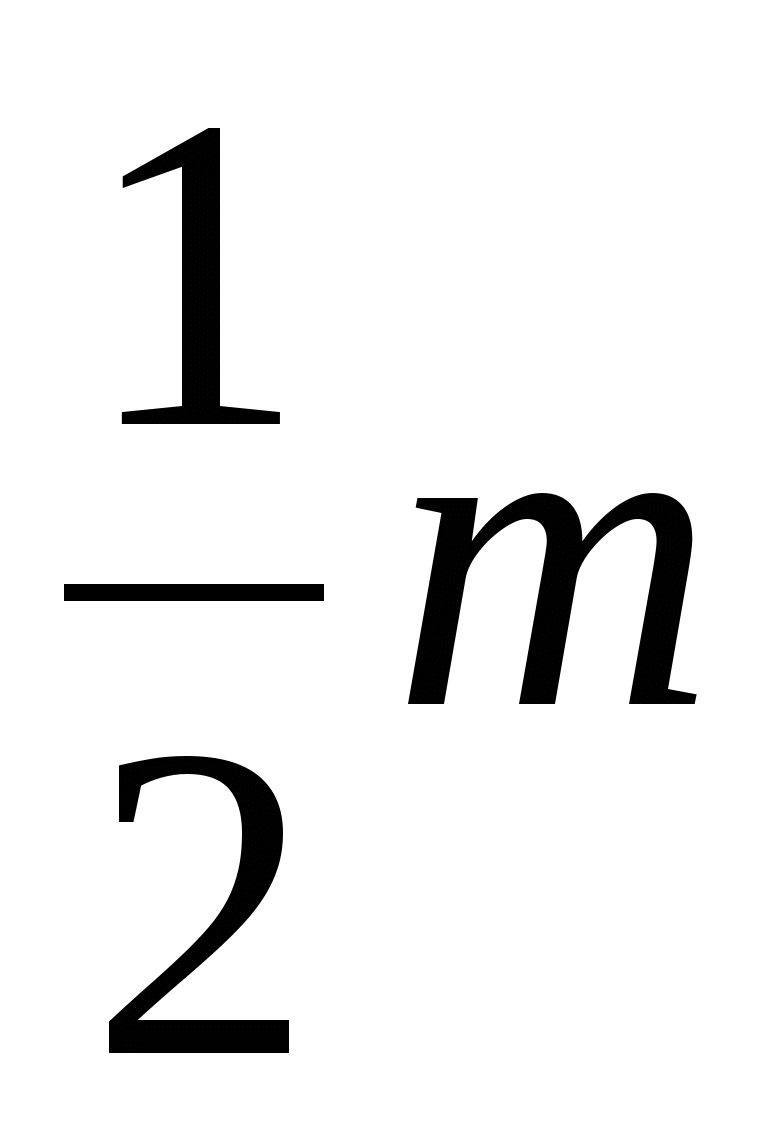= B+ – 1 ,

z ktorého získame výraz pre oblasť S mnohouholníka:

S= B+ – 1 ,

známy ako Pickov vzorec.

Na obrázku: B = 24, D = 9, tedaS = 24 + – 1 = 27,5.

Nájdite oblasť prvého mnohouholníka pomocou Peakovho vzorca:

B = 28 (zelené bodky);

G = 20 (modré bodky).

Dostávame, S =
= 37 štvorcových jednotiek

Dôkaz II.

Každému polygónu M s vrcholmi v uzloch celočíselnej mriežky priradíme číslo f (M) =
, kde sa sčítanie vykonáva cez všetky uzly mriežky patriace do M a uhol je definovaný nasledovne: =
pre vnútorný bod mnohouholníka, =
pre hraničný bod iný ako vrchol a – vrcholový uhol, ak je tento uzol vrcholom. Je ľahké vidieť, že f(M) =
+
= B+ – 1. Zostáva skontrolovať, či sa číslo f (M) rovná ploche mnohouholníka M.

Nech je mnohouholník M rozrezaný na mnohouholníky M 1 a M 2 s vrcholmi v uzloch mriežky. Potom f (M) = f (M 1) + f (M 2), keďže pre každý uzol sa uhly sčítajú. Ak teda Pickov vzorec platí pre dva z polygónov M, M 1 a M 2, platí to aj pre tretí.

Ak M je obdĺžnik so stranami p A q, smerované pozdĺž mriežkových línií, potom

f (M) = (p – 1) (q – 1) +
= pq.

V tomto prípade platí Peakov vzorec. Rozrezaním obdĺžnika M s uhlopriečkou na trojuholníky M 1 a M 2 a využitím skutočnosti, že f (M) = f (M 1) + f (M 2) a f (M 1) = f (M 2), je ľahké dokázať platnosť Pickovho vzorca pre akýkoľvek pravouhlý trojuholník s nohami nasmerovanými pozdĺž čiar mriežky. Vyrezaním niekoľkých z týchto trojuholníkov z obdĺžnika môžete získať ľubovoľný trojuholník.

Na dokončenie dôkazu Pickovho vzorca zostáva poznamenať, že ľubovoľný mnohouholník môže byť rozdelený na trojuholníky pomocou nesúvislých uhlopriečok.

Dôkaz Sh.

Vzťah medzi plochou obrázku a počtom uzlov zahrnutých na tomto obrázku je obzvlášť jasne viditeľný v prípade obdĺžnika.

Nechaj ABCD- obdĺžnik s vrcholmi na uzloch a stranách prebiehajúcimi pozdĺž čiar mriežky.

Označme podľa IN počet uzlov ležiacich vo vnútri obdĺžnika a cez G- počet uzlov na jeho hranici. Posuňme mriežku o pol bunky doprava a o polovicu nadol.

Potom možno územie obdĺžnika „rozdeliť“ medzi uzly takto: každý z IN uzly „ovládajú“ celú bunku posunutej mriežky, každý z nich G– 4 hraničné nerohové uzly predstavujú polovicu bunky a každý z rohových bodov predstavuje štvrtinu bunky. Preto sa plocha obdĺžnika S rovná

Takže pre obdĺžniky s vrcholmi v uzloch a na stranách pozdĺž čiar mriežky sme vytvorili vzorec

Dokážme, že tento vzorec platí nielen pre obdĺžniky, ale aj pre ľubovoľné polygóny s vrcholmi v uzloch siete.

Označme podľa S m oblasť polygónuM s vrcholmi v uzloch a cezP m - veľkosť
, KdeIN m – počet uzlov vo vnútriM, A G m - počet uzlov na hranici. Potom Peakov vzorec možno zapísať ako
.

Dôkaz vzorca rozdelíme do niekoľkých krokov.

Krok 1

Ak polygónM s vrcholmi v uzloch siete rozrezanými na 2 polygónyM 1 A M 2 , majú tiež vrcholy iba v uzloch mriežky
. Nechajte polygónM rozrezané na mnohouholníkyM 1 A M 2 s vrcholmi v uzloch po segmente AB. Všetky uzly okrem tých, ktoré spadajú do segmentuAB, vykonajte rovnaké príspevky na ľavú a pravú stranu vzorca. Uvažujme uzly ležiace na segmente AB.

Ak takýto uzol leží medzi A a B (napríklad C), potom pre mnohouholníkM je vnútorný a pre mnohouholníkyM 1 A M 2 – hraničný. Preto jeho príspevok kP m sa rovná 1 a v každom z výrazov
A
– 0,5 každý, to znamená príspevky takéhoto uzla doP m A
sú si rovní.

Uvažujme uzly A a B. Sú to hraničné uzly pre oba M a pre M 1 , M 2 .

Preto príspevok každého z týchto uzlov kP m rovná 0,5 palca
- jednotka. To znamená, že celkový príspevok uzlov A a B kP m sa rovná 1, čo je o 1 menej ako ich príspevok k
. Ale
, A.

Z celkového „príspevku“ všetkých uzlov P m 1 sa odpočítava a od
2 sa odpočíta a to kompenzuje rozdiel v príspevkoch uzlov A a B.

takže,
.

Krok 2

Ak polygón M s vrcholmi v uzloch siete rozrezanými na dva polygóny M 1 A M 2 (aj s vrcholmi v uzloch) a vzorec je správny pre niektoré dva z polygónov MM 1 , M 2 , potom to platí aj pre tretí polygón.

Nech je to napríklad pravda preM 1 A M 2 , to jest
. Potom (prvým krokom), ale (podľa prvý krok) posledný výraz sa rovnáP m , a rovnosť
a existuje vzorec Peak.

Krok 3.

Dokážme Peakov vzorec pre pravouhlý trojuholník s vrcholmi v uzloch mriežky a nohami ležiacimi na čiarach mriežky.

Trojuholník ABC postavte ho do obdĺžnika ABCD .

Pre obdĺžniky je Pickov vzorec správny: S ABCD = P ABCD . Podľa prvého kroku P ABCD = P ABC + P ACD , P ABC = P ACD , Takže P ABCD = 2P ABC . Ale S ABCD = 2 S ABC . Preto S ABC = P ABC .

Krok 4.

Pickov vzorec platí pre ľubovoľný trojuholník s vrcholmi v uzloch mriežky.

Po preskúmaní obrázku je ľahké pochopiť: každý takýto trojuholník možno získať „odrezaním“ z určitého obdĺžnika so stranami pozdĺž čiar mriežky, niekoľkých obdĺžnikov a pravouhlých trojuholníkov s nohami na čiarach mriežky. A keďže Pickov vzorec platí pre obdĺžniky a pravouhlé trojuholníky, potom (zapamätajte si krok 2) platí aj pre pôvodný trojuholník.

Dokázali sme, že ak je možné polygón rozrezať na trojuholníky s vrcholmi v uzloch mriežky, potom preň platí Peakov vzorec.

3. Ciele.

Nájdite oblasť figúr:

1
.

B = 9

G = 4

B = 9

G = 5

Mnohouholník bez sebapriesečníkov sa nazýva mriežka, ak sa všetky jeho vrcholy nachádzajú v bodoch s celočíselnými súradnicami (v karteziánskom súradnicovom systéme).

Pickova veta

Vzorec

Dostaňme nejaký mriežkový polygón s nenulovou plochou.

Označme jej plochu ; počet bodov s celočíselnými súradnicami ležiacimi presne vo vnútri polygónu; počet bodov s celočíselnými súradnicami ležiacimi po stranách polygónu.

Potom sa ozval vzťah Pickov vzorec:

Najmä, ak sú hodnoty I a B známe pre určitý polygón, potom sa jeho plocha môže vypočítať ako , a to aj bez znalosti súradníc jeho vrcholov.

Tento vzťah objavil a dokázal rakúsky matematik Georg Alexander Pick v roku 1899.

Dôkaz

Dôkaz sa vykonáva v niekoľkých fázach: od najjednoduchších obrázkov po ľubovoľné polygóny:

Zovšeobecnenie do vyšších dimenzií

Bohužiaľ, tento jednoduchý a krásny Peake vzorec sa nedá dobre zovšeobecniť do vyšších dimenzií.

To jasne demonštroval Reeve, ktorý v roku 1957 navrhol zvážiť štvorsten (teraz tzv Reeve štvorsten) s nasledujúcimi vrcholmi:

kde je akékoľvek prirodzené číslo. Potom tento štvorsten neobsahuje jediný bod s celočíselnými súradnicami vo vnútri a na jeho hranici sú iba štyri body , , , a žiadne ďalšie. Objem a povrch tohto štvorstenu sa teda môžu líšiť, zatiaľ čo počet bodov vo vnútri a na hranici sa nemení; preto Pickov vzorec neumožňuje zovšeobecnenia ani na trojrozmerný prípad.

Napriek tomu stále existuje nejaké podobné zovšeobecnenie na priestory vyšších dimenzií – toto Ehrhartove polynómy(Ehrhartov polynóm), ale sú veľmi zložité a závisia nielen od počtu bodov vo vnútri a od hranice obrazca.

Na odhadnutie plochy mnohouholníka na kockovanom papieri stačí spočítať, koľko buniek tento mnohouholník pokrýva (plochu bunky berieme ako jednu). Presnejšie, ak S- oblasť mnohouholníka, - počet buniek, ktoré ležia úplne vo vnútri mnohouholníka a - počet buniek, ktoré majú aspoň jeden spoločný bod s vnútrom mnohouholníka.

Nižšie budeme brať do úvahy iba také polygóny, ktorých všetky vrcholy ležia v uzloch kockovaného papiera - v tých, kde sa pretínajú čiary mriežky. Ukazuje sa, že pre takéto polygóny je možné zadať nasledujúci vzorec:

kde je oblasť, r- počet uzlov, ktoré ležia striktne vo vnútri mnohouholníka.

Tento vzorec sa nazýva „Pick vzorec“ - podľa matematika, ktorý ho objavil v roku 1899.

Jednoduché trojuholníky

Plochu akéhokoľvek trojuholníka nakresleného na kockovanom papieri možno ľahko vypočítať tak, že ho predstavíte ako súčet alebo rozdiel plôch pravouhlých trojuholníkov a obdĺžnikov, ktorých strany sledujú čiary mriežky prechádzajúce cez vrcholy nakresleného trojuholníka. Keď to urobíte, napríklad pre trojuholníky zobrazené na obrázku 1.34, môžete sa uistiť, že oblasť sa vždy rovná „prijatému“ číslu - číslu formulára, kde je celé číslo.

Nazvime trojuholník jednoduchým, ak v ňom alebo na jeho stranách nie sú žiadne uzly siete, s výnimkou jeho vrcholov. Všetky jednoduché trojuholníky na obr. 1,34 majú plochu. Uvidíme, že to nie je náhodné.

Úloha. Tri kobylky (tri body) v počiatočnom okamihu sedia na troch vrcholoch jednej bunky a potom začnú „preskakovať“: každý môže preskočiť jednu z ďalších dvoch, potom skončí v bode symetrickom relatívnej na svoje vlastné (obr. 1.35, jasne, že po ľubovoľnom počte takýchto skokov kobylky padnú do uzlov kockovaného papiera). V akých trojitých bodoch môžu kobylky po pár skokoch skončiť?

Nazvime trojuholník dosiahnuteľný, ak sa v jeho vrcholoch môžu súčasne objaviť tri kobylky, ktoré boli pôvodne v troch vrcholoch jednej bunky; skok nazveme transformáciou trojuholníka, ktorá spočíva v tom, že jeden z vrcholov ide do bodu, ktorý je symetrický vzhľadom na ktorýkoľvek z ďalších dvoch vrcholov (tieto dva vrcholy zostanú na svojom mieste).

Veta 1. Nasledujúce tri vlastnosti trojuholníkov s vrcholmi v uzloch kockovaného papiera sú navzájom ekvivalentné:

1) trojuholník má obsah,

2) trojuholník je jednoduchý,

3) trojuholník je dosiahnuteľný.

Zoznámime sa s nasledujúcimi vlastnosťami jednoduchého trojuholníka, ktoré vedú k platnosti tejto vety.

1. Plocha trojuholníka sa pri skákaní nemení.

2. Každý dosiahnuteľný trojuholník má plochu.

3. Ak dokončíte jednoduchý trojuholník ABC na rovnobežník ABCD, potom nebudú žiadne uzly (nepočítajúc vrcholy) ani vo vnútri, ani po stranách tohto rovnobežníka.

4. Z jednoduchého trojuholníka pri skákaní sa získa jednoduchý trojuholník.

5. Z jednoduchého trojuholníka je jeden z uhlov tupý alebo rovný (a druhý prípad je možný len pre trojuholník, ktorého tri vrcholy patria do jednej bunky; takýto jednoduchý trojuholník so stranami 1, 1 budeme nazývať minimálny.)

6. Z akéhokoľvek jednoduchého neminimálneho trojuholníka môžete jedným skokom získať trojuholník, ktorého najdlhšia strana je menšia ako najdlhšia strana pôvodného.

7. Akýkoľvek jednoduchý trojuholník je možné premeniť na minimálny konečným počtom skokov.

8. Akýkoľvek jednoduchý trojuholník je dosiahnuteľný.

9. Akýkoľvek jednoduchý trojuholník má obsah.

10. Akýkoľvek trojuholník je možné rozrezať na jednoduché.

11. Plocha akéhokoľvek trojuholníka je rovnaká a kedykoľvek je rozrezaný na prvočísla, ich počet je rovnaký m.

12. Akýkoľvek trojuholník plochy je jednoduchý.

13. Pre ľubovoľné dva uzly A A IN mriežky, na segmente, medzi ktorým nie sú žiadne ďalšie uzly, je uzol S taký, že trojuholník ABC- jednoduchý.

14. Uzol S v predchádzajúcej vlastnosti si môžete vždy vybrať tak, že uhol DIA bude tupý alebo rovný.

15. Šachovnicovú rovinu rozrežme na rovnaké rovnobežníky tak, aby všetky uzly boli vrcholmi rovnobežníkov. Potom je každý z trojuholníkov, do ktorých je jeden z týchto rovnobežníkov vyrezaný svojou uhlopriečkou, jednoduchý.

16. (Obrátený 15). Trojuholník ABC- jednoduchý vtedy a len vtedy, ak všetky možné trojuholníky získané z ABC paralelné preklady prenášajúce uzol A do rôznych mriežkových uzlov, navzájom sa neprekrývajú.

17. Ak je mriežka - uzly kockovaného papiera - rozdelená na štyri podmriežky s bunkami (obr. 1.36), potom vrcholy jednoduchého trojuholníka budú nevyhnutne spadať do troch rôznych podmriežok (všetky tri majú rôzne označenia).

Nasledujúce dve vlastnosti poskytujú odpoveď na problém troch kobyliek.

18. Tri kobylky môžu naraz zasiahnuť tie a len tie trojice bodov, ktoré slúžia ako vrcholy jednoduchého trojuholníka a majú rovnaké znamienko ako zodpovedajúce vrcholy počiatočného trojuholníka.

19. Dva kobylky môžu naraz zasiahnuť len tie páry uzlov zodpovedajúcich označení na segmente, medzi ktorým nie sú žiadne ďalšie uzly.

Polygónová triangulácia

Budeme uvažovať o konkrétnom type polygónov na kockovanom papieri, ktoré zodpovedajú hodnotám vo vzorci Pick. Ale z tohto konkrétneho prípadu môžete prejsť rovno k najvšeobecnejšiemu pomocou vety o rozrezaní ľubovoľného mnohouholníka na trojuholníky (kockovaný papier už nie je potrebný).

Nech je na rovine daný nejaký mnohouholník a nejaká konečná množina TO body ležiace vo vnútri mnohouholníka a na jeho hranici (a všetky vrcholy mnohouholníka patria do množiny TO).

Triangulácia s vrcholmi TO sa nazýva rozdelenie daného mnohouholníka na trojuholníky s vrcholmi v množine TO tak, že každý bod z TO slúži ako vrchol každého z tých triangulačných trojuholníkov, ku ktorým tento bod patrí (to znamená body z TO nespadajte dovnútra ani na strany trojuholníkov, obr. 1,37).

Veta 2. a) Akékoľvek n-trojuholník sa môže diagonálne rozrezať na trojuholníky a počet trojuholníkov bude rovnaký n- 2 (tento oddiel je triangulácia s vrcholmi vo vrcholoch n-gon).

b) Nech je vyznačená hranica mnohouholníka r body (vrátane všetkých vrcholov), vnútri - viac i bodov. Potom nasleduje triangulácia s vrcholmi v označených bodoch a počet trojuholníkov takejto triangulácie bude rovnaký.

Samozrejme, a) je špeciálny prípad b), kedy.

Platnosť tejto vety vyplýva z nasledujúcich tvrdení.

1) Z vrcholu najväčšieho uhla n-gon(), vždy môžete nakresliť uhlopriečku, ktorá leží úplne vo vnútri mnohouholníka.

2) Ak n-štvorec je rozrezaný diagonálne na r- štvorcový a q- choď teda.

3) Súčet uhlov n-gon sa rovná.

4) Akékoľvek n-trojuholník sa dá diagonálne rozrezať na trojuholníky.

5) Pre každý trojuholník, vo vnútri a na hranici ktorého je vyznačených niekoľko bodov (vrátane všetkých troch jeho vrcholov), existuje triangulácia s vrcholmi v označených bodoch.

6) To isté platí pre každého n- gon.

7) Počet triangulačných trojuholníkov sa rovná, kde i A r- počet vyznačených niekoľkých bodov, respektíve vo vnútri a na hranici polygónu. Zavolajme oddiel n-gon do niekoľkých polygónov je správne, ak každý vrchol jedného z polygónov oddielu slúži ako vrchol všetkých ostatných polygónov oddielu, do ktorého patrí. 8) Ak z vrcholov k-gony, na ktoré sú rozdelené správnym spôsobom n-gon, i vrcholy ležia vo vnútri a r- na hraniciach n-gon, potom množstvo k-gony sú rovnaké

9) Ak body roviny a úsečky s koncami v týchto bodoch tvoria mnohouholník, správne rozdelený na mnohouholníky, potom (obr. 1.38)

Z viet 1 a 2 vyplýva vrcholový vzorec:

1.5 Pytagorova veta o súčte plôch štvorcov postavených na stranách pravouhlého trojuholníka

Veta. Súčet plôch štvorcov postavených na stranách pravouhlého trojuholníka sa rovná ploche štvorca postaveného na prepone tohto trojuholníka. Nechaj ABC(obr. 1.39) je pravouhlý trojuholník, a BDEA, AFGE A BCKH- štvorce postavené na nohách a prepone; musíte dokázať, že súčet plôch prvých dvoch štvorcov sa rovná ploche tretieho štvorca.

Poďme uskutočniť Slnko. Potom štvorec BCKH bude rozdelená na dva obdĺžniky. Dokážme, že obdĺžnik BLMH rovná štvorcu BDEA, a obdĺžnik LCKM rovná štvorcu AFGC.

Nakreslíme pomocné čiary DC A AN. Zvážte trojuholníky DCB A ABH. Trojuholník DCB majúci základ BD, spoločný so štvorcovým BDEA, a výšku CN, rovná výške AB tento štvorec sa rovná polovici štvorca. Trojuholník AVN majúci základ VN, spoločné s obdĺžnikom BLMH, a výška AR, rovná výške B.L. tohto obdĺžnika, ktorého veľkosť sa rovná jeho polovici. Pri porovnaní týchto dvoch trojuholníkov medzi sebou zistíme, že majú BD = VA A BC = VN(ako strany štvorca);

navyše DCB = AVN, pretože každý z týchto uhlov pozostáva zo spoločnej časti - ABC a pravý uhol. Takže trojuholníky AVN A BCD sú si rovní. Z toho vyplýva, že obdĺžnik BLMN rovná štvorcu BDEA. Rovnakým spôsobom je dokázané, že obdĺžnik LGKM rovná štvorcu AFGC. Z toho vyplýva, že námestie VSKN rovná súčtu štvorcov BDEA A AFGC.

Výpočet plochy postavy.

Vyberte metódu

Práca študenta 5. triedy na MBOU SOŠ č.23 v Irkutsku

Balšuková Alexandra

Vedúci: Khodyreva T.G.

2014

Výpočet plochy postavy. Vyberte metódu

Predmet štúdia : problémy na kockovanom papieri

Predmet výskumu : úlohy na výpočet plochy mnohouholníka na kockovanom papieri, metódy a techniky ich riešenia.

Metódy výskumu : porovnávanie, zovšeobecňovanie, analógie, štúdium literatúry a internetových zdrojov, analýza informácií.

Účel štúdie:

vybrať hlavné, zaujímavé a zrozumiteľné informácie

Analyzujte a systematizujte prijaté informácie

Nájdite rôzne metódy a techniky riešenia problémov na kockovanom papieri

kontrolné vzorce na výpočet plôch geometrických útvarov pomocou Pickovho vzorca

Vytvorte elektronickú prezentáciu práce na prezentáciu zozbieraného materiálu

Geometria je najmocnejším prostriedkom na zostrenie našich mentálnych schopností a umožňuje nám správne myslieť a uvažovať.

(G. Galileo)

Relevantnosť témy

Vášeň pre matematiku často začína premýšľaním o probléme. Takže pri štúdiu témy „Oblasť polygónov“ vyvstáva otázka, či existujú problémy, ktoré sa líšia od problémov, o ktorých sa hovorí v učebnici. Medzi takéto problémy patria problémy na kockovanom papieri. Aká je zvláštnosť takýchto problémov, existujú špeciálne metódy a techniky na riešenie problémov na kockovanom papieri. Na hodine matematiky nám učiteľ predstavil zaujímavú metódu výpočtu mnohouholníkov. Začal som študovať literatúru a internetové zdroje na túto tému. Zdalo by sa, že na kockovanej rovine, teda na nekonečnom papieri zoradenom do rovnakých štvorcov, sa dá nájsť niečo fascinujúce. Ukazuje sa, že úlohy spojené s kockovaným papierom sú dosť rôznorodé. Naučil som sa vypočítať plochu polygónov nakreslených na kockovanom papieri. Pri mnohých problémoch na štvorcovom papieri neexistuje všeobecné pravidlo na riešenie ani špecifické metódy a techniky. Toto je ich vlastnosť, ktorá určuje ich hodnotu pre rozvoj nie konkrétnej akademickej schopnosti alebo zručnosti, ale vo všeobecnosti schopnosti myslieť, reflektovať, analyzovať, hľadať analógie, to znamená, že tieto úlohy rozvíjajú myslenie v ich najširšom zmysle.

A tiež som sa dozvedel, že s takýmito úlohami sa počíta v skúšobných a meracích materiáloch Štátnej akadémie vied a Jednotnej štátnej skúšky. Štúdium tohto materiálu preto považujem za užitočné pre jeho uplatnenie nielen v ďalšom vzdelávacom procese, ale aj pri riešení neštandardných problémov olympiády.

2.Koncepcia oblasti

Štvorcový- číselná charakteristika dvojrozmerného geometrického útvaru, znázorňujúca veľkosť tohto útvaru. Historicky bol výpočet plochy tzv . Figúra, ktorá má plochu, sa nazýva štvorec .

Oblasť plochej postavy z hľadiska geometrie

1. Štvorcový- miera rovinného útvaru vo vzťahu k štandardnému útvaru, čo je štvorec so stranou rovnajúcou sa jednej jednotke dĺžky.

2. Štvorcový- číselná charakteristika pripisovaná plochým obrazcom určitej triedy (napríklad mnohouholníkom). Plocha štvorca so stranou rovnajúcou sa jednotkovej dĺžke, ktorá sa rovná jednotke plochy

3. Štvorcový- kladná veličina, ktorej číselná hodnota má tieto vlastnosti:

 Rovnaké čísla majú rovnaké oblasti;

 Ak je obrázok rozdelený na časti, ktoré sú jednoduchými obrázkami (t. j. tie, ktoré možno rozdeliť na konečný počet rovinných trojuholníkov), potom sa plocha tohto obrázku rovná súčtu plôch jeho častí;

 Plocha štvorca so stranou rovnajúcou sa jednej mernej jednotke sa rovná jednej.

Môžeme teda dospieť k záveru, že plocha nie je špecifická veličina, ale dáva iba určitú podmienenú charakteristiku akejkoľvek plochej postavy. Ak chcete nájsť plochu ľubovoľného obrázku, musíte určiť, koľko štvorcov so stranou rovnajúcou sa jednej jednotke dĺžky obsahuje. Vezmime si napríklad obdĺžnik, do ktorého sa presne 6-krát zmestí štvorcový centimeter. To znamená, že plocha obdĺžnika je 6 cm2.

Výber plochy štvorca so stranou rovnajúcou sa jednotke merania ako minimálnej jednotky merania všetkých plôch nie je náhodný. Je to výsledok dohody medzi ľuďmi, ktorá vznikla v priebehu „prirodzenej“ stáročnej selekcie. Okrem toho existovali ďalšie návrhy na mernú jednotku. Napríklad sa navrhlo vziať plochu rovnostranného trojuholníka ako takú jednotku (t. j. akýkoľvek plochý útvar by mohol byť reprezentovaný ako „súčet“ určitého počtu rovnostranných trojuholníkov), čo by viedlo k zmena číselného zastúpenia plôch.

Tak sa v matematike objavili vzorce na výpočet plôch a človek ich hneď nerealizoval - toto veľa vedcov žijúcich v rôznych obdobiach a rôznych krajinách. (Nesprávne vzorce nenašli miesto vo vede a zmizli do zabudnutia). Skutočné vzorce boli dopĺňané, opravované a podložené tisíce rokov, až kým sa k nám nedostali vo svojom modernom kabáte.

To isté meranie plochy spočíva v porovnaní plochy daného obrázku s plochou obrázku branou ako merná jednotka. V dôsledku porovnania sa získa určité číslo - číselná hodnota plochy daného obrázku. Toto číslo ukazuje, koľkokrát je plocha daného obrazca väčšia (alebo menšia) ako plocha obrazca braná ako jednotka plochy.

T Môžeme teda dospieť k záveru, že plocha je umelá veličina, historicky zavedená človekom na meranie nejakej vlastnosti plochého útvaru. Potreba zadania takejto hodnoty bola určená rastúcou potrebou vedieť, aké veľké je dané územie, koľko obilia je potrebné na zasiatie poľa alebo vypočítať plochu podlahy na zdobenie okrasných dlaždíc.

Pickov vzorec

Na odhadnutie plochy mnohouholníka na kockovanom papieri stačí spočítať, koľko buniek tento mnohouholník pokrýva (plochu bunky berieme ako jednu). Presnejšie, akS je plocha mnohouholníka, B je počet buniek, ktoré ležia úplne vo vnútri mnohouholníka, a G je počet buniek, ktoré majú vnútro. Budeme uvažovať len také polygóny, ktorých všetky vrcholy ležia v uzloch kockovaného papiera - tie, kde čiary polygónovej mriežky pretínajú aspoň jeden spoločný bod.

Plochu akéhokoľvek trojuholníka nakresleného na kockovanom papieri možno ľahko vypočítať tak, že ho predstavíte ako súčet alebo rozdiel plôch pravouhlých trojuholníkov a obdĺžnikov, ktorých strany sledujú čiary mriežky prechádzajúce cez vrcholy nakresleného trojuholníka.

Na výpočet plochy takéhoto mnohouholníka môžete použiť nasledujúcu vetu:

Veta . Nechaj - počet celočíselných bodov vo vnútri mnohouholníka, - počet celočíselných bodov na jeho hranici, - jeho oblasť. Potom je to spravodlivéPickov vzorec:

Príklad. Pre mnohouholník na obrázkuL = 7 (červené bodky), 9 (zelené bodky) takS = 7+ 9/2 -1 = 10,5 štvorcových jednotiek.

Pickova veta- klasický výsledok A .

Plocha trojuholníka s vrcholmi v uzloch a bez uzlov vo vnútri ani po stranách (okrem vrcholov) je 1/2. Táto skutočnosť.

3. História

Pickov vzorec objavil rakúsky matematik Georg Alexander (1859-1942) v r. . Vo veku 16 rokov Georg ukončil školu a vstúpil do školy. Vo veku 20 rokov získal právo vyučovať fyziku a matematiku. V roku 1884 Peake odišla Komu . Tam sa zoznámil s ďalším Kleinovým žiakom,. Neskôr, v roku 1885, sa vrátil do, kde strávil zvyšok svojej vedeckej kariéry.

Georg Pieck bol priateľom s Einsteinom. Peake a Einstein mali nielen spoločné vedecké záujmy, ale mali aj vášeň pre hudbu. Pick, ktorý hral v kvartete zloženom z univerzitných profesorov, uviedol Einsteina do pražských vedeckých a hudobných spoločností.

Peakov rozsah matematických záujmov bol mimoriadne široký. Predovšetkým majú viac ako 50 vedeckých prác. Pickova veta na výpočet plochy polygónu, ktorú objavil v roku 1899, sa stala všeobecne známou. V Nemecku je táto veta zahrnutá v školských učebniciach.

4.Aplikácie vzorca Pick

Pickov vzorec sa používa nielen na výpočet plôch polygónov, ale aj na riešenie mnohých problémov na úrovni olympiády.

Niekoľko príkladov použitia vzorca Pick pri riešení problémov:

1) Šachový kráľ prešiel okolo šachovnice 8 × 8 buniek a každú navštívil

pole domu presne raz a posledným ťahom sa vráti k pôvodnému

pole. Prerušovaná čiara spájajúca postupne stredy polí, ktoré

prešiel kráľom, nemá žiadne vlastné križovatky. Aká oblasť môže

obmedziť túto prerušovanú čiaru? (Strana bunky je 1.)

Z Peakovho vzorca okamžite vyplýva, že oblasť ohraničená lo-

mana, rovná 64/2 − 1 = 31; tu sú uzly mriežky stredy 64

polia a podľa podmienky všetky ležia na hranici polygónu. Takže

Aj keď existuje veľa takýchto „dráh“ kráľa, sú všetky

viazané polygóny s rovnakými plochami.

Úlohy zo skúšobných a meracích materiálov Štátnej skúšobnej agentúry a Jednotnej štátnej skúšky

Úloha B3

Nájdite oblasť obrázku zobrazenú na kockovanom papieri s veľkosťou buniek 1 cm 1 cm (pozri obrázok). Svoju odpoveď uveďte v centimetroch štvorcových.

4.Záver

Počas výskumného procesu som študovala referenčnú a populárno-náučnú literatúru. Dozvedel som sa, že problém nájsť oblasť polygónu s vrcholmi v uzloch mriežky podnietil rakúskeho matematika Piecka v roku 1899 dokázať pozoruhodný Pieckov vzorec.

Výsledkom práce som si rozšíril vedomosti o riešení úloh na kockovanom papieri, určil som si klasifikáciu skúmaných problémov a presvedčil som sa o ich rôznorodosti.

Naučil som sa vypočítať plochy mnohouholníkov nakreslených na kockovanom papieri. Uvažované úlohy majú rôznu náročnosť – od jednoduchých až po olympijské. Každý si medzi nimi môže nájsť úlohy realizovateľnej úrovne zložitosti, od ktorej bude možné prejsť k riešeniu náročnejších.

Prišiel som na to, že téma, ktorá ma zaujala, bola dosť mnohostranná, úlohy na kockovanom papieri boli pestré a pestré boli aj metódy a techniky ich riešenia. Preto sme sa rozhodli pokračovať v práci týmto smerom.

5. Použitá literatúra:

1. Vasil’ev N. B. Okolo Pickovho vzorca // Quantum. - 1974. - č.12

2. K o k e P r a s o l o v V. V. Úlohy z planimetrie. - M.: MTsNMO, 2006.t e r G.S.M. Úvod do geometrie. - M.: Veda, 1966

3.Roslova L.O., Sharygin I.F. Merania. – M.: Vydavateľstvo. "Otvorený svet", 2005.

Internetové zdroje:

:

Spätná väzba pre prácu

„Výpočet plôch rovinných útvarov. Vybrať metódu"

Zohľadnenie tejto témy zvýši kognitívnu aktivitu žiaka, ktorý následne na hodinách geometrie začne vidieť harmóniu kresby a prestane vnímať geometriu (a matematiku vôbec) ako nudnú vedu.

Posúdené učiteľom matematiky

Khodyreva Tatyana Georgievna