தேர்வு சூத்திரம்

1. அறிமுகம்

2. சிகரத்தின் சூத்திரம். கண்காட்சி ஐ.

சான்று II.

ஆதாரம் ஷ.

3. குறிக்கோள்கள்.

4. பலகோணத்தின் பகுதிக்கான சூத்திரம், செங்குத்துகளின் ஆயங்களைப் பயன்படுத்தி.

5. பணிகள்.

6. இலக்கியம்

உச்ச சூத்திரம்.

1. அறிமுகம்.

நாம் வரலாற்றிலிருந்து ஞானத்தைப் பெறுகிறோம்,

கவிதையில் - புத்தி,

கணிதத்தில் - நுண்ணறிவு.

எஃப். பேகன்

சதி ஒரு சாதாரண துண்டு காகிதத்தில் விரிவடையும்.

செல்களின் பக்கவாட்டில் இயங்கும் கோடுகள் ஒரு கட்டத்தை உருவாக்குகின்றன, மேலும் கலங்களின் மேல் பகுதிகள் இந்த கட்டத்தின் முனைகளாகும். முனைகளில் செங்குத்துகளுடன் தாளில் பலகோணத்தை வரைந்து அதன் பகுதியைக் கண்டுபிடிப்போம்.

நீங்கள் அதை வெவ்வேறு வழிகளில் தேடலாம். உதாரணமாக, நீங்கள் ஒரு பலகோணத்தை மிகவும் எளிமையான வடிவங்களாக வெட்டி, அவற்றின் பகுதிகளைக் கண்டறிந்து அவற்றைச் சேர்க்கலாம்.

ஆனால் இங்கே நிறைய சிக்கல்கள் காத்திருக்கின்றன. உருவம் எளிதில் செவ்வகங்கள், ட்ரேப்சாய்டுகள் மற்றும் முக்கோணங்களாக பிரிக்கப்பட்டுள்ளது, மேலும் அதன் பகுதி முயற்சி இல்லாமல் கணக்கிடப்படுகிறது.

பலகோணம் மிகவும் எளிமையானதாகத் தோன்றினாலும், அதன் பரப்பளவைக் கணக்கிடுவதற்கு நிறைய வேலை தேவைப்படுகிறது. பலகோணம் மிகவும் ஆடம்பரமாக இருந்தால் என்ன செய்வது? கட்டம் முனைகளில் அமைந்துள்ள பலகோணங்களின் பகுதிகளை மிகவும் எளிமையாகக் கணக்கிட முடியும் என்று மாறிவிடும்: அவற்றின் பரப்பளவை பலகோணத்தின் உள்ளேயும் எல்லையிலும் உள்ள முனைகளின் எண்ணிக்கையுடன் தொடர்புபடுத்தும் ஒரு சூத்திரம் உள்ளது. இந்த அற்புதமான மற்றும் எளிமையான சூத்திரம் பிக் ஃபார்முலா என்று அழைக்கப்படுகிறது.

2. சிகரத்தின் சூத்திரம்.

ஒரு பலகோணத்தின் செங்குத்துகள் (அவசியம் குவிந்ததாக இல்லை) ஒரு முழு எண் லட்டியின் முனைகளில் அமைந்துள்ளன. அதன் உள்ளே பி லட்டு முனைகள் உள்ளன, மற்றும் எல்லையில் ஜி முனைகள் உள்ளன. அதன் பரப்பளவு B + க்கு சமம் என்பதை நிரூபிப்போம் – 1 (சூத்திரத்தைத் தேர்ந்தெடு).

கண்காட்சி ஐ.

ஒரு பலகோணத்தை கருத்தில் கொள்வோம், அதன் செங்குத்துகள் ஒரு முழு எண் லட்டியின் முனைகளில் அமைந்துள்ளன, அதாவது அவை முழு எண் ஒருங்கிணைப்புகளைக் கொண்டுள்ளன.

நாம் பலகோணத்தை முக்கோணங்களாகப் பிரிக்கிறோம், லட்டு முனைகளில் செங்குத்துகளுடன், உள்ளே அல்லது பக்கங்களில் எந்த முனைகளும் இல்லை.

குறிப்போம்:

n- பலகோணத்தின் பக்கங்களின் எண்ணிக்கை,

மீ- உள்ளே அல்லது பக்கங்களில் முனைகளைக் கொண்டிருக்காத லட்டு முனைகளில் செங்குத்துகளைக் கொண்ட முக்கோணங்களின் எண்ணிக்கை,

பி - பலகோணத்திற்குள் உள்ள முனைகளின் எண்ணிக்கை,

Г - செங்குத்துகள் உட்பட பக்கங்களில் உள்ள முனைகளின் எண்ணிக்கை.

இந்த அனைத்து முக்கோணங்களின் பகுதிகளும் ஒரே மாதிரியாகவும் சமமாகவும் இருக்கும்.

எனவே, பலகோணத்தின் பரப்பளவு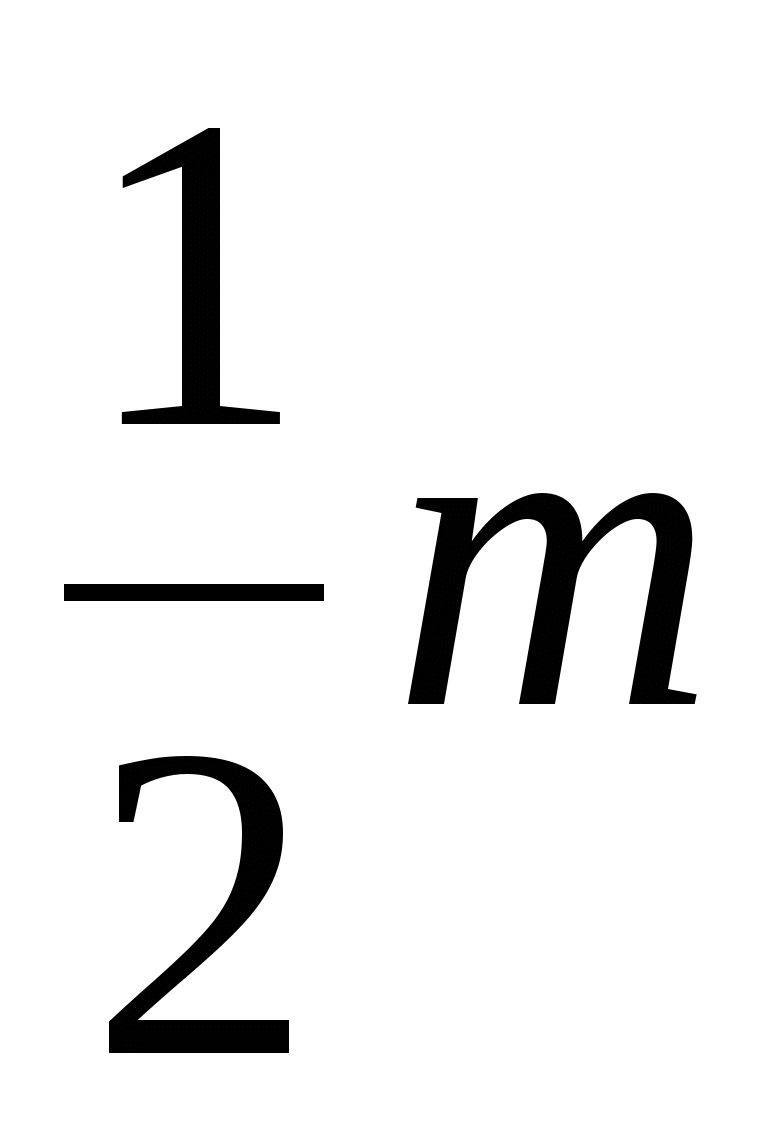
.

180 0 மீ .

இப்போது இந்த தொகையை வேறு வழியில் கண்டுபிடிப்போம்.

எந்த உள் முனையிலும் உச்சியுடன் கூடிய கோணங்களின் கூட்டுத்தொகை 360 0 ஆகும்.

பின்னர் அனைத்து உள் முனைகளிலும் உள்ள முனைகளுடன் கூடிய கோணங்களின் கூட்டுத்தொகை 360 0 V க்கு சமம்.

பக்கங்களில் உள்ள முனைகளுக்கான கோணங்களின் மொத்தத் தொகை, ஆனால் முனைகளில் இல்லை, 180 0 (G - n).

பலகோணத்தின் முனைகளில் உள்ள கோணங்களின் கூட்டுத்தொகை 180 0 ( n – 2) .

அனைத்து முக்கோணங்களின் கோணங்களின் மொத்தத் தொகை 360 0 V + 180 0 (ஜி - n) + 180 0 (n – 2).

எனவே 180 0 மீ= 360 0 V + 180 0 (ஜி - n) + 180 0 (n – 2),

180 0 மீ= 360 0 V + 180 0 G – 180 0 n + 180 0 n– 180 0 2,

180 0 மீ= 360 0 V + 180 0 G – 360 0,

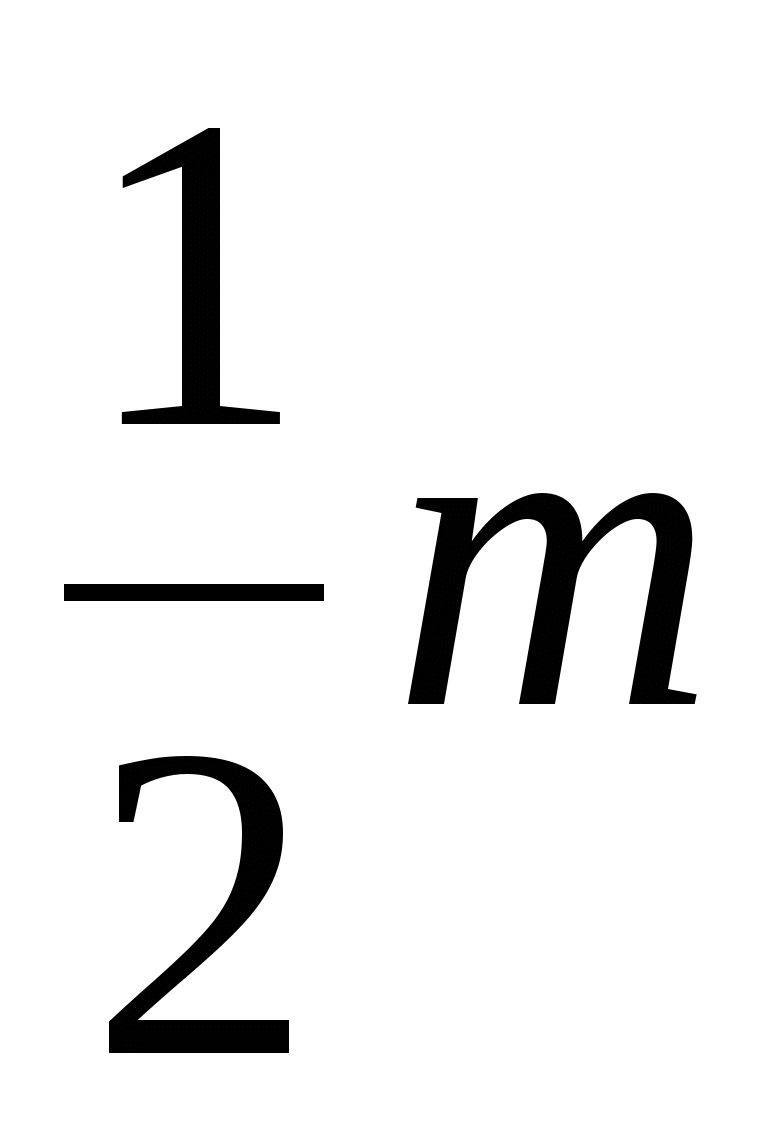= பி + – 1 ,

இதிலிருந்து பலகோணத்தின் S பகுதிக்கான வெளிப்பாட்டைப் பெறுகிறோம்:

எஸ்= பி + – 1 ,

பிக்'ஸ் ஃபார்முலா என்று அழைக்கப்படுகிறது.

படத்தில்: B = 24, D = 9, எனவே,எஸ் = 24 + – 1 = 27,5.

பீக்கின் சூத்திரத்தைப் பயன்படுத்தி முதல் பலகோணத்தின் பகுதியைக் கண்டுபிடிப்போம்:

B = 28 (பச்சை புள்ளிகள்);

G = 20 (நீல புள்ளிகள்).

நாம் பெறுகிறோம், S =
= 37 சதுர அலகுகள்

சான்று II.

ஒரு முழு எண் லட்டியின் முனைகளில் உள்ள செங்குத்துகளைக் கொண்ட ஒவ்வொரு பலகோண M க்கும் நாம் f (M) = ஒரு எண்ணை ஒதுக்குகிறோம்.
, எம் மற்றும் கோணத்திற்குச் சொந்தமான அனைத்து லேட்டிஸ் முனைகளிலும் கூட்டுத்தொகை மேற்கொள்ளப்படுகிறது பின்வருமாறு வரையறுக்கப்படுகிறது: =
பலகோணத்தின் உள் புள்ளிக்கு, =
உச்சியைத் தவிர வேறு ஒரு எல்லைப் புள்ளிக்கு, மற்றும் - உச்சி கோணம், இந்த முனை ஒரு உச்சியாக இருந்தால். f(M) = என்று பார்ப்பது எளிது
+
= பி + - 1. பலகோணத்தின் பகுதிக்கு f (M) எண் சமமாக உள்ளதா என்பதைச் சரிபார்க்க வேண்டும்.

பலகோணம் M ஐ பலகோணங்களாக M 1 மற்றும் M 2 ஆக வெட்டலாம். பின்னர் f (M) = f (M 1) + f (M 2), ஏனெனில் ஒவ்வொரு முனைக்கும் கோணங்கள் சேர்க்கப்படுகின்றன. எனவே, M, M 1 மற்றும் M 2 ஆகிய இரண்டு பலகோணங்களுக்கு பிக்கின் சூத்திரம் உண்மையாக இருந்தால், அது மூன்றாவதாகவும் இருக்கும்.

M என்றால் பக்கங்கள் கொண்ட செவ்வகம் பமற்றும் கே, பின்னல் கோடுகளுடன் இயக்கப்பட்டது

f (M) = (p – 1)(q – 1) +
= pq.

இந்த வழக்கில், பீக்கின் சூத்திரம் செல்லுபடியாகும். M 1 மற்றும் M 2 முக்கோணங்களாக மூலைவிட்டத்துடன் M ஒரு செவ்வகத்தை வெட்டுவதன் மூலம் f (M) = f (M 1) + f (M 2) மற்றும் f (M 1) = f (M 2), அது லட்டுக் கோடுகளுடன் கால்களைக் கொண்ட எந்த வலது முக்கோணத்திற்கும் பிக் சூத்திரத்தின் செல்லுபடியை நிரூபிப்பது எளிது. இந்த முக்கோணங்களில் பலவற்றை ஒரு செவ்வகத்திலிருந்து வெட்டுவதன் மூலம், நீங்கள் எந்த முக்கோணத்தையும் பெறலாம்.

பிக்கின் சூத்திரத்தின் ஆதாரத்தை நிறைவு செய்ய, எந்த பலகோணத்தையும் முக்கோணங்களாக பிரிக்கலாம்.

ஆதாரம் ஷ.

ஒரு உருவத்தின் பரப்பளவிற்கும் இந்த படத்தில் சேர்க்கப்பட்டுள்ள முனைகளின் எண்ணிக்கைக்கும் இடையிலான உறவு குறிப்பாக ஒரு செவ்வகத்தின் விஷயத்தில் தெளிவாகத் தெரியும்.

விடுங்கள் ஏபிசிடி- கட்டக் கோடுகளுடன் இயங்கும் முனைகளிலும் பக்கங்களிலும் செங்குத்துகளைக் கொண்ட ஒரு செவ்வகம்.

மூலம் குறிப்போம் INசெவ்வகத்தின் உள்ளே மற்றும் அதன் வழியாக இருக்கும் முனைகளின் எண்ணிக்கை ஜி- அதன் எல்லையில் உள்ள முனைகளின் எண்ணிக்கை. கட்டத்தை அரை கலத்தை வலதுபுறமாகவும், பாதி கலத்தை கீழேயும் நகர்த்துவோம்.

பின்னர் செவ்வகத்தின் பிரதேசத்தை முனைகளுக்கு இடையில் பின்வருமாறு "விநியோகிக்க" முடியும்: ஒவ்வொன்றும் INமுனைகள் மாற்றப்பட்ட கட்டத்தின் முழு கலத்தையும் "கட்டுப்படுத்துகின்றன", ஒவ்வொன்றும் ஜி– 4 பார்டர் அல்லாத முனைகள் அரை செல், மற்றும் ஒவ்வொரு மூலை புள்ளிகளும் கலத்தின் கால் பகுதி. எனவே, செவ்வகத்தின் பரப்பளவு S க்கு சமம்

எனவே, கட்டக் கோடுகளுடன் முனைகளிலும் பக்கங்களிலும் செங்குத்துகளைக் கொண்ட செவ்வகங்களுக்கு, நாங்கள் சூத்திரத்தை நிறுவியுள்ளோம்.

இந்த சூத்திரம் செவ்வகங்களுக்கு மட்டுமல்ல, கட்டம் முனைகளில் செங்குத்துகளைக் கொண்ட தன்னிச்சையான பலகோணங்களுக்கும் உண்மை என்பதை நிரூபிப்போம்.

மூலம் குறிப்போம் எஸ் மீ பலகோணத்தின் பகுதிஎம் முனைகளில் முனைகளுடன், மற்றும் வழியாகபி மீ - அளவு
, எங்கேIN மீ - உள்ளே உள்ள முனைகளின் எண்ணிக்கைஎம்,ஏ ஜி மீ - எல்லையில் உள்ள முனைகளின் எண்ணிக்கை. பின்னர் உச்சத்தின் சூத்திரத்தை இவ்வாறு எழுதலாம்
.

சூத்திரத்தின் ஆதாரத்தை பல படிகளாகப் பிரிப்போம்.

படி 1.

பலகோணம் என்றால்எம் 2 பலகோணங்களாக வெட்டப்பட்ட கண்ணி முனைகளில் உள்ள முனைகளுடன்எம் 1 மற்றும் எம் 2 , மேலும் கட்டம் முனைகளில் மட்டுமே செங்குத்துகளைக் கொண்டிருக்கும்
. பலகோணத்தை விடுங்கள்எம் பலகோணங்களாக வெட்டப்படுகின்றனஎம் 1 மற்றும் எம் 2 முனைகளில் முனைகளுடன் ஒரு பிரிவின் மூலம்ஏபி பிரிவில் விழுவதைத் தவிர அனைத்து முனைகளும்ஏபி, சூத்திரத்தின் இடது மற்றும் வலது பக்கங்களுக்கு சமமான பங்களிப்பைச் செய்யுங்கள். AB பிரிவில் கிடக்கும் முனைகளைக் கருத்தில் கொள்வோம்.

அத்தகைய முனை A மற்றும் B (உதாரணமாக, C) இடையே இருந்தால், பலகோணத்திற்குஎம் அது உள் மற்றும் பலகோணங்களுக்கானதுஎம் 1 மற்றும் எம் 2 - எல்லைக்கோடு. எனவே அவரது பங்களிப்புபி மீ 1 க்கு சமம், மற்றும் ஒவ்வொரு வெளிப்பாடுகளிலும்
மற்றும்
- 0.5 ஒவ்வொன்றும், அதாவது, அத்தகைய முனையின் பங்களிப்புகள்பி மீ மற்றும்
சமமாக உள்ளன.

A மற்றும் B ஆகிய முனைகளைக் கருத்தில் கொள்வோம். அவை இரண்டுக்கும் எல்லைக் கணுக்கள் எம், மற்றும் எம் 1 , எம் 2 .

எனவே, இந்த முனைகள் ஒவ்வொன்றின் பங்களிப்பும்பி மீ 0.5 a அங்குலத்திற்கு சமம்
- அலகு. இதன் பொருள் A மற்றும் B முனைகளின் மொத்த பங்களிப்புபி மீ 1 க்கு சமம், இது அவர்களின் பங்களிப்பை விட 1 குறைவு
. ஆனால்
, ஏ.

அனைத்து முனைகளின் மொத்த "பங்களிப்பிலிருந்து" பி மீ 1 கழிக்கப்படுகிறது, மற்றும் இருந்து
2 கழிக்கப்படுகிறது, மேலும் இது A மற்றும் B முனைகளின் பங்களிப்புகளில் உள்ள வேறுபாட்டை ஈடுசெய்கிறது.

எனவே,
.

படி 2.

பலகோணம் என்றால் எம்இரண்டு பலகோணங்களாக வெட்டப்பட்ட கண்ணி முனைகளில் உள்ள முனைகளுடன் எம் 1 மற்றும் எம் 2 (மேலும் முனைகளில் முனைகளுடன்) மற்றும் சில இரண்டு பலகோணங்களுக்கு சூத்திரம் சரியானது எம்.எம் 1 , எம் 2 , மூன்றாவது பலகோணத்திற்கும் இது உண்மை.

உதாரணமாக, அது உண்மையாக இருக்கட்டும்எம் 1 மற்றும் எம் 2 , அதாவது
. பின்னர் (முதல் படி மூலம்), ஆனால் (மூலம் முதல் படி) கடைசி வெளிப்பாடு சமம்பி மீ , மற்றும் சமத்துவம்
மற்றும் உச்ச சூத்திரம் உள்ளது.

படி 3.

கிரிட் முனைகளில் செங்குத்துகள் மற்றும் கட்டக் கோடுகளில் கிடக்கும் கால்கள் கொண்ட செங்கோண முக்கோணத்திற்கான உச்சத்தின் சூத்திரத்தை நிரூபிப்போம்.

முக்கோணம் ஏபிசிஅதை ஒரு செவ்வகமாக உருவாக்கவும் ஏபிசிடி .

செவ்வகங்களுக்கு, பிக்கின் சூத்திரம் சரியானது: எஸ் ஏபிசிடி = பி ஏபிசிடி . முதல் படி படி பி ஏபிசிடி = பி ஏபிசி + பி ஏசிடி , பி ஏபிசி = பி ஏசிடி , எனவே பி ஏபிசிடி = 2P ஏபிசி . ஆனால் எஸ் ஏபிசிடி = 2 எஸ் ஏபிசி . அதனால் தான் எஸ் ஏபிசி = பி ஏபிசி .

படி 4.

பிக்கின் சூத்திரம் கட்டம் முனைகளில் செங்குத்துகளைக் கொண்ட தன்னிச்சையான முக்கோணத்திற்குச் செல்லுபடியாகும்.

உருவத்தை ஆராய்ந்தால், புரிந்துகொள்வது எளிது: கட்டக் கோடுகள், பல செவ்வகங்கள் மற்றும் கட்டக் கோடுகளில் கால்களைக் கொண்ட வலது முக்கோணங்களுடன் ஒரு குறிப்பிட்ட செவ்வகத்திலிருந்து "துண்டிப்பதன் மூலம்" அத்தகைய முக்கோணத்தைப் பெறலாம். செவ்வகங்கள் மற்றும் வலது முக்கோணங்களுக்கு உச்சத்தின் சூத்திரம் உண்மையாக இருப்பதால் (படி 2 ஐ நினைவில் கொள்க) அசல் முக்கோணத்திற்கும் இது பொருந்தும்.

பலகோணத்தை கிரிட் முனைகளில் செங்குத்துகளுடன் முக்கோணங்களாக வெட்ட முடியுமானால், அதற்கு பீக்கின் சூத்திரம் சரியானது என்பதை நாங்கள் நிரூபித்துள்ளோம்.

3. குறிக்கோள்கள்.

புள்ளிவிவரங்களின் பகுதியைக் கண்டறியவும்:

1
.

பி=9

ஜி = 4

பி=9

ஜி = 5

சுய-குறுக்கீடுகள் இல்லாத பலகோணம் அதன் அனைத்து முனைகளும் முழு எண் ஒருங்கிணைப்புகளுடன் (கார்ட்டீசியன் ஒருங்கிணைப்பு அமைப்பில்) புள்ளிகளில் அமைந்திருந்தால் லட்டு என்று அழைக்கப்படுகிறது.

தேர்வு தேற்றம்

சூத்திரம்

பூஜ்ஜியம் அல்லாத பகுதியுடன் சில லட்டு பலகோணத்தை எங்களுக்கு வழங்குவோம்.

அதன் பரப்பளவைக் குறிப்போம்; பலகோணத்திற்குள் கண்டிப்பாக இருக்கும் முழு எண் ஆயத்தொலைவுகளுடன் கூடிய புள்ளிகளின் எண்ணிக்கை - மூலம் ; பலகோணத்தின் பக்கங்களில் முழு எண் ஆயத்தொலைவுகளுடன் கூடிய புள்ளிகளின் எண்ணிக்கை - மூலம் .

பின்னர் உறவினர் அழைத்தார் தேர்வு சூத்திரம்:

குறிப்பாக, I மற்றும் B இன் மதிப்புகள் ஒரு குறிப்பிட்ட பலகோணத்திற்குத் தெரிந்தால், அதன் செங்குத்துகளின் ஆயங்களை அறியாமல் கூட அதன் பரப்பளவைக் கணக்கிடலாம்.

1899 ஆம் ஆண்டில் ஆஸ்திரிய கணிதவியலாளர் ஜார்ஜ் அலெக்சாண்டர் பிக் என்பவரால் இந்த தொடர்பு கண்டுபிடிக்கப்பட்டு நிரூபிக்கப்பட்டது.

ஆதாரம்

ஆதாரம் பல நிலைகளில் மேற்கொள்ளப்படுகிறது: எளிமையான புள்ளிவிவரங்கள் முதல் தன்னிச்சையான பலகோணங்கள் வரை:

உயர் பரிமாணங்களுக்கு பொதுமைப்படுத்தல்

துரதிர்ஷ்டவசமாக, இந்த எளிய மற்றும் அழகான பீக் ஃபார்முலா உயர் பரிமாணங்களுக்கு நன்றாகப் பொதுமைப்படுத்தவில்லை.

1957 இல் டெட்ராஹெட்ரான் (தற்போது அழைக்கப்படுகிறது ரீவ் டெட்ராஹெட்ரான்) பின்வரும் முனைகளுடன்:

எந்த இயற்கை எண் எங்கே. இந்த டெட்ராஹெட்ரான், எதற்கும், முழு எண் ஒருங்கிணைப்புகளுடன் ஒரு புள்ளியைக் கொண்டிருக்கவில்லை, அதன் எல்லையில் நான்கு புள்ளிகள் மட்டுமே உள்ளன , , , மற்றவை இல்லை. எனவே, இந்த டெட்ராஹெட்ரானின் அளவு மற்றும் பரப்பளவு வேறுபட்டிருக்கலாம், அதே நேரத்தில் உள்ளேயும் எல்லையிலும் உள்ள புள்ளிகளின் எண்ணிக்கை மாறாமல் இருக்கும்; எனவே, பிக்கின் சூத்திரம் முப்பரிமாண வழக்கில் கூட பொதுமைப்படுத்தலை அனுமதிக்காது.

ஆயினும்கூட, உயர் பரிமாணங்களின் இடைவெளிகளுக்கு இன்னும் சில ஒத்த பொதுமைப்படுத்தல் உள்ளது - இது எர்ஹார்ட் பல்லுறுப்புக்கோவைகள்(Ehrhart Polynomial), ஆனால் அவை மிகவும் சிக்கலானவை, மேலும் உருவத்தின் உள்ளேயும் எல்லையிலும் உள்ள புள்ளிகளின் எண்ணிக்கையை மட்டும் சார்ந்தது அல்ல.

சரிபார்க்கப்பட்ட காகிதத்தில் பலகோணத்தின் பரப்பளவை மதிப்பிடுவதற்கு, இந்த பலகோணம் எத்தனை செல்களை உள்ளடக்கியது என்பதைக் கணக்கிடுவது போதுமானது (ஒரு கலத்தின் பகுதியை நாம் ஒன்றாக எடுத்துக்கொள்கிறோம்). இன்னும் துல்லியமாக, என்றால் எஸ்- பலகோணத்தின் பரப்பளவு, - பலகோணத்திற்குள் முழுவதுமாக இருக்கும் கலங்களின் எண்ணிக்கை, மற்றும் - பலகோணத்தின் உட்புறத்துடன் குறைந்தபட்சம் ஒரு பொதுவான புள்ளியைக் கொண்டிருக்கும் கலங்களின் எண்ணிக்கை.

கீழே நாம் அத்தகைய பலகோணங்களை மட்டுமே கருத்தில் கொள்வோம், அவற்றின் செங்குத்துகள் அனைத்தும் சரிபார்க்கப்பட்ட காகிதத்தின் முனைகளில் உள்ளன - கட்டக் கோடுகள் வெட்டும் இடங்களில். அத்தகைய பலகோணங்களுக்கு பின்வரும் சூத்திரத்தை ஒருவர் குறிப்பிடலாம்:

பகுதி எங்கே, ஆர்- பலகோணத்திற்குள் கண்டிப்பாக இருக்கும் முனைகளின் எண்ணிக்கை.

இந்த சூத்திரத்தை 1899 இல் கண்டுபிடித்த கணிதவியலாளரின் பெயரால் "பிக் ஃபார்முலா" என்று அழைக்கப்படுகிறது.

எளிய முக்கோணங்கள்

சரிபார்க்கப்பட்ட காகிதத்தில் வரையப்பட்ட எந்த முக்கோணத்தின் பரப்பளவும், வரையப்பட்ட முக்கோணத்தின் செங்குத்துகள் வழியாக செல்லும் கட்டக் கோடுகளைப் பின்தொடர்ந்து செல்லும் வலது முக்கோணங்கள் மற்றும் செவ்வகங்களின் பகுதிகளின் கூட்டுத்தொகை அல்லது வேறுபாட்டின் மூலம் எளிதாகக் கணக்கிட முடியும். இதைச் செய்தபின், எடுத்துக்காட்டாக, படம் 1.34 இல் காட்டப்பட்டுள்ள முக்கோணங்களுக்கு, பகுதி எப்போதும் “பெறப்பட்ட” எண்ணுக்கு சமமாக இருப்பதை உறுதிசெய்யலாம் - படிவத்தின் எண், அங்கு ஒரு முழு எண்.

முக்கோணத்தின் முனைகளைத் தவிர்த்து, அதன் உள்ளே அல்லது அதன் பக்கங்களில் கண்ணி முனைகள் இல்லை என்றால் அதை எளிமையானது என்று அழைப்போம். படத்தில் உள்ள அனைத்து எளிய முக்கோணங்களும். 1.34 பரப்பளவு கொண்டது. இது தற்செயலானதல்ல என்று பார்ப்போம்.

பணி. ஆரம்ப நேரத்தில் மூன்று வெட்டுக்கிளிகள் (மூன்று புள்ளிகள்) ஒரு கலத்தின் மூன்று முனைகளில் அமர்ந்து, பின்னர் "பாய்ச்சல் விளையாட" தொடங்கும்: ஒவ்வொன்றும் மற்ற இரண்டில் ஒன்றைத் தாண்டிச் செல்லலாம், அதன் பிறகு அது ஒரு புள்ளி சமச்சீர் உறவில் முடிவடைகிறது. அதன் சொந்த (படம். 1.35, தெளிவாக, அத்தகைய தாவல்கள் எந்த எண் பிறகு வெட்டுக்கிளிகள் சரிபார்க்கப்பட்ட காகித முடிச்சுகள் விழும் என்று). வெட்டுக்கிளிகள் சில தாவல்களுக்குப் பிறகு எந்த மூன்று மடங்கு புள்ளிகளில் முடிவடையும்?

மூன்று வெட்டுக்கிளிகள் ஒரே நேரத்தில் அதன் முனைகளில் தோன்றினால், முக்கோணத்தை அடையக்கூடியது என்று அழைப்போம், அவை ஆரம்பத்தில் ஒரு கலத்தின் மூன்று முனைகளில் இருந்தன; ஒரு ஜம்ப்பை ஒரு முக்கோணத்தின் மாற்றம் என்று அழைப்போம், இதில் ஒரு முனையானது மற்ற இரண்டு செங்குத்துகளில் ஏதேனும் ஒன்றைப் பொறுத்து சமச்சீரான ஒரு புள்ளிக்கு செல்கிறது (இந்த இரண்டு செங்குத்துகளும் இடத்தில் இருக்கும்).

தேற்றம் 1. சரிபார்க்கப்பட்ட காகித முனைகளில் செங்குத்துகளைக் கொண்ட முக்கோணங்களின் பின்வரும் மூன்று பண்புகள் ஒன்றுக்கொன்று சமமானவை:

1) முக்கோணத்தில் பரப்பளவு உள்ளது,

2) முக்கோணம் எளிமையானது,

3) முக்கோணம் அடையக்கூடியது.

ஒரு எளிய முக்கோணத்தின் பின்வரும் பண்புகளைப் பற்றி அறிந்து கொள்வோம், இது இந்த தேற்றத்தின் செல்லுபடியாகும்.

1. குதிக்கும் போது முக்கோணத்தின் பரப்பளவு மாறாது.

2. அடையக்கூடிய எந்த முக்கோணமும் பரப்பளவைக் கொண்டுள்ளது.

3. நீங்கள் ஒரு எளிய முக்கோணத்தை நிறைவு செய்தால் ஏபிசிஇணையான வரைபடத்திற்கு ஏபிசிடி, பின்னர் இந்த இணையான வரைபடத்தின் உள்ளே அல்லது பக்கங்களில் முனைகள் இருக்காது (செங்குத்துகளை எண்ணுவதில்லை).

4. குதிக்கும் போது ஒரு எளிய முக்கோணத்திலிருந்து, ஒரு எளிய முக்கோணம் பெறப்படுகிறது.

5. ஒரு எளிய முக்கோணத்திலிருந்து, கோணங்களில் ஒன்று மழுங்கிய அல்லது நேராக இருக்கும் (மேலும் பிந்தைய வழக்கு ஒரு கலத்திற்கு மூன்று செங்குத்துகள் இருக்கும் ஒரு முக்கோணத்திற்கு மட்டுமே சாத்தியமாகும்; 1, 1 பக்கங்களைக் கொண்ட அத்தகைய எளிய முக்கோணம் குறைந்தபட்சம் என்று அழைக்கப்படும்.)

6. எந்தவொரு எளிய அல்லாத குறைந்தபட்ச முக்கோணத்திலிருந்தும் நீங்கள் ஒரு முக்கோணத்தை ஒரே தாவலில் பெறலாம், அதன் நீளமான பக்கமானது அசல் ஒன்றின் நீளமான பக்கத்தை விட சிறியதாக இருக்கும்.

7. எந்தவொரு எளிய முக்கோணத்தையும் ஒரு குறிப்பிட்ட எண்ணிக்கையிலான தாவல்கள் மூலம் குறைந்தபட்ச ஒன்றாக மாற்றலாம்.

8. எந்த எளிய முக்கோணமும் அடையக்கூடியது.

9. எந்த எளிய முக்கோணமும் பரப்பளவைக் கொண்டுள்ளது.

10. எந்த முக்கோணத்தையும் எளிமையானதாக வெட்டலாம்.

11. எந்த முக்கோணத்தின் பரப்பளவும் சமமாக இருக்கும், எந்த நேரத்திலும் அது பகா எண்களாக வெட்டப்பட்டால், அவற்றின் எண்ணிக்கை சமமாக இருக்கும் மீ.

12. பகுதியின் எந்த முக்கோணமும் எளிமையானது.

13. ஏதேனும் இரண்டு முனைகளுக்கு ஏமற்றும் INலட்டுகள், வேறு முனைகள் இல்லாத ஒரு பிரிவில், ஒரு முனை உள்ளது உடன்அத்தகைய ஒரு முக்கோணம் ஏபிசி- எளிய.

14. முடிச்சு உடன்முந்தைய சொத்தில் நீங்கள் எப்போதும் கோணத்தை தேர்வு செய்யலாம் DIAமழுங்கிய அல்லது நேராக இருக்கும்.

15. சரிபார்க்கப்பட்ட விமானம் சம இணையான வரைபடங்களாக வெட்டப்பட வேண்டும், இதனால் அனைத்து முனைகளும் இணையான வரைபடங்களின் செங்குத்துகளாக இருக்கும். இந்த இணையான வரைபடங்களில் ஒன்றை அதன் மூலைவிட்டத்தால் வெட்டப்பட்ட ஒவ்வொரு முக்கோணமும் எளிமையானது.

16. (தலைகீழ் 15). முக்கோணம் ஏபிசி- சாத்தியமான அனைத்து முக்கோணங்களும் பெறப்பட்டால் மட்டுமே எளிமையானது ஏபிசிமுனையை மாற்றும் இணை மொழிபெயர்ப்பு ஏவெவ்வேறு லட்டு முனைகளில், ஒன்றையொன்று ஒன்றுடன் ஒன்று சேர்க்க வேண்டாம்.

17. லேட்டிஸ் - சரிபார்க்கப்பட்ட தாளின் முனைகள் - செல்கள் (படம் 1.36) கொண்ட நான்கு சப்லேட்டிஸாகப் பிரிக்கப்பட்டிருந்தால், ஒரு எளிய முக்கோணத்தின் செங்குத்துகள் அவசியமாக மூன்று வெவ்வேறு சப்லேட்டிஸாக விழும் (மூன்றும் வெவ்வேறு பெயர்களைக் கொண்டுள்ளன).

பின்வரும் இரண்டு பண்புகள் மூன்று வெட்டுக்கிளிகள் பிரச்சனைக்கு விடை அளிக்கின்றன.

18. மூன்று வெட்டுக்கிளிகள் ஒரே நேரத்தில், ஒரு எளிய முக்கோணத்தின் முனைகளாக செயல்படும் மற்றும் ஆரம்ப முக்கோணத்தின் தொடர்புடைய செங்குத்துகளின் அதே அடையாளத்தைக் கொண்டிருக்கும் அந்த மூன்று மடங்கு புள்ளிகளை மட்டுமே தாக்க முடியும்.

19. இரண்டு வெட்டுக்கிளிகள் ஒரே நேரத்தில் மற்ற கணுக்கள் இல்லாத பிரிவில் தொடர்புடைய குறிகளின் அந்த ஜோடி கணுக்களை மட்டுமே தாக்க முடியும்.

பலகோண முக்கோணம்

தேர்வு சூத்திரத்தில் உள்ள மதிப்புகளுக்கு ஒத்திருக்கும் ஒரு குறிப்பிட்ட வகை பலகோணங்களை சரிபார்க்கப்பட்ட காகிதத்தில் பரிசீலிப்போம். ஆனால் இந்த குறிப்பிட்ட வழக்கில் இருந்து நீங்கள் ஒரு தன்னிச்சையான பலகோணத்தை முக்கோணங்களாக வெட்டுவதற்கான தேற்றத்தைப் பயன்படுத்தி, மிகவும் பொதுவான ஒன்றிற்கு நேராக செல்லலாம் (சரிபார்க்கப்பட்ட காகிதம் இனி தேவையில்லை).

சில பலகோணங்களும் சில வரையறுக்கப்பட்ட தொகுப்புகளும் விமானத்தில் கொடுக்கப்பட வேண்டும் TOபலகோணத்தின் உள்ளேயும் அதன் எல்லையிலும் உள்ள புள்ளிகள் (மற்றும் பலகோணத்தின் அனைத்து முனைகளும் தொகுப்பைச் சேர்ந்தவை TO).

முனைகளுடன் கூடிய முக்கோணம் TOகொடுக்கப்பட்ட பலகோணத்தை தொகுப்பில் உள்ள செங்குத்துகளுடன் முக்கோணங்களாகப் பிரிப்பது என்று அழைக்கப்படுகிறது TOஒவ்வொரு புள்ளியிலிருந்தும் TOஇந்த புள்ளியை சேர்ந்த அந்த முக்கோண முக்கோணங்கள் ஒவ்வொன்றின் உச்சியாக செயல்படுகிறது (அதாவது, புள்ளிகள் TOமுக்கோணங்களின் உள்ளே அல்லது பக்கங்களில் விழ வேண்டாம், அத்தி. 1.37).

தேற்றம் 2. அ) ஏதேனும் nஒரு முக்கோணத்தை குறுக்காக முக்கோணங்களாக வெட்டலாம், மேலும் முக்கோணங்களின் எண்ணிக்கை சமமாக இருக்கும் n- 2 (இந்தப் பகிர்வு என்பது செங்குத்துகளில் செங்குத்துகளைக் கொண்ட ஒரு முக்கோணமாகும் n-கோன்).

b) பலகோணத்தின் எல்லை குறிக்கப்படட்டும் ஆர்புள்ளிகள் (அனைத்து செங்குத்துகள் உட்பட), உள்ளே - மேலும் iபுள்ளிகள். பின்னர் குறிக்கப்பட்ட புள்ளிகளில் செங்குத்துகளுடன் ஒரு முக்கோணம் உள்ளது, அத்தகைய முக்கோணத்தின் முக்கோணங்களின் எண்ணிக்கை சமமாக இருக்கும்.

நிச்சயமாக, a) என்பது b இன் சிறப்பு வழக்கு), எப்போது.

இந்த தேற்றத்தின் செல்லுபடியாகும் தன்மை பின்வரும் அறிக்கைகளிலிருந்து பின்பற்றப்படுகிறது.

1) மிகப்பெரிய கோணத்தின் உச்சியில் இருந்து n-gon () பலகோணத்திற்குள் முழுவதுமாக இருக்கும் ஒரு மூலைவிட்டத்தை வரைய எப்போதும் சாத்தியம்.

2) என்றால் n- சதுரம் குறுக்காக வெட்டப்பட்டது ஆர்-சதுரம் மற்றும் கே-கோன், பின்னர்.

3) கோணங்களின் கூட்டுத்தொகை n-கோன் சமம்.

4) ஏதேனும் n-ஒரு முக்கோணத்தை முக்கோணங்களாக குறுக்காக வெட்டலாம்.

5) எந்த முக்கோணத்திற்கும், அதன் உள்ளேயும் எல்லையிலும் பல புள்ளிகள் குறிக்கப்பட்டிருக்கும் (அதன் மூன்று முனைகளும் உட்பட), குறிக்கப்பட்ட புள்ளிகளில் செங்குத்துகளுடன் ஒரு முக்கோணம் உள்ளது.

6) எவருக்கும் இதே நிலைதான் n-கோன்.

7) முக்கோண முக்கோணங்களின் எண்ணிக்கை சமம், எங்கே iமற்றும் ஆர்- பலகோணத்தின் உள்ளேயும் எல்லையிலும் முறையே குறிக்கப்பட்ட பல புள்ளிகளின் எண்ணிக்கை. பிரிவினையை அழைப்போம் nபகிர்வின் பலகோணங்களில் ஒன்றின் ஒவ்வொரு உச்சியும் அது சேர்ந்த பகிர்வின் மற்ற அனைத்து பலகோணங்களின் உச்சியாக செயல்பட்டால் பல பலகோணங்களுக்குள் சென்றது சரியானது. 8) உச்சிகளில் இருந்து இருந்தால் கே-கோன்கள் சரியான முறையில் பிரிக்கப்பட்டுள்ளன n-கோன், iசெங்குத்துகள் உள்ளே மற்றும் ஆர்- எல்லையில் n-gon, பின்னர் அளவு கே-கோன்கள் சமம்

9) இந்த புள்ளிகளில் முனைகள் கொண்ட விமானம் மற்றும் பிரிவுகளின் புள்ளிகள் பலகோணத்தை உருவாக்கினால், சரியாக பலகோணங்களாக பிரிக்கப்பட்டால், பின்னர் (படம் 1.38)

கோட்பாடுகள் 1 மற்றும் 2 இலிருந்து உச்ச சூத்திரம் பின்வருமாறு:

1.5 ஒரு செங்கோண முக்கோணத்தின் பக்கங்களில் கட்டப்பட்ட சதுரங்களின் பகுதிகளின் கூட்டுத்தொகையில் பித்தகோரியன் தேற்றம்

தேற்றம். ஒரு செங்கோண முக்கோணத்தின் பக்கங்களில் கட்டப்பட்ட சதுரங்களின் பகுதிகளின் கூட்டுத்தொகை இந்த முக்கோணத்தின் ஹைப்போடென்யூஸில் கட்டப்பட்ட சதுரத்தின் பரப்பளவிற்கு சமம். விடுங்கள் ஏபிசி(படம் 1.39) ஒரு செங்கோண முக்கோணம், மற்றும் BDEA, AFGEமற்றும் BCKH- அதன் கால்கள் மற்றும் ஹைப்போடென்யூஸில் கட்டப்பட்ட சதுரங்கள்; முதல் இரண்டு சதுரங்களின் பகுதிகளின் கூட்டுத்தொகை மூன்றாவது சதுரத்தின் பரப்பளவிற்கு சமம் என்பதை நீங்கள் நிரூபிக்க வேண்டும்.

நிறைவேற்றுவோம் சூரியன். பின்னர் சதுரம் BCKHஇரண்டு செவ்வகங்களாக பிரிக்கப்படும். செவ்வகம் என்பதை நிரூபிப்போம் BLMHஒரு சதுரத்திற்கு சமம் BDEA, மற்றும் செவ்வகம் LCKMஒரு சதுரத்திற்கு சமம் AFGC.

துணை வரிகளை வரைவோம் DCமற்றும் AN. முக்கோணங்களைக் கவனியுங்கள் டிசிபிமற்றும் ஏபிஎச். முக்கோணம் டிசிபிஒரு அடிப்படை கொண்டது BD, சதுரத்துடன் பொதுவானது BDEA, மற்றும் உயரம் சிஎன், உயரத்திற்கு சமம் ஏபிஇந்த சதுரத்தின் அரை சதுரத்திற்கு சமம். முக்கோணம் ஏவிஎன்ஒரு அடிப்படை கொண்டது வி.என், செவ்வகத்துடன் பொதுவானது BLMH, மற்றும் உயரம் AR, உயரத்திற்கு சமம் பி.எல்.இந்த செவ்வகத்தின் அளவு, அதன் பாதிக்கு சமம். இந்த இரண்டு முக்கோணங்களையும் ஒன்றோடொன்று ஒப்பிட்டுப் பார்த்தால், அவை இருப்பதைக் காண்கிறோம் BD = VAமற்றும் BC = VN(சதுரத்தின் பக்கங்களைப் போல);

மேலும், DCB = ஏவிஎன், இந்தக் கோணங்கள் ஒவ்வொன்றும் ஒரு பொதுவான பகுதியைக் கொண்டிருப்பதால் - ஏபிசிமற்றும் வலது கோணம். எனவே முக்கோணங்கள் ஏவிஎன்மற்றும் BCDசமமாக உள்ளன. அது செவ்வகம் என்று பின்வருமாறு பிஎல்எம்என்ஒரு சதுரத்திற்கு சமம் BDEA. அதே வழியில் அது செவ்வகம் என்று நிரூபிக்கப்பட்டுள்ளது எல்.ஜி.கே.எம்ஒரு சதுரத்திற்கு சமம் AFGC. அது சதுரம் என்று பின்வருமாறு வி.எஸ்.கே.என்சதுரங்களின் கூட்டுத்தொகைக்கு சமம் BDEAமற்றும் AFGC.

ஒரு உருவத்தின் பரப்பளவைக் கணக்கிடுதல்.

தேர்வு முறை

இர்குட்ஸ்கில் உள்ள MBOU மேல்நிலைப் பள்ளி எண் 23 இல் 5B வகுப்பு மாணவரின் வேலை

பால்சுகோவா அலெக்ஸாண்ட்ரா

தலைவர்: கோடிரேவா டி.ஜி.

2014

ஒரு உருவத்தின் பரப்பளவைக் கணக்கிடுதல். தேர்வு முறை

ஆய்வு பொருள் : சரிபார்க்கப்பட்ட காகிதத்தில் உள்ள சிக்கல்கள்

ஆய்வுப் பொருள் : பலகோணத்தின் பரப்பளவை சரிபார்க்கப்பட்ட காகிதத்தில் கணக்கிடுவதில் உள்ள சிக்கல்கள், அவற்றைத் தீர்ப்பதற்கான முறைகள் மற்றும் நுட்பங்கள்.

ஆராய்ச்சி முறைகள் : ஒப்பீடு, பொதுமைப்படுத்தல், ஒப்புமைகள், இலக்கியம் மற்றும் இணைய வளங்களின் ஆய்வு, தகவல் பகுப்பாய்வு.

ஆய்வின் நோக்கம்:

முக்கிய, சுவாரஸ்யமான, புரிந்துகொள்ளக்கூடிய தகவலைத் தேர்ந்தெடுக்கவும்

பெறப்பட்ட தகவல்களை பகுப்பாய்வு செய்து முறைப்படுத்தவும்

சரிபார்க்கப்பட்ட காகிதத்தில் சிக்கல்களைத் தீர்ப்பதற்கான பல்வேறு முறைகள் மற்றும் நுட்பங்களைக் கண்டறியவும்

பிக் சூத்திரத்தைப் பயன்படுத்தி வடிவியல் உருவங்களின் பகுதிகளைக் கணக்கிடுவதற்கான சூத்திரங்களைச் சரிபார்க்கவும்

சேகரிக்கப்பட்ட பொருளை வழங்க, வேலையின் மின்னணு விளக்கக்காட்சியை உருவாக்கவும்

வடிவியல் என்பது நமது மனத் திறன்களைக் கூர்மைப்படுத்துவதற்கும், சரியாக சிந்திக்கவும் நியாயப்படுத்தவும் உதவும் மிக சக்திவாய்ந்த வழிமுறையாகும்.

(ஜி. கலிலியோ)

தலைப்பின் பொருத்தம்

கணிதத்தின் மீதான ஆர்வம் பெரும்பாலும் ஒரு சிக்கலைப் பற்றி சிந்திக்கத் தொடங்குகிறது. எனவே, "பலகோணங்களின் பகுதி" என்ற தலைப்பைப் படிக்கும்போது, ​​​​பாடப்புத்தகத்தில் விவாதிக்கப்பட்ட சிக்கல்களிலிருந்து வேறுபட்ட சிக்கல்கள் உள்ளதா என்ற கேள்வி எழுகிறது. இத்தகைய சிக்கல்களில் சரிபார்க்கப்பட்ட காகிதத்தில் உள்ள சிக்கல்களும் அடங்கும். இத்தகைய சிக்கல்களின் தனித்தன்மை என்ன, சரிபார்க்கப்பட்ட காகிதத்தில் சிக்கல்களைத் தீர்ப்பதற்கான சிறப்பு முறைகள் மற்றும் நுட்பங்கள் உள்ளன. ஒரு கணித பாடத்தின் போது, ​​​​ஆசிரியர் பலகோணங்களைக் கணக்கிடுவதற்கான ஒரு சுவாரஸ்யமான முறையை எங்களுக்கு அறிமுகப்படுத்தினார். நான் இந்த தலைப்பில் இலக்கியம் மற்றும் இணைய வளங்களைப் படிக்க ஆரம்பித்தேன். ஒரு சரிபார்க்கப்பட்ட விமானத்தில், அதாவது முடிவில்லாத காகிதத்தில், ஒரே மாதிரியான சதுரங்களில் வரிசையாகக் கவர்ச்சிகரமான ஒன்றைக் காணலாம் என்று தோன்றுகிறது. சரிபார்க்கப்பட்ட காகிதத்துடன் தொடர்புடைய பணிகள் மிகவும் வேறுபட்டவை என்று மாறிவிடும். சரிபார்க்கப்பட்ட காகிதத்தில் வரையப்பட்ட பலகோணங்களின் பரப்பளவை எவ்வாறு கணக்கிடுவது என்பதை நான் கற்றுக்கொண்டேன். ஸ்கொயர் பேப்பரில் உள்ள பல பிரச்சனைகளுக்கு தீர்வுக்கான பொதுவான விதி அல்லது குறிப்பிட்ட முறைகள் மற்றும் நுட்பங்கள் இல்லை. இது அவர்களின் சொத்து, இது ஒரு குறிப்பிட்ட கல்வித் திறன் அல்லது திறமையின் வளர்ச்சிக்கான மதிப்பை தீர்மானிக்கிறது, ஆனால் பொதுவாக சிந்திக்க, பிரதிபலிக்க, பகுப்பாய்வு, ஒப்புமைகளைத் தேடும் திறன், அதாவது, இந்த பணிகள் அவற்றின் பரந்த அர்த்தத்தில் சிந்தனை திறன்களை வளர்க்கின்றன.

மாநில அறிவியல் அகாடமி மற்றும் ஒருங்கிணைந்த மாநிலத் தேர்வின் சோதனை மற்றும் அளவீட்டுப் பொருட்களில் இத்தகைய பணிகள் கருதப்படுகின்றன என்பதையும் நான் அறிந்தேன். எனவே, இந்த பொருளைப் படிப்பது மேலதிக கல்விச் செயல்பாட்டில் மட்டுமல்லாமல், தரமற்ற ஒலிம்பியாட் சிக்கல்களைத் தீர்ப்பதற்கும் பயனுள்ளதாக இருக்கும் என்று நான் கருதுகிறேன்.

2.பகுதியின் கருத்து

சதுரம்- இந்த உருவத்தின் அளவைக் காட்டும் இரு பரிமாண வடிவியல் உருவத்தின் எண்ணியல் பண்பு. வரலாற்று ரீதியாக, பகுதி கணக்கீடு அழைக்கப்படுகிறது . பரப்பளவைக் கொண்ட ஒரு உருவம் அழைக்கப்படுகிறது சதுரமானது .

வடிவவியலின் அடிப்படையில் ஒரு தட்டையான உருவத்தின் பரப்பளவு

1. சதுரம்ஒரு நிலையான உருவத்துடன் தொடர்புடைய ஒரு விமான உருவத்தின் அளவீடு, இது ஒரு அலகு நீளத்திற்கு சமமான பக்கத்துடன் ஒரு சதுரம்.

2. சதுரம்- ஒரு குறிப்பிட்ட வகுப்பின் தட்டையான உருவங்களுக்குக் காரணமான ஒரு எண் பண்பு (உதாரணமாக, பலகோணங்கள்). நீளத்தின் அலகுக்கு சமமான பக்கத்துடன் ஒரு சதுரத்தின் பரப்பளவு, பகுதியின் அலகுக்கு சமமாக எடுத்துக் கொள்ளப்படுகிறது

3. சதுரம்- நேர்மறை அளவு, அதன் எண் மதிப்பு பின்வரும் பண்புகளைக் கொண்டுள்ளது:

 சம புள்ளிவிவரங்கள் சம பகுதிகளைக் கொண்டுள்ளன;

 ஒரு உருவம் எளிய உருவங்களாகப் பிரிக்கப்பட்டால் (அதாவது, வரையறுக்கப்பட்ட எண்ணிக்கையிலான விமான முக்கோணங்களாகப் பிரிக்கக்கூடியவை), இந்த உருவத்தின் பரப்பளவு அதன் பகுதிகளின் பகுதிகளின் கூட்டுத்தொகைக்கு சமம்;

 ஒரு பக்க அளவீட்டு அலகுக்கு சமமான ஒரு சதுரத்தின் பரப்பளவு ஒன்றுக்கு சமம்.

எனவே, பகுதி ஒரு குறிப்பிட்ட அளவு அல்ல, ஆனால் எந்த தட்டையான உருவத்திற்கும் சில நிபந்தனை பண்புகளை மட்டுமே அளிக்கிறது என்று நாம் முடிவு செய்யலாம். ஒரு தன்னிச்சையான உருவத்தின் பரப்பளவைக் கண்டுபிடிக்க, ஒரு அலகு நீளத்திற்கு சமமான பக்கத்துடன் எத்தனை சதுரங்கள் உள்ளன என்பதை நீங்கள் தீர்மானிக்க வேண்டும். உதாரணமாக, ஒரு செவ்வகத்தை எடுத்துக் கொள்ளுங்கள், அதில் ஒரு சதுர சென்டிமீட்டர் சரியாக 6 முறை பொருந்தும். இதன் பொருள் செவ்வகத்தின் பரப்பளவு 6 செமீ 2 ஆகும்.

அனைத்து பகுதிகளின் குறைந்தபட்ச அளவீட்டு அலகு அளவீட்டு அலகுக்கு சமமான பக்கத்துடன் ஒரு சதுரத்தின் பகுதியைத் தேர்ந்தெடுப்பது தற்செயலானது அல்ல. இது "இயற்கை" பல நூற்றாண்டுகள் பழமையான தேர்வின் போக்கில் எழுந்த மக்களிடையே ஒரு ஒப்பந்தத்தின் விளைவாகும். கூடுதலாக, அளவீட்டு அலகுக்கான பிற முன்மொழிவுகள் இருந்தன. எனவே, எடுத்துக்காட்டாக, ஒரு சமபக்க முக்கோணத்தின் பரப்பளவை அத்தகைய அலகாக எடுத்துக் கொள்ள முன்மொழியப்பட்டது (அதாவது, எந்த தட்டையான உருவமும் ஒரு குறிப்பிட்ட எண்ணிக்கையிலான சமபக்க முக்கோணங்களின் "தொகை" என குறிப்பிடப்படலாம்), இது ஒரு பகுதிகளின் எண் பிரதிநிதித்துவத்தில் மாற்றம்.

இவ்வாறு, பகுதிகளைக் கணக்கிடுவதற்கான சூத்திரங்கள் கணிதத்தில் தோன்றின, அவை மனிதனால் உடனடியாக உணரப்படவில்லை - இது பல விஞ்ஞானிகள் வெவ்வேறு காலங்களில் மற்றும் வெவ்வேறு நாடுகளில் வாழ்கின்றனர். (தவறான சூத்திரங்கள் அறிவியலில் இடம் பெறவில்லை மற்றும் மறதியில் மறைந்துவிட்டன). உண்மையான சூத்திரங்கள் அவற்றின் நவீன தோற்றத்தில் நம்மை அடையும் வரை ஆயிரக்கணக்கான ஆண்டுகளாக கூடுதலாக, திருத்தப்பட்டு, நிரூபிக்கப்பட்டன.

அதே விஷயம் பகுதி அளவீடுகொடுக்கப்பட்ட உருவத்தின் பரப்பளவை அளவீட்டு அலகாக எடுக்கப்பட்ட உருவத்தின் பரப்பளவுடன் ஒப்பிடுவதைக் கொண்டுள்ளது. ஒப்பிடுவதன் விளைவாக, ஒரு குறிப்பிட்ட எண் பெறப்படுகிறது - கொடுக்கப்பட்ட உருவத்தின் பகுதியின் எண் மதிப்பு. இந்த எண், கொடுக்கப்பட்ட உருவத்தின் பரப்பளவு, பரப்பளவு அளவீட்டு அலகு என எடுக்கப்பட்ட உருவத்தின் பரப்பளவை விட எத்தனை மடங்கு அதிகமாக (அல்லது குறைவாக) உள்ளது என்பதைக் காட்டுகிறது.

டி எனவே, பகுதி ஒரு செயற்கை அளவு என்று நாம் முடிவு செய்யலாம், வரலாற்று ரீதியாக ஒரு தட்டையான உருவத்தின் சில சொத்துக்களை அளவிட மனிதனால் அறிமுகப்படுத்தப்பட்டது. அத்தகைய மதிப்பை உள்ளிட வேண்டிய அவசியம், கொடுக்கப்பட்ட பிரதேசம் எவ்வளவு பெரியது, ஒரு வயலை விதைக்க எவ்வளவு தானியங்கள் தேவை அல்லது அலங்கார ஓடுகளை அலங்கரிப்பதற்கான தரையின் மேற்பரப்பைக் கணக்கிடுவதற்கான வளர்ந்து வரும் தேவையால் தீர்மானிக்கப்பட்டது.

தேர்வு சூத்திரம்

சரிபார்க்கப்பட்ட காகிதத்தில் பலகோணத்தின் பரப்பளவை மதிப்பிடுவதற்கு, இந்த பலகோணம் எத்தனை செல்களை உள்ளடக்கியது என்பதைக் கணக்கிடுவது போதுமானது (ஒரு கலத்தின் பகுதியை நாம் ஒன்றாக எடுத்துக்கொள்கிறோம்). இன்னும் துல்லியமாக, என்றால்எஸ் பலகோணத்தின் பரப்பளவு, B என்பது பலகோணத்திற்குள் முழுவதுமாக இருக்கும் கலங்களின் எண்ணிக்கை, மற்றும் G என்பது உட்புறம் கொண்ட கலங்களின் எண்ணிக்கை. அத்தகைய பலகோணங்களை மட்டுமே நாங்கள் கருத்தில் கொள்வோம், அவற்றின் செங்குத்துகள் அனைத்தும் சரிபார்க்கப்பட்ட காகிதத்தின் முனைகளில் உள்ளன - பலகோண கட்டக் கோடுகள் குறைந்தபட்சம் ஒரு பொதுவான புள்ளியை வெட்டுகின்றன.

சரிபார்க்கப்பட்ட காகிதத்தில் வரையப்பட்ட எந்த முக்கோணத்தின் பரப்பளவும், வரையப்பட்ட முக்கோணத்தின் செங்குத்துகள் வழியாக செல்லும் கட்டக் கோடுகளைப் பின்தொடர்ந்து செல்லும் வலது முக்கோணங்கள் மற்றும் செவ்வகங்களின் பகுதிகளின் கூட்டுத்தொகை அல்லது வேறுபாட்டின் மூலம் எளிதாகக் கணக்கிட முடியும்.

அத்தகைய பலகோணத்தின் பரப்பளவைக் கணக்கிட, நீங்கள் பின்வரும் தேற்றத்தைப் பயன்படுத்தலாம்:

தேற்றம் . விடுங்கள் - பலகோணத்திற்குள் உள்ள முழு எண் புள்ளிகளின் எண்ணிக்கை, - அதன் எல்லையில் உள்ள முழு எண் புள்ளிகளின் எண்ணிக்கை, - அதன் பகுதி. அப்புறம் நியாயம்தேர்வு சூத்திரம்:

உதாரணம். படத்தில் உள்ள பலகோணத்திற்குஎல் = 7 (சிவப்பு புள்ளிகள்), 9 (பச்சை புள்ளிகள்) அதனால்எஸ் = 7+ 9/2 -1 = 10,5 சதுர அலகுகள்.

தேர்வு தேற்றம்- உன்னதமான முடிவு மற்றும் .

முனைகளில் செங்குத்துகளைக் கொண்ட ஒரு முக்கோணத்தின் பரப்பளவு மற்றும் உள்ளே அல்லது பக்கங்களில் (செங்குத்துகளைத் தவிர) முனைகள் இல்லாதது 1/2 ஆகும். இந்த உண்மை.

3. வரலாறு

பிக்கின் ஃபார்முலாவை ஆஸ்திரிய கணிதவியலாளர் ஜார்ஜ் அலெக்சாண்டர் (1859-1942) கண்டுபிடித்தார். . 16 வயதில், ஜார்ஜ் பள்ளியில் பட்டம் பெற்றார் மற்றும் நுழைந்தார். 20 வயதில், இயற்பியல் மற்றும் கணிதம் கற்பிக்கும் உரிமையைப் பெற்றார். 1884 இல் பீக் புறப்பட்டார்செய்ய . அங்கு அவர் க்ளீனின் மற்றொரு மாணவரை சந்தித்தார்.. பின்னர், 1885 இல், அவர் திரும்பினார், அங்கு அவர் தனது விஞ்ஞான வாழ்க்கையை கழித்தார்.

ஜார்ஜ் பீக் ஐன்ஸ்டீனுடன் நட்பு கொண்டிருந்தார். பீக் மற்றும் ஐன்ஸ்டீன் பொதுவான அறிவியல் ஆர்வங்களைக் கொண்டிருந்தனர், ஆனால் இசையின் மீது ஆர்வமும் கொண்டிருந்தனர். பல்கலைக்கழகப் பேராசிரியர்கள் கொண்ட நால்வர் அணியில் விளையாடிய பிக், ஐன்ஸ்டீனை பிராகாவின் அறிவியல் மற்றும் இசைச் சங்கங்களுக்கு அறிமுகப்படுத்தினார்.

பீக்கின் கணித ஆர்வங்களின் வரம்பு மிகவும் பரந்ததாக இருந்தது. குறிப்பாக, அவர்களிடம் 50க்கும் மேற்பட்ட அறிவியல் ஆவணங்கள் உள்ளன. 1899 இல் அவரால் கண்டுபிடிக்கப்பட்ட பலகோணத்தின் பரப்பளவைக் கணக்கிடுவதற்கான பிக்ஸ் தேற்றம் பரவலாக அறியப்பட்டது. ஜெர்மனியில், இந்த தேற்றம் பள்ளி பாடப்புத்தகங்களில் சேர்க்கப்பட்டுள்ளது.

4.தேர்வு சூத்திரத்தின் பயன்பாடுகள்

பிக்ஸின் சூத்திரம் பலகோணங்களின் பகுதிகளைக் கணக்கிடுவதற்கு மட்டுமல்ல, ஒலிம்பியாட் மட்டத்தில் பல சிக்கல்களைத் தீர்க்கவும் பயன்படுத்தப்படுகிறது.

சிக்கல்களைத் தீர்க்கும் போது தேர்வு சூத்திரத்தைப் பயன்படுத்துவதற்கான சில எடுத்துக்காட்டுகள்:

1) சதுரங்க மன்னன் 8 × 8 செல்கள் கொண்ட பலகையைச் சுற்றி நடந்தான், ஒவ்வொன்றையும் பார்வையிட்டான்

வீட்டுக் களம் சரியாக ஒரு முறை மற்றும் கடைசி நகர்வின் மூலம் அசல் நிலைக்குத் திரும்புகிறது

களம். வயல்களின் மையங்களை வரிசையாக இணைக்கும் உடைந்த கோடு

ராஜாவை கடந்து சென்றது, சுய வெட்டுக்கள் இல்லை. எந்த பகுதியில் முடியும்

இந்த உடைந்த கோட்டைக் கட்டுப்படுத்தவா? (கலத்தின் பக்கம் 1.)

பீக்கின் சூத்திரத்தில் இருந்து, லோ-ஆல் வரையறுக்கப்பட்ட பகுதி என்பதை உடனடியாகப் பின்தொடர்கிறது.

மனா, 64/2 - 1 = 31 க்கு சமம்; இங்கே லட்டு முனைகள் மையங்கள் 64

புலங்கள் மற்றும் நிபந்தனையின்படி, அவை அனைத்தும் பலகோணத்தின் எல்லையில் உள்ளன. எனவே

எனவே, ராஜாவின் இதுபோன்ற "பாதைகள்" நிறைய இருந்தாலும், அவை அனைத்தும்

சம பகுதிகளின் பிணைக்கப்பட்ட பலகோணங்கள்.

மாநிலத் தேர்வு நிறுவனம் மற்றும் ஒருங்கிணைந்த மாநிலத் தேர்வின் சோதனை மற்றும் அளவீட்டுப் பொருட்களிலிருந்து பணிகள்

பணி B3

1 செமீ 1 செமீ செல் அளவு கொண்ட செக்கர்ஸ் பேப்பரில் சித்தரிக்கப்பட்டுள்ள உருவத்தின் பகுதியைக் கண்டறியவும் (படத்தைப் பார்க்கவும்). உங்கள் பதிலை சதுர சென்டிமீட்டரில் கொடுங்கள்.

4.முடிவு

ஆராய்ச்சி செயல்பாட்டின் போது, ​​நான் குறிப்பு மற்றும் பிரபலமான அறிவியல் இலக்கியங்களைப் படித்தேன். கிரிட் முனைகளில் செங்குத்துகளைக் கொண்ட பலகோணத்தின் பகுதியைக் கண்டறிவதில் உள்ள சிக்கல், 1899 ஆம் ஆண்டில் ஆஸ்திரியக் கணிதவியலாளர் பீக்கைக் குறிப்பிடத்தக்க பீக் சூத்திரத்தை நிரூபிக்கத் தூண்டியது என்பதை நான் அறிந்தேன்.

எனது பணியின் விளைவாக, சரிபார்க்கப்பட்ட காகிதத்தில் சிக்கல்களைத் தீர்ப்பது பற்றிய எனது அறிவை விரிவுபடுத்தினேன், படிப்பின் கீழ் உள்ள சிக்கல்களின் வகைப்பாட்டைத் தீர்மானித்தேன், மேலும் அவற்றின் பன்முகத்தன்மையை நம்பினேன்.

ஒரு சரிபார்க்கப்பட்ட காகிதத்தில் வரையப்பட்ட பலகோணங்களின் பகுதிகளை கணக்கிட கற்றுக்கொண்டேன், கருத்தில் கொள்ளப்பட்ட பணிகள் வெவ்வேறு நிலைகளில் உள்ளன - எளிமையானது முதல் ஒலிம்பியாட் வரை. ஒவ்வொருவரும் அவர்களிடையே சாத்தியமான அளவிலான சிக்கலான பணிகளைக் காணலாம், அதிலிருந்து தொடங்கி மிகவும் கடினமானவற்றைத் தீர்ப்பதற்குச் செல்ல முடியும்.

எனக்கு ஆர்வமுள்ள தலைப்பு மிகவும் பன்முகத்தன்மை வாய்ந்தது, சரிபார்க்கப்பட்ட காகிதத்தில் உள்ள சிக்கல்கள் வேறுபட்டவை, அவற்றைத் தீர்ப்பதற்கான முறைகள் மற்றும் நுட்பங்களும் வேறுபட்டவை என்ற முடிவுக்கு வந்தேன். எனவே, இந்த திசையில் தொடர்ந்து பணியாற்ற முடிவு செய்தோம்.

5. பயன்படுத்தப்பட்ட இலக்கியம்:

1. Vasil'ev N. B. பிக் சூத்திரத்தைச் சுற்றி // குவாண்டம். - 1974. - எண். 12

2. K o k e P r a s o l o v V. V. பிளானிமெட்ரியில் உள்ள சிக்கல்கள். - எம்.: MTsNMO, 2006.t e r G.S.M. வடிவவியலின் அறிமுகம். - எம்.: அறிவியல், 1966

3.ரோஸ்லோவா எல்.ஓ., ஷரிகின் ஐ.எஃப். அளவீடுகள். - எம்.: பப்ளிஷிங் ஹவுஸ். "திறந்த உலகம்", 2005.

இணைய வளங்கள்:

:

பணிக்கான கருத்து

"விமானத்தின் உருவங்களின் பகுதிகளின் கணக்கீடு. தேர்வு முறை"

இந்த தலைப்பைக் கருத்தில் கொள்வது மாணவரின் அறிவாற்றல் செயல்பாட்டை அதிகரிக்கும், அவர் பின்னர் வடிவியல் பாடங்களில் வரைபடத்தின் இணக்கத்தைக் காணத் தொடங்குவார் மற்றும் வடிவவியலை (மற்றும் பொதுவாக கணிதம்) ஒரு சலிப்பான அறிவியலாக உணருவதை நிறுத்துவார்.

ஒரு கணித ஆசிரியரால் மதிப்பாய்வு செய்யப்பட்டது

கோடிரேவா டாட்டியானா ஜார்ஜீவ்னா