Številni procesi, ki se dogajajo v naravi in tehnologiji, se v določenih intervalih ponavljajo. Takšni procesi se imenujejo periodični in so matematično opisani s periodičnimi funkcijami. Takšne funkcije vključujejo greh(x) , cos(x) , greh(wx), cos(wx) . Vsota dveh periodičnih funkcij, na primer funkcija oblike , na splošno ni več periodičen. Lahko pa se dokaže, da če razmerje w 1 / w 2 je racionalno število, potem je ta vsota periodična funkcija.
Najenostavnejše periodične procese – harmonična nihanja – opisujejo periodične funkcije greh(wx) in cos(wx). Bolj zapletene periodične procese opisujejo funkcije, sestavljene bodisi iz končnega ali neskončnega števila členov oblike greh(wx) in cos(wx).
3.2. Trigonometrične serije. Fourierjevi koeficienti
Oglejmo si funkcionalno serijo oblike:
Ta serija se imenuje trigonometrična; številke A 0 , b 0 , a 1 , b 1 ,A 2 , b 2 …, a n , b n ,… se imenujejo koeficientov trigonometrične vrste. Serija (1) je pogosto zapisana na naslednji način:
.
(2)
Ker imajo členi trigonometrične vrste (2) skupno periodo 
, potem je tudi vsota niza, če konvergira, periodična funkcija s periodo 
.
Predpostavimo, da funkcija f(x) je vsota te serije:
.
(3)
V tem primeru pravijo, da funkcija f(x)
se razširi v trigonometrično vrsto. Ob predpostavki, da ta niz enakomerno konvergira na intervalu 
, lahko njegove koeficiente določite z uporabo formul:
, 
,
.
(4)
Koeficienti nizov, določenih s temi formulami, se imenujejo Fourierjevi koeficienti.
Trigonometrične vrste (2), katerih koeficienti so določeni s Fourierjevimi formulami (4), se imenujejo blizu Fourierja, ki ustreza funkciji f(x).
Torej, če je periodična funkcija f(x) je vsota konvergentne trigonometrične vrste, potem je ta vrsta njena Fourierjeva vrsta.
3.3. Konvergenca Fourierjevih vrst
Formule (4) kažejo, da je mogoče Fourierjeve koeficiente izračunati za katero koli integrabilo na intervalu 
-periodična funkcija, tj. Za takšno funkcijo lahko vedno sestavite Fourierjev niz. Toda ali bo ta serija konvergirala k funkciji f(x)
in pod kakšnimi pogoji?
Spomnimo se, da funkcija f(x), definirana na segmentu [ a; b] , imenujemo delno gladko, če imata in njen derivat največ končno število diskontinuitetnih točk prve vrste.
Naslednji izrek daje zadostne pogoje za razgradljivost funkcije v Fourierjev niz.
Dirichletov izrek.
Naj 
-periodična funkcija f(x)
je po delih gladka 
. Potem se njegova Fourierjeva vrsta konvergira v f(x)
na vsaki njeni točki kontinuitete in na vrednost 0,5(f(x+0)+
f(x-0))
na prelomni točki.
Primer 1.
Razširite funkcijo v Fourierjev niz f(x)=
x, določeno na intervalu 
.
rešitev. Ta funkcija izpolnjuje Dirichletove pogoje in jo je zato mogoče razširiti v Fourierjev niz. Uporaba formul (4) in metode integracije po delih 
, poiščimo Fourierjeve koeficiente:
Torej Fourierjeva vrsta za funkcijo f(x) ima pogled.
Ki so že precej dolgočasne. In čutim, da je prišel trenutek, ko je čas, da iz strateških zalog teorije izvlečemo nove konzerve. Ali je mogoče kako drugače razširiti funkcijo v niz? Na primer, izrazite odsek ravne črte s sinusi in kosinusi? Zdi se neverjetno, a tako na videz oddaljene funkcije so lahko
"ponovna združitev". Poleg znanih diplom v teoriji in praksi obstajajo tudi drugi pristopi za razširitev funkcije v vrsto.
V tej lekciji se bomo seznanili s trigonometrično Fourierjevo vrsto, se dotaknili vprašanja njene konvergence in vsote ter seveda analizirali številne primere razširitve funkcij v Fourierjevo vrsto. Članek sem iskreno želel poimenovati "Fourierjevi nizi za telebane", vendar bi bilo to neiskreno, saj bi reševanje problemov zahtevalo poznavanje drugih vej matematične analize in nekaj praktičnih izkušenj. Zato bo preambula podobna treningu astronavtov =)
Najprej se morate lotiti preučevanja materialov strani v odlični obliki. Naspani, spočiti in trezni. Brez močnih čustev ob zlomljeni hrčkovi nogi in obsesivnih misli o tegobah življenja akvarijskih rib. Fourierjeve serije ni težko razumeti, vendar praktične naloge preprosto zahtevajo večjo koncentracijo pozornosti - v idealnem primeru bi se morali popolnoma ločiti od zunanjih dražljajev. Situacijo otežuje dejstvo, da ni preprostega načina za preverjanje rešitve in odgovora. Torej, če je vaše zdravje podpovprečno, potem je bolje narediti nekaj preprostejšega. Ali je res.
Drugič, pred poletom v vesolje je treba preučiti instrumentno ploščo vesoljskega plovila. Začnimo z vrednostmi funkcij, ki jih je treba klikniti na stroju:
Za katero koli naravno vrednoto:
1) . Dejansko sinusoida "prešije" os x skozi vsak "pi":
. V primeru negativnih vrednosti argumenta bo rezultat seveda enak: .
2) . A vsi tega niso vedeli. Kosinus "pi" je enakovreden "blinkerju":
Negativni argument ne spremeni stvari: 
.
Morda je to dovolj.
In tretjič, dragi kozmonavtski zbor, morate biti sposobni ... integrirati.
Predvsem samozavestno podstavi funkcijo pod diferencialni predznak, integrirati po delih in bodite v miru z Newton-Leibnizova formula. Začnimo s pomembnimi vajami pred poletom. Kategorično ne priporočam, da ga preskočite, da kasneje ne bi zmečkali v breztežnosti:
Primer 1
Izračunajte določene integrale
kjer zajema naravne vrednote.
rešitev: integracija se izvede nad spremenljivko "x" in na tej stopnji se diskretna spremenljivka "en" obravnava kot konstanta. V vseh integralih funkcijo postavimo pod diferencialni znak:
Kratka različica rešitve, ki bi jo bilo dobro ciljati, izgleda takole:
Navadimo se:
Štiri preostale točke so vaše. Poskusi se naloge lotiti vestno in integrale zapisati na kratek način. Vzorčne rešitve na koncu lekcije.
Po izvedbi vaj KVALITETNO si oblečemo skafandre
in se pripravljam na začetek!
Razširitev funkcije v Fourierjev niz na intervalu
Razmislite o tej funkciji odločen vsaj za določen čas (in morda za daljše obdobje). Če je ta funkcija integrabilna na intervalu, jo lahko razširimo v trigonometrijo Fourierjeve vrste:
, kjer so t.i Fourierjevi koeficienti.
V tem primeru se kliče številka obdobje razgradnje, številka pa je razpolovna doba razgradnje.
Očitno je, da je v splošnem primeru Fourierjeva vrsta sestavljena iz sinusov in kosinusov: 
Res, zapišimo podrobno:
Ničelni člen niza je običajno zapisan v obliki .
Fourierjevi koeficienti se izračunajo po naslednjih formulah: 
Povsem dobro razumem, da tistim, ki so začeli preučevati temo, še vedno niso jasni novi izrazi: obdobje razgradnje, pol cikla, Fourierjevi koeficienti itd. Brez panike, to ni primerljivo z navdušenjem pred odhodom v vesolje. Razumejmo vse v naslednjem primeru, pred izvedbo katerega je logično zastaviti pereča praktična vprašanja:
Kaj morate narediti pri naslednjih nalogah?
Razširite funkcijo v Fourierjev niz. Poleg tega je pogosto treba upodobiti graf funkcije, graf vsote niza, delno vsoto, v primeru prefinjenih profesorskih domislic narediti še kaj.
Kako razširiti funkcijo v Fourierjev niz?
V bistvu morate najti Fourierjevi koeficienti, torej sestavi in izračunaj tri določen integral.
Prepišite splošno obliko Fourierove vrste in tri delovne formule v svoj zvezek. Zelo sem vesel, da nekateri obiskovalci strani uresničujejo svoje otroške sanje in postanejo astronavti tik pred mojimi očmi =)
Primer 2
Razširite funkcijo v Fourierjev niz na intervalu. Zgradite graf, graf vsote niza in delne vsote.
rešitev: Prvi del naloge je razširitev funkcije v Fourierjev niz.
Začetek je standarden, ne pozabite zapisati, da:
V tem problemu je ekspanzijska doba polperioda.
Razširimo funkcijo v Fourierjev niz na intervalu: 
Z ustreznimi formulami najdemo Fourierjevi koeficienti. Zdaj moramo sestaviti in izračunati tri določen integral. Za udobje bom točke oštevilčil:
1) Prvi integral je najenostavnejši, vendar zahteva tudi zrkla: 
2) Uporabite drugo formulo:
Ta integral je dobro znan in jemlje kos za kosom: 
Uporabljeno, ko se najde metoda subsumiranja funkcije pod diferencialni predznak.
Pri obravnavani nalogi je bolj priročno takoj uporabiti formula za integracijo po delih v določenem integralu 
:
Nekaj tehničnih opomb. Prvič, po uporabi formule celoten izraz mora biti v velikih oklepajih, ker obstaja konstanta pred prvotnim integralom. Ne izgubimo je! Oklepaje je mogoče razširiti v katerem koli nadaljnjem koraku; to sem naredil kot zadnjo možnost. V prvem "delu" 
Pri zamenjavi smo izredno previdni, kot vidite, konstanta ni uporabljena, meje integracije pa so vstavljene v izdelek. To dejanje je označeno v oglatih oklepajih. No, integral drugega “delčka” formule iz vadbene naloge poznate;-)
In kar je najpomembnejše – izjemna koncentracija!
3) Iščemo tretji Fourierjev koeficient:
Dobimo relativno prejšnjega integrala, ki je tudi integrira po delih:
Ta primer je nekoliko bolj zapleten, korak za korakom bom komentiral nadaljnje korake: 
(1) Izraz je v celoti zaprt v velikih oklepajih. Nisem hotel izpasti dolgočasen, prepogosto izgubijo konstanto.
(2) V tem primeru sem takoj odprl te velike oklepaje. Posebna pozornost Posvetimo se prvemu »kosu«: konstanta kadi ob strani in ne sodeluje pri zamenjavi meja vključevanja (in) v izdelek. Zaradi natrpanosti zapisa je ponovno priporočljivo to dejanje označiti z oglatimi oklepaji. Z drugim "kosom" 
vse je preprostejše: tukaj se je ulomek pojavil po odprtju velikih oklepajev in konstanta - kot rezultat integracije znanega integrala;-)
(3) V oglatem oklepaju izvedemo transformacije, v desnem integralu pa nadomestimo limite integracije.
(4) Iz oglatih oklepajev odstranimo “utripajočo luč”: , nato pa odpremo notranje oklepaje: .
(5) Prekličemo 1 in –1 v oklepajih in naredimo končne poenostavitve.
Končno so najdeni vsi trije Fourierjevi koeficienti: 
Vstavimo jih v formulo 
:
Hkrati ne pozabite razdeliti na pol. Na zadnjem koraku se konstanta (»minus dva«), ki ni odvisna od »en«, vzame izven vsote.
Tako smo dobili razširitev funkcije v Fourierjev niz na intervalu: 
Preučimo vprašanje konvergence Fourierjevega niza. Razložil bom predvsem teorijo Dirichletov izrek, dobesedno "na prste", zato, če potrebujete stroge formulacije, si oglejte učbenik o matematični analizi (na primer 2. zvezek Bohana; ali 3. zvezek Fichtenholtza, vendar je težje).
Drugi del naloge zahteva risanje grafa, grafa vsote serije in grafa delne vsote.
Graf funkcije je običajen premica na ravnini, ki je narisana s črno pikčasto črto: 
Ugotovimo vsoto serije. Kot veste, funkcijske vrste konvergirajo k funkcijam. V našem primeru konstruirana Fourierjeva vrsta 
za katero koli vrednost "x" bo konvergirala k funkciji, ki je prikazana rdeče. Ta funkcija tolerira rupture 1. vrste na točkah, ampak je na njih tudi definiran (rdeče pike na risbi)
Torej: 
. Preprosto je videti, da se opazno razlikuje od prvotne funkcije, zato v vnosu 
Namesto znaka enačaja se uporablja tilda.
Preučimo algoritem, ki je primeren za sestavo vsote serije.
Na osrednjem intervalu Fourierjeva vrsta konvergira k sami funkciji (osrednji rdeči segment sovpada s črno pikčasto črto linearne funkcije).
Zdaj pa se pogovorimo malo o naravi obravnavane trigonometrične ekspanzije. Fourierjeve vrste 
vključene so le periodične funkcije (konstanta, sinusi in kosinusi), torej vsota serije 
je tudi periodična funkcija.
Kaj to pomeni v našem konkretnem primeru? In to pomeni, da je vsota serije 
–vsekakor periodično in rdeči segment intervala se mora neskončno ponavljati na levi in desni.
Mislim, da je pomen besedne zveze "obdobje razgradnje" zdaj končno postal jasen. Preprosto povedano, vsakič znova se situacija ponovi.
V praksi običajno zadošča, da prikažemo tri obdobja razgradnje, kot je to narejeno na risbi. No, in tudi "štori" sosednjih obdobij - tako da je jasno, da se graf nadaljuje.
Posebej zanimivi so diskontinuitetne točke 1. vrste. Na takšnih točkah Fourierjeva vrsta konvergira k izoliranim vrednostim, ki se nahajajo točno na sredini »skoka« diskontinuitete (rdeče pike na risbi). Kako najti ordinato teh točk? Najprej poiščemo ordinato »zgornjega nadstropja«: za to izračunamo vrednost funkcije na skrajni desni točki osrednje periode raztezanja: . Za izračun ordinate »spodnjega nadstropja« je najlažje vzeti skrajno levo vrednost istega obdobja: 
. Ordinata povprečne vrednosti je aritmetična sredina vsote "zgoraj in spodaj": . Prijetno dejstvo je, da boste pri sestavljanju risbe takoj videli, ali je sredina izračunana pravilno ali nepravilno.
Konstruirajmo delno vsoto vrste in hkrati ponovimo pomen izraza "konvergenca". Motiv je znan tudi iz lekcije o vsota številske serije. Naj podrobneje opišemo naše bogastvo:
Če želite sestaviti delno vsoto, morate napisati nič + še dva člana serije. to je
Na risbi je graf funkcije prikazan v zeleni barvi in, kot vidite, precej tesno »ovije« celotno vsoto. Če upoštevamo delno vsoto petih členov serije, bo graf te funkcije še natančneje približal rdeče črte; če je sto članov, se bo "zelena kača" dejansko popolnoma združila z rdečimi segmenti, itd. Tako Fourierjeva vrsta konvergira k svoji vsoti.
Zanimivo je, da je vsak delni znesek neprekinjena funkcija, vendar je skupna vsota serije še vedno diskontinuirana.
V praksi ni tako redko zgraditi graf delne vsote. Kako to narediti? V našem primeru je treba upoštevati funkcijo na segmentu, izračunati njene vrednosti na koncih segmenta in na vmesnih točkah (več točk upoštevate, bolj natančen bo graf). Nato označite te točke na risbi in skrbno narišite graf na periodo, nato pa ga "replicirajte" v sosednje intervale. Kako drugače? Navsezadnje je tudi približek periodična funkcija... ...na nek način me njegov graf spominja na enakomeren srčni ritem na zaslonu medicinske naprave.
Izvajanje konstrukcije seveda ni zelo priročno, saj morate biti zelo previdni in ohraniti natančnost najmanj pol milimetra. Vendar pa bom razveselil bralce, ki jim risanje ni všeč - v "pravem" problemu ni vedno potrebno izvesti risanje; v približno 50% primerov je treba funkcijo razširiti v Fourierjev niz in to je to .
Po končani risbi opravimo nalogo:
Odgovori: 
Pri številnih nalogah trpi funkcija ruptura 1. vrste ravno v obdobju razgradnje:
Primer 3
Razširite funkcijo, podano na intervalu, v Fourierjev niz. Nariši graf funkcije in skupne vsote serije.
Predlagana funkcija je določena po delih (in, upoštevajte, samo na segmentu) in zdrži ruptura 1. vrste na točki. Ali je mogoče izračunati Fourierjeve koeficiente? Brez težav. Tako leva kot desna stran funkcije sta integrabilni na svojih intervalih, zato je treba integrale v vsaki od treh formul predstaviti kot vsoto dveh integralov. Poglejmo na primer, kako se to naredi za ničelni koeficient:
Izkazalo se je, da je drugi integral enak nič, kar je zmanjšalo delo, vendar ni vedno tako.
Druga dva Fourierjeva koeficienta sta opisana podobno.
Kako prikazati vsoto serije? Na levem intervalu narišemo odsek ravne črte, na intervalu pa odsek ravne črte (odsek osi označimo krepko in krepko). To pomeni, da na razteznem intervalu vsota serije sovpada s funkcijo povsod, razen v treh "slabih" točkah. Na točki diskontinuitete funkcije bo Fourierjeva vrsta konvergirala k izolirani vrednosti, ki se nahaja točno na sredini "skoka" diskontinuitete. Ustno ga ni težko videti: leva meja: , desna meja: 
in očitno je ordinata sredine 0,5.
Zaradi periodičnosti vsote je treba sliko »pomnožiti« na sosednje periode, predvsem pa mora biti ista stvar upodobljena na intervalih in . Istočasno bo Fourierjeva vrsta v točkah konvergirala k srednjim vrednostim.
Pravzaprav tu ni nič novega.
Poskusite se sami spopasti s to nalogo. Približni vzorec končnega dizajna in risba na koncu lekcije.
Razširitev funkcije v Fourierjev niz za poljubno periodo
Za poljubno raztezno obdobje, kjer je "el" katero koli pozitivno število, se formule za Fourierjev niz in Fourierjeve koeficiente razlikujejo po nekoliko bolj zapletenem argumentu za sinus in kosinus:
Če , potem dobimo intervalne formule, s katerimi smo začeli.
Algoritem in principi reševanja problema so popolnoma ohranjeni, vendar se tehnična zapletenost izračunov poveča:
Primer 4
Razširite funkcijo v Fourierjev niz in narišite vsoto. 
rešitev: pravzaprav analog primera št. 3 z ruptura 1. vrste na točki. V tem problemu je ekspanzijska doba polperioda. Funkcija je definirana le na polintervalu, vendar to ne spremeni stvari - pomembno je, da sta oba dela funkcije integrabilna.
Razširimo funkcijo v Fourierjev niz:
Ker je funkcija v izvoru diskontinuirana, je treba vsak Fourierjev koeficient očitno zapisati kot vsoto dveh integralov:
1) Čim bolj podrobno bom zapisal prvi integral:
2) Pazljivo pogledamo površino Lune:
Drugi integral vzemite kos za kosom:
Na kaj moramo biti zelo pozorni, ko odpremo nadaljevanje rešitve z zvezdico?
Prvič, ne izgubimo prvega integrala 
, kjer takoj izvedemo pripisovanje diferencialnemu predznaku. Drugič, ne pozabite na nesrečno konstanto pred velikimi oklepaji in naj vas znaki ne zmedejo pri uporabi formule 
. Velike oklepaje je še vedno bolj priročno odpreti takoj v naslednjem koraku.
Ostalo je stvar tehnike, težave lahko povzročijo le premajhne izkušnje pri reševanju integralov.
Da, niso bili zaman ugledni kolegi francoskega matematika Fourierja ogorčeni - kako si je upal urediti funkcije v trigonometrične serije?! =) Mimogrede, verjetno vse zanima praktični pomen zadevne naloge. Fourier je sam delal na matematičnem modelu toplotne prevodnosti, nato pa se je niz, poimenovan po njem, začel uporabljati za preučevanje številnih periodičnih procesov, ki so vidni in nevidni v okoliškem svetu. Zdaj sem se mimogrede ujel, da nisem slučajno primerjal grafa drugega primera s periodičnim ritmom srca. Zainteresirani se lahko seznanijo s praktično uporabo Fourierjeva transformacija v virih tretjih oseb. ...Čeprav je bolje, da ne - zapomnili si ga bomo kot prvo ljubezen =)
3) Ob upoštevanju večkrat omenjenih šibkih členov poglejmo tretji koeficient:
Integrirajmo po delih: 
Najdene Fourierjeve koeficiente nadomestimo v formulo 
, ne da bi pozabili razdeliti ničelni koeficient na polovico:
Narišimo vsoto serije. Na kratko ponovimo postopek: na intervalu zgradimo premico, na intervalu pa premico. Če je vrednost "x" enaka nič, postavimo točko na sredino "skoka" vrzeli in "repliciramo" graf za sosednja obdobja: 
Na "stičiščih" obdobij bo vsota enaka tudi srednjim točkam "skoka" vrzeli.
pripravljena Naj vas spomnim, da je sama funkcija po pogoju definirana samo na polintervalu in očitno sovpada z vsoto serije na intervalih
Odgovori:
Včasih je delno podana funkcija zvezna v obdobju raztezanja. Najenostavnejši primer: 
. rešitev (glej Bohan zvezek 2) enako kot v prejšnjih dveh primerih: kljub kontinuiteta delovanja v točki je vsak Fourierjev koeficient izražen kot vsota dveh integralov.
Na intervalu razgradnje diskontinuitetne točke 1. vrste in/ali je lahko več "stičišč" grafa (dve, tri in na splošno katera koli dokončno količina). Če je funkcija integrabilna na vsakem delu, potem je tudi razširljiva v Fourierjevo vrsto. Toda iz praktičnih izkušenj se ne spomnim tako krute stvari. Vendar pa obstajajo težje naloge od pravkar obravnavanih in na koncu članka so povezave do Fourierjevih vrst povečane kompleksnosti za vsakogar.
Medtem pa se sprostimo, naslonimo na svoje stole in opazujmo neskončna prostranstva zvezd:
Primer 5
Razširite funkcijo v Fourierjev niz na intervalu in narišite vsoto niza.
V tem problemu funkcija neprekinjeno na razteznem polintervalu, kar poenostavi rešitev. Vse je zelo podobno kot v primeru št. 2. Iz vesoljske ladje ni pobega - odločiti se boste morali =) Približen vzorec oblikovanja na koncu lekcije, urnik je priložen.
Razširitev sodih in lihih funkcij v Fourierjev niz
S sodimi in lihimi funkcijami je postopek reševanja problema opazno poenostavljen. In tukaj je razlog. Vrnimo se k razširitvi funkcije v Fourierjev niz s periodo "dva pi" 
in poljubna pika "dva el" 
.
Predpostavimo, da je naša funkcija soda. Splošni člen niza, kot lahko vidite, vsebuje sode kosinuse in lihe sinuse. In če razširjamo funkcijo EVEN, zakaj potem potrebujemo lihe sinuse?! Ponastavimo nepotreben koeficient: .
torej sodo funkcijo lahko razširimo v Fourierjev niz le v kosinusih:
Ker integrali sodih funkcij vzdolž segmenta integracije, ki je simetričen glede na nič, se lahko podvoji, nato pa se preostali Fourierjevi koeficienti poenostavijo.
Za vrzel: 
Za poljuben interval: 
Primeri učbenikov, ki jih lahko najdete v skoraj vseh učbenikih matematične analize, vključujejo razširitve sodih funkcij 
. Poleg tega sem jih večkrat srečal v svoji osebni praksi:
Primer 6
Funkcija je dana. Zahtevano:
1) razširite funkcijo v Fourierjev niz s periodo , kjer je poljubno pozitivno število;
2) zapišite razširitev na interval, sestavite funkcijo in grafično sestavite skupno vsoto niza.
rešitev: v prvem odstavku je predlagana rešitev problema v splošni obliki in to je zelo priročno! Če se pojavi potreba, samo nadomestite svojo vrednost.
1) V tem problemu je ekspanzijska doba polperioda. Med nadaljnjimi dejanji, zlasti med integracijo, se "el" šteje za konstanto
Funkcija je soda, kar pomeni, da jo je mogoče razširiti v Fourierjev niz le v kosinusih: 
.
Fourierjeve koeficiente iščemo s pomočjo formul 
. Bodite pozorni na njihove brezpogojne prednosti. Prvič, integracija je izvedena na pozitivnem segmentu razširitve, kar pomeni, da se varno znebimo modula 
, upoštevajoč samo "X" od obeh kosov. In drugič, integracija je opazno poenostavljena.
dva: 
Integrirajmo po delih:
Torej:
, medtem ko je konstanta , ki ni odvisna od “en”, vzeta izven vsote.
Odgovori: 
2) Zapišimo razširitev na intervalu, zamenjamo zahtevano polperiodo v splošno formulo:
Fourierjeve vrste so predstavitev poljubne funkcije z določeno periodo v obliki vrste. Na splošno se ta rešitev imenuje dekompozicija elementa vzdolž ortogonalne baze. Razširitev funkcij v Fourierjev niz je dokaj močno orodje za reševanje različnih problemov zaradi lastnosti te transformacije med integracijo, diferenciacijo, pa tudi premikanjem izrazov z argumentom in konvolucijo.
Oseba, ki ni seznanjena z višjo matematiko, pa tudi z deli francoskega znanstvenika Fourierja, najverjetneje ne bo razumela, kaj so te "serije" in za kaj so potrebne. Medtem je ta preobrazba postala precej integrirana v naša življenja. Ne uporabljajo ga le matematiki, ampak tudi fiziki, kemiki, zdravniki, astronomi, seizmologi, oceanografi in mnogi drugi. Oglejmo si pobliže tudi dela velikega francoskega znanstvenika, ki je prišel do odkritja, ki je bilo pred svojim časom.
Človek in Fourierjeva transformacija
Fourierove vrste so ena od metod (skupaj z analizo in drugimi). Ta proces se zgodi vsakič, ko oseba sliši zvok. Naše uho samodejno transformira osnovne delce v elastičnem mediju v vrste (vzdolž spektra) zaporednih stopenj glasnosti za tone različnih višin. Nato možgani te podatke spremenijo v zvoke, ki so nam znani. Vse to se zgodi brez naše želje ali zavesti, samo od sebe, a da bi razumeli te procese, bo potrebnih nekaj let študija višje matematike.
Več o Fourierjevi transformaciji
Fourierjevo transformacijo je mogoče izvesti z analitičnimi, numeričnimi in drugimi metodami. Fourierjeve vrste se nanašajo na numerično metodo razgradnje kakršnih koli nihajnih procesov - od oceanskih plim in svetlobnih valov do ciklov sončne (in drugih astronomskih objektov) aktivnosti. Z uporabo teh matematičnih tehnik lahko analizirate funkcije, ki predstavljajo vse nihajne procese kot niz sinusnih komponent, ki se premikajo od minimuma do maksimuma in nazaj. Fourierjeva transformacija je funkcija, ki opisuje fazo in amplitudo sinusoide, ki ustreza določeni frekvenci. Ta proces se lahko uporablja za reševanje zelo kompleksnih enačb, ki opisujejo dinamične procese, ki nastanejo pod vplivom toplotne, svetlobne ali električne energije. Poleg tega Fourierjeve vrste omogočajo izolacijo konstantnih komponent v kompleksnih oscilacijskih signalih, kar omogoča pravilno interpretacijo eksperimentalnih opazovanj, pridobljenih v medicini, kemiji in astronomiji.
Zgodovinsko ozadje
Ustanovitelj te teorije je francoski matematik Jean Baptiste Joseph Fourier. Ta preobrazba je bila pozneje poimenovana po njem. Sprva je znanstvenik s svojo metodo preučeval in razlagal mehanizme toplotne prevodnosti - širjenje toplote v trdnih snoveh. Fourier je predlagal, da se lahko začetna nepravilna porazdelitev razgradi na preproste sinusoide, od katerih bo imela vsaka svoj temperaturni minimum in maksimum ter svojo fazo. V tem primeru bo vsaka taka komponenta izmerjena od minimuma do maksimuma in obratno. Matematična funkcija, ki opisuje zgornje in spodnje vrhove krivulje ter fazo vsakega od harmonikov, se imenuje Fourierjeva transformacija izraza porazdelitve temperature. Avtor teorije je splošno porazdelitveno funkcijo, ki jo je težko matematično opisati, reduciral na zelo priročno vrsto kosinusa in sinusa, ki skupaj dajeta prvotno porazdelitev.
Načelo preobrazbe in pogledi sodobnikov
Znanstvenikovi sodobniki - vodilni matematiki zgodnjega devetnajstega stoletja - te teorije niso sprejeli. Glavni ugovor je bila Fourierjeva trditev, da je diskontinuirano funkcijo, ki opisuje ravno črto ali diskontinuirano krivuljo, mogoče predstaviti kot vsoto sinusnih izrazov, ki so zvezni. Kot primer razmislite o Heavisideovem koraku: njegova vrednost je nič na levi strani diskontinuitete in ena na desni strani. Ta funkcija opisuje odvisnost električnega toka od začasne spremenljivke, ko je tokokrog sklenjen. Sodobniki takratne teorije se še nikoli niso srečali s podobno situacijo, kjer bi bil diskontinuiran izraz opisan s kombinacijo zveznih, navadnih funkcij, kot so eksponentna, sinusna, linearna ali kvadratna.
Kaj je zmedlo francoske matematike glede Fourierjeve teorije?
Navsezadnje, če je imel matematik prav v svojih izjavah, potem lahko s seštevanjem neskončnega trigonometričnega Fourierovega niza dobimo natančno predstavitev stopenjskega izraza, tudi če ima veliko podobnih korakov. Na začetku devetnajstega stoletja se je takšna izjava zdela absurdna. Toda kljub vsem dvomom so številni matematiki razširili obseg proučevanja tega pojava in ga presegli študij toplotne prevodnosti. Vendar pa je večino znanstvenikov še naprej mučilo vprašanje: "Ali se lahko vsota sinusne serije konvergira k natančni vrednosti diskontinuirane funkcije?"
Konvergenca Fourierjevih vrst: primer
Vprašanje konvergence se pojavi vedno, ko je treba sešteti neskončno vrsto števil. Da bi razumeli ta pojav, razmislite o klasičnem primeru. Vam bo kdaj uspelo doseči steno, če bo vsak naslednji korak za polovico manjši od prejšnjega? Recimo, da ste dva metra od tarče, prvi korak vas pripelje do polovice, naslednji do tričetrt, po petem pa boste prehodili skoraj 97 odstotkov poti. Vendar ne glede na to, koliko korakov naredite, ne boste dosegli zastavljenega cilja v strogem matematičnem smislu. Z uporabo numeričnih izračunov je mogoče dokazati, da se je na koncu mogoče približati na določeno razdaljo. Ta dokaz je enakovreden dokazovanju, da bo vsota polovice, ene četrtine itd. težila k enotnosti.
Vprašanje konvergence: Drugi prihod ali Naprava Lorda Kelvina
To vprašanje se je znova pojavilo ob koncu devetnajstega stoletja, ko so poskušali s Fourierjevimi vrstami napovedati intenzivnost plimovanja. V tem času je Lord Kelvin izumil instrument, ki je bil analogna računalniška naprava, ki je vojaškim in trgovskim mornarjem omogočala spremljanje tega naravnega pojava. Ta mehanizem je določil sklope faz in amplitud iz tabele višin plime in ustreznih časovnih točk, skrbno izmerjenih v danem pristanišču skozi vse leto. Vsak parameter je bil sinusna komponenta izraza višine plime in je bil ena od rednih komponent. Meritve so bile vnesene v računski instrument Lorda Kelvina, ki je sintetiziral krivuljo, ki je napovedala višino vode kot funkcijo časa za naslednje leto. Kmalu so se podobne krivulje izrisale za vsa pristanišča sveta.
Kaj pa, če je proces moten zaradi diskontinuirane funkcije?
Takrat se je zdelo očitno, da lahko napovedovalec plimskih valov z velikim številom elementov štetja izračuna veliko število faz in amplitud ter tako zagotovi natančnejše napovedi. Vendar se je izkazalo, da tega vzorca ni opaziti v primerih, ko je izraz plimovanja, ki bi ga bilo treba sintetizirati, vseboval oster skok, to je bil diskontinuiran. Če v napravo vnesemo podatke iz tabele časovnih trenutkov, ta izračuna več Fourierjevih koeficientov. Prvotna funkcija se obnovi zahvaljujoč sinusnim komponentam (v skladu z najdenimi koeficienti). Neskladje med izvirnim in rekonstruiranim izrazom je mogoče izmeriti na kateri koli točki. Pri ponovnih izračunih in primerjavah je jasno, da se vrednost največje napake ne zmanjša. Vendar so lokalizirani v območju, ki ustreza točki diskontinuitete, na kateri koli drugi točki pa težijo k ničli. Leta 1899 je ta rezultat teoretično potrdil Joshua Willard Gibbs z univerze Yale.
Konvergenca Fourierjevih vrst in razvoj matematike nasploh
Fourierjeva analiza ni uporabna za izraze, ki vsebujejo neskončno število konic v določenem intervalu. Na splošno Fourierjeva vrsta vedno konvergira, če je izvirna funkcija predstavljena z rezultatom dejanske fizikalne meritve. Vprašanja o konvergenci tega procesa za posebne razrede funkcij so privedla do nastanka novih vej v matematiki, na primer teorije posplošenih funkcij. Povezujejo jo z imeni, kot so L. Schwartz, J. Mikusinski in J. Temple. V okviru te teorije je bila ustvarjena jasna in natančna teoretična podlaga za izraze, kot sta Diracova delta funkcija (opisuje območje enega samega območja, koncentriranega v neskončno majhni okolici točke) in Heavisideov "korak". Zahvaljujoč temu delu so Fourierjeve vrste postale uporabne za reševanje enačb in problemov, ki vključujejo intuitivne pojme: točkasti naboj, točkasta masa, magnetni dipoli in koncentrirana obremenitev na žarku.
Fourierjeva metoda
Fourierjeve vrste se v skladu z načeli interference začnejo z razgradnjo kompleksnih oblik na preprostejše. Na primer, spremembo toplotnega toka razložimo s prehodom skozi različne ovire iz toplotnoizolacijskega materiala nepravilne oblike ali spremembo zemeljske površine - potres, spremembo orbite nebesnega telesa - vpliv planetov. Takšne enačbe, ki opisujejo preproste klasične sisteme, je praviloma enostavno rešiti za vsak posamezen val. Fourier je pokazal, da je mogoče preproste rešitve sešteti tudi za rešitve bolj zapletenih problemov. V matematičnem smislu so Fourierjevi nizi tehnika za predstavitev izraza kot vsote harmonikov - kosinusa in sinusa. Zato je ta analiza znana tudi kot "harmonična analiza".
Fourierjeva serija - idealna tehnika pred "računalniško dobo"
Pred nastankom računalniške tehnologije je bila Fourierjeva tehnika najboljše orožje v arzenalu znanstvenikov pri delu z valovno naravo našega sveta. Fourierjeva vrsta v kompleksni obliki omogoča reševanje ne le preprostih problemov, ki jih je mogoče neposredno uporabiti za Newtonove zakone mehanike, ampak tudi temeljnih enačb. Večino odkritij Newtonove znanosti v devetnajstem stoletju je omogočila le Fourierjeva tehnika.
Fourierjeva vrsta danes
Z razvojem računalnikov so se Fourierove transformacije dvignile na kakovostno novo raven. Ta tehnika je trdno uveljavljena na skoraj vseh področjih znanosti in tehnologije. Primer sta digitalni avdio in video. Njegovo izvajanje je postalo mogoče le zahvaljujoč teoriji, ki jo je razvil francoski matematik v začetku devetnajstega stoletja. Tako je Fourierjeva serija v kompleksni obliki omogočila preboj v študiju vesolja. Poleg tega je vplival na študij fizike polprevodniških materialov in plazme, mikrovalovne akustike, oceanografije, radarja in seizmologije.
Trigonometrična Fourierjeva vrsta
V matematiki je Fourierjeva vrsta način predstavitve poljubnih kompleksnih funkcij kot vsote enostavnejših. V splošnih primerih je lahko število takih izrazov neskončno. Poleg tega, bolj kot je njihovo število upoštevano pri izračunu, bolj natančen je končni rezultat. Najpogosteje se kot najenostavnejše uporabljajo trigonometrične funkcije kosinusa ali sinusa. V tem primeru se Fourierjeve vrste imenujejo trigonometrične, rešitev takih izrazov pa harmonična ekspanzija. Ta metoda igra pomembno vlogo v matematiki. Prvič, trigonometrične vrste zagotavljajo sredstvo za prikazovanje in tudi preučevanje funkcij; to je glavni aparat teorije. Poleg tega vam omogoča reševanje številnih problemov matematične fizike. Končno je ta teorija prispevala k razvoju in zaživela številne zelo pomembne veje matematične znanosti (teorija integralov, teorija periodičnih funkcij). Poleg tega je služil kot izhodišče za razvoj naslednjih funkcij realne spremenljivke in postavil temelje za harmonično analizo.
Funkcije, ki jih razgradijo na komponente. Izmenični tokovi in napetosti, pomiki, hitrosti in pospeški ročičnih mehanizmov ter akustični valovi so tipični praktični primeri uporabe periodičnih funkcij v inženirskih izračunih.
Razširitev v Fourierjev niz temelji na predpostavki, da je mogoče vse funkcije praktičnega pomena v intervalu -π ≤x≤ π izraziti v obliki konvergentnih trigonometričnih nizov (niz velja za konvergentnega, če je zaporedje delnih vsot, sestavljenih iz njegovih členov konvergira):
Standardni (=navadni) zapis skozi vsoto sinx in cosx
f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,
kjer so a o, a 1,a 2,...,b 1,b 2,.. realne konstante, tj.
Pri čemer so za območje od -π do π koeficienti Fourierjeve vrste izračunani po formulah:
Koeficienti a o , a n in b n se imenujejo Fourierjevi koeficienti, in če jih je mogoče najti, se pokliče serija (1). poleg Fourierja, ki ustreza funkciji f(x). Za niz (1) imenujemo člen (a 1 cosx+b 1 sinx) prvi oz osnovni harmonik,
Drug način za pisanje serije je uporaba relacije acosx+bsinx=csin(x+α)
f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)
Kjer je a o konstanta, c 1 =(a 1 2 +b 1 2) 1/2, c n =(a n 2 +b n 2) 1/2 so amplitude različnih komponent in je enako a n =arctg a n /b n.
Za vrsto (1) se člen (a 1 cosx+b 1 sinx) ali c 1 sin(x+α 1) imenuje prvi oz. osnovni harmonik,(a 2 cos2x+b 2 sin2x) ali c 2 sin(2x+α 2) se imenuje drugi harmonik in tako dalje.
Za natančno predstavitev kompleksnega signala je običajno potrebno neskončno število izrazov. Vendar je v mnogih praktičnih problemih dovolj, da upoštevamo samo prvih nekaj členov.
Fourierjeva vrsta neperiodičnih funkcij s periodo 2π.
Razširitev neperiodičnih funkcij v Fourierove vrste.
Če je funkcija f(x) neperiodična, to pomeni, da je ni mogoče razširiti v Fourierjev niz za vse vrednosti x. Vendar pa je mogoče definirati Fourierjev niz, ki predstavlja funkcijo v poljubnem območju širine 2π.
Glede na neperiodično funkcijo je mogoče konstruirati novo funkcijo tako, da izberete vrednosti f(x) znotraj določenega območja in jih ponovite zunaj tega območja v intervalih 2π. Ker je nova funkcija periodična s periodo 2π, jo je mogoče razširiti v Fourierjev niz za vse vrednosti x. Na primer, funkcija f(x)=x ni periodična. Če pa jo je treba razširiti v Fourierjev niz v intervalu od o do 2π, se izven tega intervala sestavi periodična funkcija s periodo 2π (kot je prikazano na spodnji sliki).
Za neperiodične funkcije, kot je f(x)=x, je vsota Fourierjevega niza enaka vrednosti f(x) v vseh točkah v danem območju, vendar ni enaka f(x) za točke izven obsega. Za iskanje Fourierjeve vrste neperiodične funkcije v območju 2π se uporablja ista formula Fourierjevih koeficientov.
Sode in lihe funkcije.
Pravijo, da je funkcija y=f(x) celo, če je f(-x)=f(x) za vse vrednosti x. Grafi sodih funkcij so vedno simetrični glede na os y (to pomeni, da so zrcalne slike). Dva primera sodih funkcij: y=x2 in y=cosx.
Pravijo, da je funkcija y=f(x) čudno,če je f(-x)=-f(x) za vse vrednosti x. Grafi lihih funkcij so vedno simetrični glede na izvor.
Mnoge funkcije niso niti sode niti lihe.
Razširitev v Fourierjev niz v kosinuse.
Fourierjeva vrsta sode periodične funkcije f(x) s periodo 2π vsebuje samo kosinusne člene (tj. brez sinusnih členov) in lahko vključuje konstanten člen. torej
kje so koeficienti Fourierove vrste,
Fourierjeva vrsta lihe periodične funkcije f(x) s periodo 2π vsebuje samo člene s sinusi (to pomeni, da ne vsebuje členov s kosinusi).
torej
kje so koeficienti Fourierove vrste,
Fourierjeva vrsta na pol cikla.
Če je funkcija definirana za obseg, recimo od 0 do π, in ne samo od 0 do 2π, jo je mogoče razširiti v vrsto samo v sinusih ali samo v kosinusih. Nastala Fourierjeva vrsta se imenuje blizu Fourierja na pol cikla.
Če želite dobiti razgradnjo Fourierjev polciklični kosinus funkcije f(x) v območju od 0 do π, potem je treba zgraditi sodo periodično funkcijo. Na sl. Spodaj je funkcija f(x)=x, zgrajena na intervalu od x=0 do x=π. Ker je soda funkcija simetrična glede na os f(x), narišemo premico AB, kot je prikazano na sliki. spodaj. Če predpostavimo, da je zunaj obravnavanega intervala nastala trikotna oblika periodična s periodo 2π, potem končni graf izgleda takole: na sl. spodaj. Ker moramo kot prej pridobiti Fourierjevo razširitev v kosinusih, izračunamo Fourierjeva koeficienta a o in a n
Če želite dobiti funkcije f(x) v območju od 0 do π, potem morate sestaviti liho periodično funkcijo. Na sl. Spodaj je funkcija f(x)=x, zgrajena na intervalu od x=0 do x=π. Ker je liha funkcija simetrična glede na izvor, sestavimo premico CD, kot je prikazano na sl. Če predpostavimo, da je zunaj obravnavanega intervala nastali žagasti signal periodičen s periodo 2π, potem ima končni graf obliko, prikazano na sl. Ker moramo kot prej dobiti Fourierjevo razširitev polcikla v smislu sinusov, izračunamo Fourierjev koeficient. b
Fourierjeva vrsta za poljuben interval.
Razširitev periodične funkcije s periodo L.
Periodična funkcija f(x) se ponavlja, ko x narašča za L, tj. f(x+L)=f(x). Prehod s predhodno obravnavanih funkcij s periodo 2π na funkcije s periodo L je dokaj preprost, saj ga lahko izvedemo s spremembo spremenljivke.
Za iskanje Fourierjeve vrste funkcije f(x) v območju -L/2≤x≤L/2 uvedemo novo spremenljivko u, tako da ima funkcija f(x) periodo 2π glede na u. Če je u=2πx/L, potem je x=-L/2 za u=-π in x=L/2 za u=π. Naj bo tudi f(x)=f(Lu/2π)=F(u). Fourierjeva vrsta F(u) ima obliko
Kje so koeficienti Fourierove vrste,
Vendar pogosteje zgornja formula povzroči odvisnost od x. Ker je u=2πx/L, to pomeni du=(2π/L)dx, meje integracije pa so od -L/2 do L/2 namesto od -π do π. Posledično ima Fourierjeva vrsta za odvisnost od x obliko
kjer so v območju od -L/2 do L/2 koeficienti Fourierjeve vrste,
(Meje integracije lahko nadomestimo s poljubnim intervalom dolžine L, na primer od 0 do L)
Fourierjeva vrsta na polciklu za funkcije, določene v intervalu L≠2π.
Za zamenjavo u=πх/L interval od x=0 do x=L ustreza intervalu od u=0 do u=π. Posledično lahko funkcijo razširimo v niz samo v kosinusih ali samo v sinusih, tj. V Fourierjeva vrsta na pol cikla.
Kosinusna ekspanzija v območju od 0 do L ima obliko
Fourierjeva vrsta periodičnih funkcij s periodo 2π.
Fourierjeva vrsta nam omogoča preučevanje periodičnih funkcij tako, da jih razgradimo na komponente. Izmenični tokovi in napetosti, pomiki, hitrosti in pospeški ročičnih mehanizmov ter akustični valovi so tipični praktični primeri uporabe periodičnih funkcij v inženirskih izračunih.
Razširitev v Fourierjev niz temelji na predpostavki, da je mogoče vse funkcije praktičnega pomena v intervalu -π ≤x≤ π izraziti v obliki konvergentnih trigonometričnih nizov (niz velja za konvergentnega, če je zaporedje delnih vsot, sestavljenih iz njegovih členov konvergira):
Standardni (=navadni) zapis skozi vsoto sinx in cosx
f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,
kjer so a o, a 1,a 2,...,b 1,b 2,.. realne konstante, tj.
Pri čemer so za območje od -π do π koeficienti Fourierjeve vrste izračunani po formulah:
Koeficienti a o , a n in b n se imenujejo Fourierjevi koeficienti, in če jih je mogoče najti, se pokliče serija (1). poleg Fourierja, ki ustreza funkciji f(x). Za niz (1) imenujemo člen (a 1 cosx+b 1 sinx) prvi oz osnovni harmonik,
Drug način za pisanje serije je uporaba relacije acosx+bsinx=csin(x+α)
f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)
Kjer je a o konstanta, c 1 =(a 1 2 +b 1 2) 1/2, c n =(a n 2 +b n 2) 1/2 so amplitude različnih komponent in je enako a n =arctg a n /b n.
Za vrsto (1) se člen (a 1 cosx+b 1 sinx) ali c 1 sin(x+α 1) imenuje prvi oz. osnovni harmonik,(a 2 cos2x+b 2 sin2x) ali c 2 sin(2x+α 2) se imenuje drugi harmonik in tako dalje.
Za natančno predstavitev kompleksnega signala je običajno potrebno neskončno število izrazov. Vendar je v mnogih praktičnih problemih dovolj, da upoštevamo samo prvih nekaj členov.
Fourierjeva vrsta neperiodičnih funkcij s periodo 2π.
Razširitev neperiodičnih funkcij.
Če je funkcija f(x) neperiodična, to pomeni, da je ni mogoče razširiti v Fourierjev niz za vse vrednosti x. Vendar pa je mogoče definirati Fourierjev niz, ki predstavlja funkcijo v poljubnem območju širine 2π.
Glede na neperiodično funkcijo je mogoče konstruirati novo funkcijo tako, da izberete vrednosti f(x) znotraj določenega območja in jih ponovite zunaj tega območja v intervalih 2π. Ker je nova funkcija periodična s periodo 2π, jo je mogoče razširiti v Fourierjev niz za vse vrednosti x. Na primer, funkcija f(x)=x ni periodična. Če pa jo je treba razširiti v Fourierjev niz v intervalu od o do 2π, se izven tega intervala sestavi periodična funkcija s periodo 2π (kot je prikazano na spodnji sliki).
Za neperiodične funkcije, kot je f(x)=x, je vsota Fourierjevega niza enaka vrednosti f(x) v vseh točkah v danem območju, vendar ni enaka f(x) za točke izven obsega. Za iskanje Fourierjeve vrste neperiodične funkcije v območju 2π se uporablja ista formula Fourierjevih koeficientov.
Sode in lihe funkcije.
Pravijo, da je funkcija y=f(x) celo, če je f(-x)=f(x) za vse vrednosti x. Grafi sodih funkcij so vedno simetrični glede na os y (to pomeni, da so zrcalne slike). Dva primera sodih funkcij: y=x2 in y=cosx.
Pravijo, da je funkcija y=f(x) čudno,če je f(-x)=-f(x) za vse vrednosti x. Grafi lihih funkcij so vedno simetrični glede na izvor.
Mnoge funkcije niso niti sode niti lihe.
Razširitev v Fourierjev niz v kosinuse.
Fourierjeva vrsta sode periodične funkcije f(x) s periodo 2π vsebuje samo kosinusne člene (tj. brez sinusnih členov) in lahko vključuje konstanten člen. torej
kje so koeficienti Fourierove vrste,
Fourierjeva vrsta lihe periodične funkcije f(x) s periodo 2π vsebuje samo člene s sinusi (to pomeni, da ne vsebuje členov s kosinusi).
torej
kje so koeficienti Fourierove vrste,
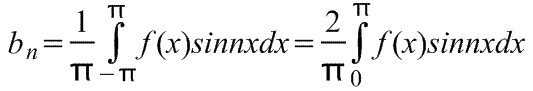
Fourierjeva vrsta na pol cikla.
Če je funkcija definirana za obseg, recimo od 0 do π, in ne samo od 0 do 2π, jo je mogoče razširiti v vrsto samo v sinusih ali samo v kosinusih. Nastala Fourierjeva vrsta se imenuje blizu Fourierja na pol cikla.
Če želite dobiti razgradnjo Fourierjev polciklični kosinus funkcije f(x) v območju od 0 do π, potem je treba zgraditi sodo periodično funkcijo. Na sl. Spodaj je funkcija f(x)=x, zgrajena na intervalu od x=0 do x=π. Ker je soda funkcija simetrična glede na os f(x), narišemo premico AB, kot je prikazano na sliki. spodaj. Če predpostavimo, da je zunaj obravnavanega intervala nastala trikotna oblika periodična s periodo 2π, potem končni graf izgleda takole: na sl. spodaj. Ker moramo kot prej pridobiti Fourierjevo razširitev v kosinusih, izračunamo Fourierjeva koeficienta a o in a n
Če morate dobiti Fourierjeva sinusna ekspanzija polcikla funkcije f(x) v območju od 0 do π, potem je treba zgraditi liho periodično funkcijo. Na sl. Spodaj je funkcija f(x)=x, zgrajena na intervalu od x=0 do x=π. Ker je liha funkcija simetrična glede na izvor, sestavimo premico CD, kot je prikazano na sl. Če predpostavimo, da je zunaj obravnavanega intervala nastali žagasti signal periodičen s periodo 2π, potem ima končni graf obliko, prikazano na sl. Ker moramo kot prej pridobiti Fourierjevo razširitev polcikla v smislu sinusov, izračunamo Fourierjev koeficient. b
Fourierjeva vrsta za poljuben interval.
Razširitev periodične funkcije s periodo L.
Periodična funkcija f(x) se ponavlja, ko x narašča za L, tj. f(x+L)=f(x). Prehod s predhodno obravnavanih funkcij s periodo 2π na funkcije s periodo L je dokaj preprost, saj ga lahko izvedemo s spremembo spremenljivke.
Za iskanje Fourierjeve vrste funkcije f(x) v območju -L/2≤x≤L/2 uvedemo novo spremenljivko u, tako da ima funkcija f(x) periodo 2π glede na u. Če je u=2πx/L, potem je x=-L/2 za u=-π in x=L/2 za u=π. Naj bo tudi f(x)=f(Lu/2π)=F(u). Fourierjeva vrsta F(u) ima obliko
(Meje integracije lahko nadomestimo s poljubnim intervalom dolžine L, na primer od 0 do L)
Fourierjeva vrsta na polciklu za funkcije, določene v intervalu L≠2π.
Za zamenjavo u=πх/L interval od x=0 do x=L ustreza intervalu od u=0 do u=π. Posledično lahko funkcijo razširimo v niz samo v kosinusih ali samo v sinusih, tj. V Fourierjeva vrsta na pol cikla.
Kosinusna ekspanzija v območju od 0 do L ima obliko
