Pickova formula

1. Uvod

2. Peakova formula. Razstava I.

Dokaz II.

Dokaz Š.

3. Cilji.

4. Formula za območje poligona z uporabo koordinat oglišč.

5. Naloge.

6. Literatura

Peakova formula.

1. Uvod.

Iz zgodovine črpamo modrost,

v poeziji - duhovitost,

pri matematiki - vpogled.

F. Bacon

Zaplet se bo odvijal na navadnem kosu karirastega papirja.

Črte, ki potekajo ob straneh celic, tvorijo mrežo, vrhovi celic pa so vozlišča te mreže. Na list narišimo mnogokotnik z oglišči v vozliščih in poiščimo njegovo ploščino.

Iščete ga lahko na različne načine. Na primer, mnogokotnik lahko razrežete na dokaj preproste oblike, poiščete njihova območja in jih seštejete.

Toda tukaj nas čaka veliko težav. Lik zlahka razdelimo na pravokotnike, trapeze in trikotnike, njegovo površino pa izračunamo brez napora.

Čeprav je mnogokotnik videti dovolj preprost, je za izračun njegove površine potrebno veliko dela. Kaj pa, če bi poligon izgledal bolj elegantno? Izkazalo se je, da je mogoče površine poligonov, katerih oglišča se nahajajo na vozliščih mreže, izračunati veliko preprosteje: obstaja formula, ki njihovo površino poveže s številom vozlišč, ki ležijo znotraj in na meji poligona. Ta čudovita in preprosta formula se imenuje Pick formula.

2. Peakova formula.

Oglišča mnogokotnika (ni nujno konveksnega) se nahajajo na vozliščih celoštevilske mreže. V njem leži B vozlišča mreže, na meji pa G vozlišča. Dokažimo, da je njegova ploščina enaka B + – 1 (Izberi formulo).

Razstava I.

Razmislimo o mnogokotniku, katerega oglišča se nahajajo na vozliščih celoštevilske mreže, to pomeni, da imajo cele koordinate.

Mnogokotnik razdelimo na trikotnike z oglišči v vozliščih mreže, ki ne vsebujejo nobenih vozlišč niti znotraj niti ob straneh.

Označimo:

n– število stranic mnogokotnika,

m– število trikotnikov z oglišči v vozliščih mreže, ki ne vsebujejo vozlišč niti znotraj niti ob straneh,

B – število vozlišč znotraj poligona,

Г – število vozlišč na straneh, vključno z oglišči.

Ploščine vseh teh trikotnikov so enake in enake.

Zato je območje poligona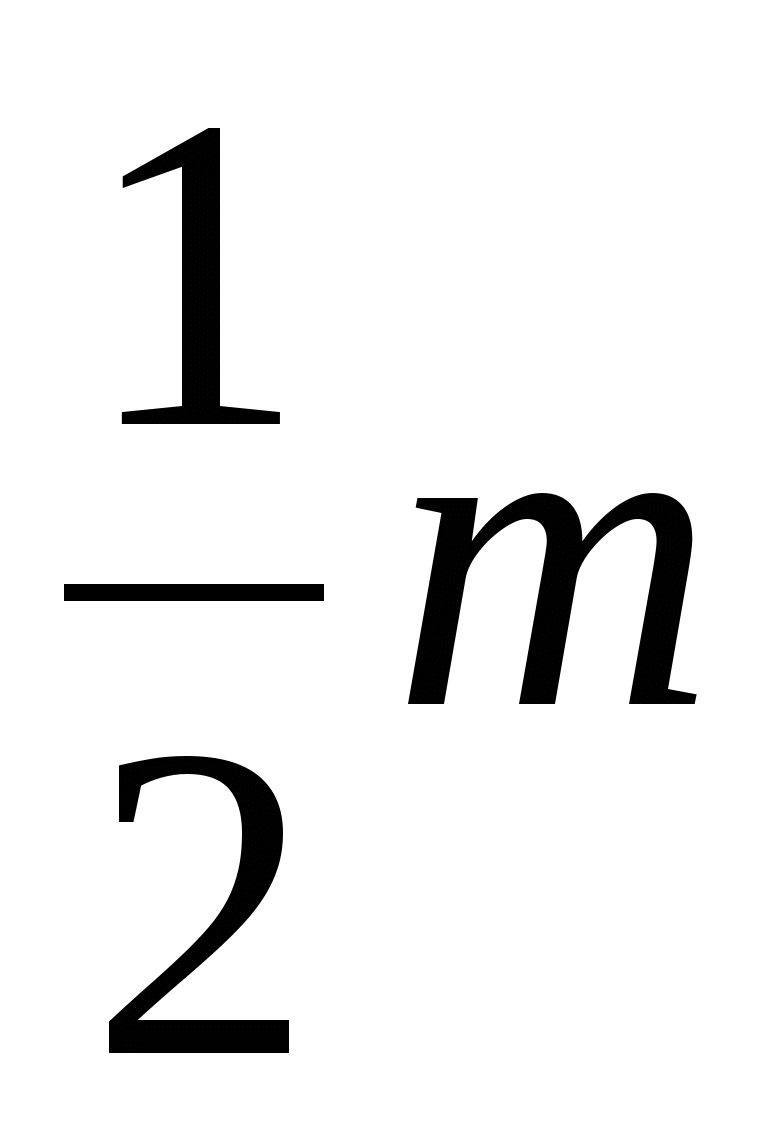
.

180 0 m .

Zdaj pa poiščimo ta znesek na drug način.

Vsota kotov z vrhom v katerem koli notranjem vozlišču je 360 ​​0.

Potem je vsota kotov z oglišči na vseh notranjih vozliščih enaka 360 0 V.

Skupna vsota kotov za vozlišča na straneh, vendar ne na ogliščih, je 180 0 (G - n).

Vsota kotov na ogliščih mnogokotnika je 180 0 ( n – 2) .

Skupna vsota kotov vseh trikotnikov je 360 0 V + 180 0 (G – n) + 180 0 (n – 2).

Torej 1800 m= 360 0 V + 180 0 (G – n) + 180 0 (n – 2),

180 0 m= 360 0 V + 180 0 G – 180 0 n + 180 0 n– 180 0 2,

180 0 m= 360 0 V + 180 0 G – 360 0,

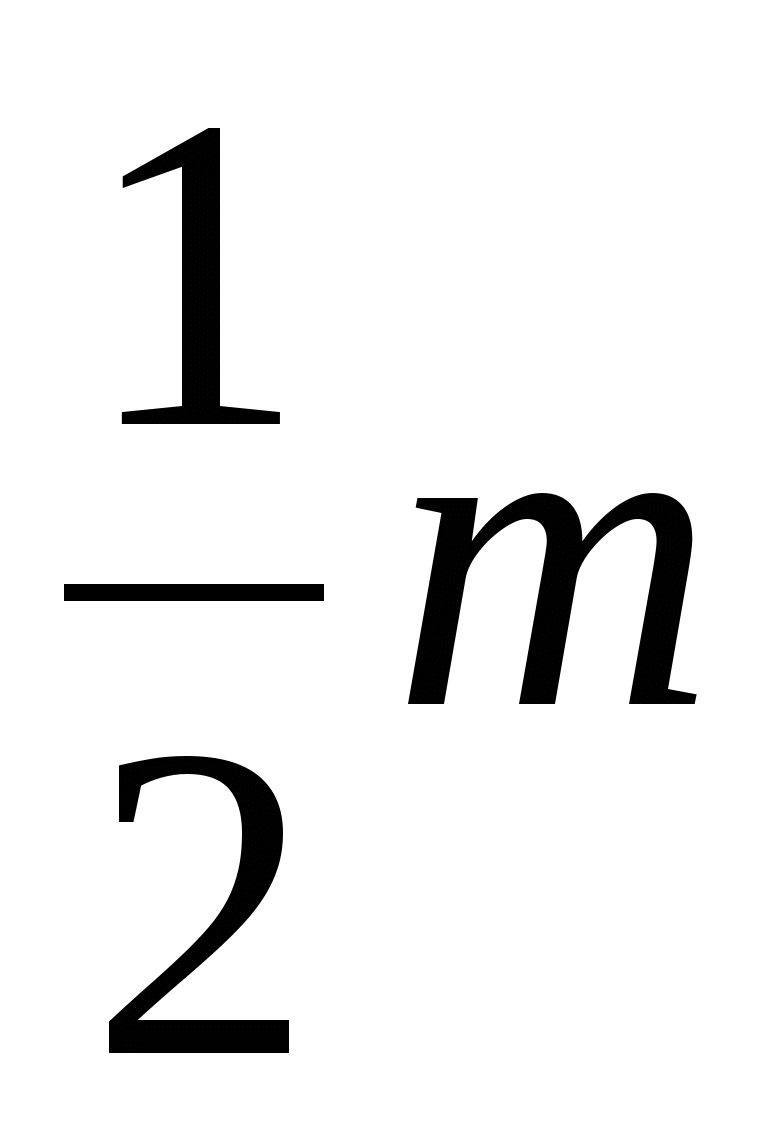= B + – 1 ,

iz katerega dobimo izraz za ploščino S mnogokotnika:

S= B + – 1 ,

znana kot Pickova formula.

Na sliki: B = 24, D = 9, torejS = 24 + – 1 = 27,5.

Poiščimo površino prvega poligona z uporabo Peakove formule:

B = 28 (zelene pike);

G = 20 (modre pike).

Dobimo, S =
= 37 kvadratnih enot

Dokaz II.

Vsakemu poligonu M z oglišči v vozliščih celoštevilske mreže priredimo število f (M) =
, kjer se seštevek izvede po vseh vozliščih mreže, ki pripadajo M, in kotu je opredeljeno kot sledi: =
za notranjo točko poligona, =
za mejno točko, ki ni oglišče, in – oglišče, če je to vozlišče oglišče. Lahko vidimo, da je f(M) =
+
= B + – 1. Ostaja še preveriti, ali je število f (M) enako površini poligona M.

Naj bo mnogokotnik M razrezan na poligona M 1 in M ​​2 z oglišči v vozliščih mreže. Potem je f (M) = f (M 1) + f (M 2), saj se za vsako vozlišče seštejejo koti. Če torej Pickova formula velja za dva poligona M, M 1 in M ​​2, potem velja tudi za tretjega.

Če je M pravokotnik s stranicami str in q, usmerjen vzdolž mrežnih črt, torej

f (M) = (p – 1)(q – 1) +
= pq.

V tem primeru velja Peakova formula. Če razrežemo pravokotnik M z diagonalo na trikotnika M 1 in M ​​2 in uporabimo dejstvo, da je f (M) = f (M 1) + f (M 2) in f (M 1) = f (M 2), je je enostavno dokazati veljavnost Pickove formule za kateri koli pravokotni trikotnik s kraki, usmerjenimi vzdolž mrežnih črt. Če izrežete več teh trikotnikov iz pravokotnika, lahko dobite poljuben trikotnik.

Za dokončanje dokaza Pickove formule je treba ugotoviti, da je vsak mnogokotnik mogoče razrezati na trikotnike z ločenimi diagonalami.

Dokaz Š.

Razmerje med površino figure in številom vozlišč, vključenih v to sliko, je še posebej jasno vidno v primeru pravokotnika.

Naj ABCD- pravokotnik z oglišči na vozliščih in stranicah, ki potekajo vzdolž mrežnih črt.

Označimo z INštevilo vozlišč, ki ležijo znotraj pravokotnika, in skozi G- število vozlišč na njegovi meji. Premaknimo mrežo za pol celice v desno in za pol celice navzdol.

Nato lahko ozemlje pravokotnika "razporedimo" med vozlišča na naslednji način: vsako od IN vozlišča »nadzirajo« celotno celico premaknjene mreže, vsako od G– 4 obrobna nekotalna vozlišča so polovica celice, vsaka kotna točka pa je četrtina celice. Zato je površina pravokotnika S enaka

Torej smo za pravokotnike z oglišči na vozliščih in stranicah vzdolž mrežnih črt določili formulo

Dokažimo, da ta formula ne velja samo za pravokotnike, ampak tudi za poljubne poligone z oglišči v vozliščih mreže.

Označimo z S m območje poligonaM z oglišči v vozliščih in skozip m – velikost
, KjeIN m – število vozlišč v notranjostiM, A G m - število vozlišč na meji. Potem lahko Peakovo formulo zapišemo kot
.

Dokaz formule bomo razdelili na več korakov.

1. korak

Če poligonM z oglišči v vozliščih mreže, razrezanih na 2 poligonaM 1 in M 2 , potem ima tudi vozlišča le v vozliščih mreže
. Naj poligonM razrezane na poligoneM 1 in M 2 z oglišči v vozliščih z segmentom AB. Vsa vozlišča, razen tistih, ki spadajo na segmentAB, enako prispevajo k levi in ​​desni strani formule. Oglejmo si vozlišča, ki ležijo na segmentu AB.

Če takšno vozlišče leži med A in B (na primer C), potem za mnogokotnikM je notranji in za mnogokotnikeM 1 in M 2 – mejni. Zato je njegov prispevek kp m je enako 1 in v vsakem od izrazov
in
– 0,5 vsak, torej prispevki takega vozlišča kp m in
so enaki.

Oglejmo si vozlišči A in B. Sta mejni vozlišči za oba M, in za M 1 , M 2 .

Zato je prispevek vsakega od teh vozlišč kp m enako 0,5 a in
- enota. To pomeni, da skupni prispevek vozlišč A in B kp m je enako 1, kar je 1 manj od njihovega prispevka k
. Ampak
, A .

Od skupnega "prispevka" vseh vozlišč p m 1 se odšteje in od
2 se odšteje in to kompenzira razliko v prispevkih vozlišč A in B.

Torej,
.

2. korak

Če poligon M z oglišči v vozliščih mreže, razrezanih na dva poligona M 1 in M 2 (tudi z vozlišči v vozliščih) in formula je pravilna za nekatera dva mnogokotnika MM 1 , M 2 , potem velja tudi za tretji poligon.

Naj na primer velja zaM 1 in M 2 , to je
. Nato (s prvim korakom), ampak (z prvi korak) je zadnji izraz enakp m , in enakost
in obstaja formula Peak.

3. korak

Dokažimo Peakovo formulo za pravokotni trikotnik z oglišči v vozliščih mreže in kraki, ki ležijo na mrežnih črtah.

Trikotnik ABC zgradite ga v pravokotnik ABCD .

Za pravokotnike je Pickova formula pravilna: S ABCD = P ABCD . Glede na prvi korak p ABCD = P ABC + P ACD , P ABC = P ACD , torej p ABCD = 2P ABC . Ampak S ABCD = 2 S ABC . zato S ABC = P ABC .

4. korak

Pickova formula velja za poljuben trikotnik z oglišči v vozliščih mreže.

Po pregledu slike je enostavno razumeti: vsak tak trikotnik lahko dobite tako, da "odrežete" iz določenega pravokotnika s stranicami vzdolž mrežnih črt, več pravokotnikov in pravokotnih trikotnikov s kraki na mrežnih črtah. In ker Peakova formula velja za pravokotnike in pravokotne trikotnike, potem (zapomnite si korak 2) velja tudi za prvotni trikotnik.

Dokazali smo, da če je mnogokotnik mogoče razrezati na trikotnike z oglišči v vozliščih mreže, potem zanj velja Peakova formula.

3. Cilji.

Poiščite površino figur:

1
.

B=9

G = 4

B=9

G = 5

Mnogokotnik brez samopresečišč se imenuje mreža, če se vsa njegova oglišča nahajajo v točkah s celimi koordinatami (v kartezičnem koordinatnem sistemu).

Pickov izrek

Formula

Naj nam bo dan nek mrežni poligon z neničelno ploščino.

Označimo njegovo območje z ; število točk s celimi koordinatami, ki ležijo strogo znotraj mnogokotnika; število točk s celimi koordinatami, ki ležijo na stranicah mnogokotnika - skozi .

Nato se je poklicala relacija Pickova formula:

Zlasti, če sta vrednosti I in B znani za določen mnogokotnik, se lahko njegova površina izračuna kot , tudi brez poznavanja koordinat njegovih vrhov.

To razmerje je leta 1899 odkril in dokazal avstrijski matematik Georg Alexander Pick.

Dokaz

Dokaz poteka v več fazah: od najpreprostejših likov do poljubnih poligonov:

Posploševanje na višje dimenzije

Na žalost se ta preprosta in lepa Peakova formula ne posplošuje dobro na višje dimenzije.

To je jasno pokazal Reeve, ki je leta 1957 predlagal, da se upošteva tetraeder (danes imenovan Reeve tetraeder) z naslednjimi vozlišči:

kje je poljubno naravno število. Potem ta tetraeder za nobeno ne vsebuje niti ene točke s celimi koordinatami v notranjosti in na njegovi meji so samo štiri točke , , , in nobena druga. Tako sta prostornina in površina tega tetraedra lahko drugačna, medtem ko je število točk znotraj in na meji nespremenjeno; zato Pickova formula ne dopušča posploševanja niti na tridimenzionalni primer.

Kljub temu še vedno obstaja nekaj podobnega posploševanja na prostore višjih dimenzij – to Ehrhartovi polinomi(Ehrhartov polinom), vendar so zelo zapleteni in niso odvisni samo od števila točk znotraj in od roba figure.

Za oceno površine poligona na karirastem papirju je dovolj, da preštejemo, koliko celic ta poligon pokriva (površino celice vzamemo kot eno). Natančneje, če S- ploščino mnogokotnika, - število celic, ki v celoti ležijo znotraj mnogokotnika, in - število celic, ki imajo vsaj eno skupno točko z notranjostjo mnogokotnika.

V nadaljevanju bomo obravnavali samo takšne poligone, katerih vsa oglišča ležijo v vozliščih karirastega papirja - v tistih, kjer se mrežne črte sekajo. Izkazalo se je, da lahko za takšne poligone podamo naslednjo formulo:

kje je območje, r- število vozlišč, ki ležijo strogo znotraj poligona.

Ta formula se imenuje "Pick formula" - po matematiku, ki jo je odkril leta 1899.

Preprosti trikotniki

Ploščino katerega koli trikotnika, narisanega na karirastem papirju, lahko enostavno izračunate tako, da jo predstavite kot vsoto ali razliko ploščin pravokotnih trikotnikov in pravokotnikov, katerih stranice sledijo mrežnim črtam, ki potekajo skozi oglišča narisanega trikotnika. Ko to storite na primer za trikotnike, prikazane na sliki 1.34, se lahko prepričate, da je površina vedno enaka "prejetemu" številu - številu oblike, kjer je celo število.

Imenujmo trikotnik preprost, če v njem ali na njegovih straneh ni mrežnih vozlišč, razen njegovih oglišč. Vsi preprosti trikotniki na sl. 1,34 imajo površino. Videli bomo, da to ni naključje.

Naloga. Tri kobilice (tri točke) v začetnem trenutku sedijo na treh ogliščih ene celice, nato pa začnejo "igrati skakalnico": vsaka lahko preskoči enega od drugih dveh, nato pa konča na točki, ki je simetrična relativno svojemu (sl. 1.35, jasno, da bodo kobilice po poljubnem številu takih skokov padle v vozle karirastega papirja). V kateri trojki točk se lahko znajdejo kobilice po nekaj skokih?

Trikotnik imenujemo dosegljiv, če se lahko na njegovih ogliščih hkrati pojavijo tri kobilice, ki so bile sprva na treh ogliščih ene celice; preskok bomo imenovali transformacija trikotnika, ki je sestavljena iz dejstva, da gre eno od oglišč v točko, ki je simetrična glede na katero koli od drugih dveh oglišč (ti dve oglišči ostaneta na mestu).

1. izrek. Naslednje tri lastnosti trikotnikov z oglišči na vozliščih karirastega papirja so med seboj enakovredne:

1) trikotnik ima ploščino,

2) trikotnik je preprost,

3) trikotnik je dosegljiv.

Spoznajmo naslednje lastnosti preprostega trikotnika, ki vodijo do veljavnosti tega izreka.

1. Območje trikotnika se pri skakanju ne spremeni.

2. Vsak dosegljiv trikotnik ima ploščino.

3. Če dokončate preprost trikotnik ABC na paralelogram ABCD, potem ne bo nobenih vozlišč (brez štetja oglišč) ne znotraj ne na straneh tega paralelograma.

4. Iz preprostega trikotnika pri skakanju dobimo preprost trikotnik.

5. Iz preprostega trikotnika je eden od kotov tup ali raven (in slednji primer je možen le za trikotnik, katerega tri oglišča pripadajo eni celici; tak preprost trikotnik s stranicami 1, 1 se bo imenoval minimalen.)

6. Iz katerega koli enostavnega neminimalnega trikotnika lahko z enim skokom dobimo trikotnik, katerega najdaljša stranica je manjša od najdaljše stranice prvotne.

7. Vsak preprost trikotnik je mogoče pretvoriti v minimalnega s končnim številom skokov.

8. Vsak preprost trikotnik je dosegljiv.

9. Vsak preprost trikotnik ima ploščino.

10. Vsak trikotnik lahko razrežemo na preproste.

11. Površina katerega koli trikotnika je enaka in vsakič, ko je razrezan na praštevila, je njihovo število enako m.

12. Vsak trikotnik ploščine je preprost.

13. Za katerikoli dve vozlišči A in IN rešetke, na segmentu, med katerima ni drugih vozlišč, je vozlišče Z tako, da trikotnik ABC- preprosto.

14. Vozel Z v prejšnji lastnosti lahko vedno izberete tako, da kot DIA bo topo ali ravno.

15. Naj bo karirasta ravnina razrezana na enake paralelograme, tako da so vsa vozlišča oglišča paralelogramov. Potem je vsak od trikotnikov, v katerega je eden od teh paralelogramov razrezan s svojo diagonalo, preprost.

16. (Hratna stran 15). Trikotnik ABC- preprosta, če in samo, če so vsi možni trikotniki pridobljeni iz ABC vzporedni prevodi, ki prenašajo vozlišče A v različna vozlišča mreže, se med seboj ne prekrivajo.

17. Če je mreža - vozlišča karirastega papirja - razdeljena na štiri podmreže s celicami (slika 1.36), bodo oglišča preprostega trikotnika nujno padla v tri različne podmreže (vse tri imajo različne oznake).

Naslednji dve lastnosti ponujata odgovor na problem treh kobilic.

18. Tri kobilice lahko hkrati zadenejo tiste in samo tiste trojke točk, ki služijo kot oglišča preprostega trikotnika in imajo enak predznak kot ustrezna oglišča začetnega trikotnika.

19. Dve kobilici lahko hkrati zadeneta tiste in samo tiste pare vozlišč ustreznih znakov, na segmentu, med katerima ni drugih vozlišč.

Poligonska triangulacija

Upoštevali bomo določeno vrsto poligonov na karirastem papirju, ki ustrezajo vrednostim v formuli Pick. Toda od tega posebnega primera lahko preidete naravnost do najsplošnejšega, z uporabo izreka o razrezu poljubnega mnogokotnika na trikotnike (karirasti papir ni več potreben).

Naj sta na ravnini podana mnogokotnik in neka končna množica TO točke, ki ležijo znotraj mnogokotnika in na njegovi meji (in vsa oglišča mnogokotnika pripadajo množici TO).

Triangulacija z oglišči TO imenujemo razdelitev danega mnogokotnika na trikotnike z oglišči v množici TO tako, da vsaka točka od TO služi kot vrh vsakega od tistih triangulacijskih trikotnikov, ki jim ta točka pripada (to so točke iz TO ne padejo v notranjost ali na stranice trikotnikov, sl. 1.37).

2. izrek. a) Kateri koli n-trikotnik lahko diagonalno razrežemo na trikotnike in število trikotnikov bo enako n- 2 (ta particija je triangulacija z oglišči na ogliščih n-gon).

b) Označena naj bo meja mnogokotnika r točke (vključno z vsemi vozlišči), znotraj - več i točke. Nato je triangulacija z oglišči na označenih točkah, število trikotnikov takšne triangulacije pa bo enako.

Seveda je a) poseben primer b), ko.

Veljavnost tega izreka izhaja iz naslednjih trditev.

1) Iz vrha največjega kota n-gon () vedno je mogoče narisati diagonalo, ki v celoti leži znotraj poligona.

2) Če n-kvadrat je diagonalno razrezan na r- kvadrat in q-gon, torej.

3) Vsota kotov n-gon je enak.

4) Kateri koli n-trikotnik lahko diagonalno razrežemo na trikotnike.

5) Za vsak trikotnik, znotraj in na meji katerega je označenih več točk (vključno z vsemi tremi njegovimi oglišči), obstaja triangulacija z oglišči na označenih točkah.

6) Enako velja za vsakogar n-gon.

7) Število triangulacijskih trikotnikov je enako, kjer je i in r- število označenih več točk znotraj in na meji poligona. Pokličimo particijo n-kotnik v več mnogokotnikov je pravilen, če vsako oglišče enega od poligonov particije služi kot oglišče vseh drugih mnogokotnikov particije, ki ji pripada. 8) Če iz oglišč k-gonov, na katere so razdeljeni na pravilen način n-gon, i oglišča ležijo znotraj in r- na meji n-gon, potem pa količina k-goni so enaki

9) Če točke ravnine in segmenti s konci na teh točkah tvorijo mnogokotnik, pravilno razdeljen na mnogokotnike, potem (slika 1.38)

Iz izrekov 1 in 2 sledi formula Peak:

1.5 Pitagorov izrek o vsoti ploščin kvadratov, zgrajenih na stranicah pravokotnega trikotnika

Izrek. Vsota površin kvadratov, zgrajenih na straneh pravokotnega trikotnika, je enaka površini kvadrata, zgrajenega na hipotenuzi tega trikotnika. Naj ABC(slika 1.39) je pravokoten trikotnik in BDEA, AFGE in BCKH- kvadrati, zgrajeni na njegovih katetah in hipotenuzi; morate dokazati, da je vsota površin prvih dveh kvadratov enaka površini tretjega kvadrata.

Izvajajmo sonce. Nato kvadrat BCKH bo razdeljen na dva pravokotnika. Dokažimo, da pravokotnik BLMH enaka kvadratu BDEA, in pravokotnik LCKM enaka kvadratu AFGC.

Narišimo pomožne črte DC in AN. Razmislite o trikotnikih DCB in ABH. Trikotnik DCB imeti osnovo BD, skupno s kvadratom BDEA, in višino CN, enako višini AB tega kvadrata je enako polovici kvadrata. Trikotnik AVN imeti osnovo VN, skupno s pravokotnikom BLMH, in višino AR, enako višini B.L. tega pravokotnika, enaka njegovi polovici. Če ta dva trikotnika primerjamo med seboj, ugotovimo, da imata BD = VA in BC = VN(kot stranice kvadrata);

Še več, DCB = AVN, saj je vsak od teh kotov sestavljen iz skupnega dela - ABC in pravim kotom. Torej trikotniki AVN in BCD so enaki. Iz tega sledi, da pravokotnik BLMN enaka kvadratu BDEA. Na enak način je dokazano, da je pravokotnik LGKM enaka kvadratu AFGC. Iz tega sledi, da kvadrat VSKN enaka vsoti kvadratov BDEA in AFGC.

Izračun površine figure.

Način izbire

Delo učenca 5B razreda srednje šole MBOU št. 23 v Irkutsku

Balsukova Aleksandra

Vodja: Khodyreva T.G.

2014

Izračun površine figure. Način izbire

Predmet študija : naloge na karo papirju

Predmet raziskave : težave za izračun površine poligona na karirastem papirju, metode in tehnike za njihovo reševanje.

Raziskovalne metode : primerjava, posploševanje, analogije, študij literature in internetnih virov, analiza informacij.

Namen študije:

izberite glavne, zanimive, razumljive informacije

Analizirajte in sistematizirajte prejete informacije

Poiščite različne metode in tehnike za reševanje problemov na karirastem papirju

preverite formule za izračun ploščin geometrijskih likov s formulo Pick

Izdelati elektronsko predstavitev dela za predstavitev zbranega gradiva

Geometrija je najmočnejše sredstvo za izostritev naših mentalnih sposobnosti in nam omogoča pravilno razmišljanje in sklepanje.

(G. Galileo)

Relevantnost teme

Strast do matematike se pogosto začne z razmišljanjem o problemu. Torej, pri preučevanju teme "Območje poligonov" se postavlja vprašanje, ali obstajajo težave, ki se razlikujejo od težav, obravnavanih v učbeniku. Takšne težave vključujejo težave na karirastem papirju. Kakšna je posebnost takih problemov, ali obstajajo posebne metode in tehnike za reševanje problemov na karirastem papirju. Pri uri matematike nam je učiteljica predstavila zanimivo metodo računanja mnogokotnikov. Začel sem preučevati literaturo in internetne vire na to temo. Zdi se, da je na karirasti ravnini, torej na neskončnem listu papirja, nanizanem v enake kvadratke, mogoče najti nekaj zanimivega. Izkazalo se je, da so opravila, povezana s karirastim papirjem, precej raznolika. Naučil sem se izračunati ploščino poligonov, narisanih na karirasti list papirja. Za veliko problemov na kvadratnem papirju ni splošnega pravila za reševanje ali posebnih metod in tehnik. To je njihova lastnost, ki določa njihovo vrednost za razvoj ne posebne akademske sposobnosti ali veščine, ampak na splošno sposobnosti razmišljanja, refleksije, analize, iskanja analogij, torej te naloge razvijajo miselne sposobnosti v njihovem najširšem pomenu.

Izvedel sem tudi, da so takšne naloge upoštevane v testnih in merilnih gradivih Državne akademije znanosti in Enotnega državnega izpita. Zato menim, da je preučevanje tega gradiva koristno za njegovo uporabo ne le v nadaljnjem izobraževalnem procesu, temveč tudi za reševanje nestandardnih olimpijadnih problemov.

2.Koncept območja

kvadrat- numerična značilnost dvodimenzionalne geometrijske figure, ki prikazuje velikost te figure. Zgodovinsko se je izračun površine imenoval . Slika, ki ima ploščino, se imenuje na kvadrat .

Območje ravne figure glede na geometrijo

1. kvadrat-mera ravninske figure glede na standardno figuro, ki je kvadrat s stranico, enako eni dolžinski enoti.

2. kvadrat- numerična značilnost, pripisana ravnim figuram določenega razreda (na primer poligoni). Površina kvadrata s stranico, ki je enaka enoti dolžine, velja za enako enoti površine

3. kvadrat- pozitivna količina, katere številčna vrednost ima naslednje lastnosti:

 Enake figure imajo enake površine;

 Če je figura razdeljena na dele, ki so preproste figure (to je tiste, ki jih je mogoče razdeliti na končno število ravninskih trikotnikov), potem je površina te figure enaka vsoti površin njenih delov;

 Površina kvadrata s stranico, enako eni merski enoti, je enaka ena.

Tako lahko sklepamo, da območje ni določena količina, ampak daje le neko pogojno značilnost katere koli ploščate figure. Če želite najti območje poljubne figure, morate ugotoviti, koliko kvadratov s stranico, ki je enaka enoti dolžine, vsebuje. Na primer, vzemite pravokotnik, v katerem se kvadratni centimeter prilega natanko 6-krat. To pomeni, da je površina pravokotnika 6 cm 2.

Izbira površine kvadrata s stranico, enako merski enoti, kot najmanjše merske enote vseh površin ni naključna. To je rezultat dogovora med ljudmi, ki je nastal v teku "naravne" stoletne selekcije. Poleg tega so bili še drugi predlogi za mersko enoto. Tako je bilo na primer predlagano, da se kot taka enota vzame območje enakostraničnega trikotnika (tj. Vsaka ravna figura bi lahko bila predstavljena kot "vsota" določenega števila enakostraničnih trikotnikov), kar bi vodilo do sprememba številčne zastopanosti površin.

Tako so se formule za izračun površin pojavile v matematiki in jih človek ni takoj spoznal - to veliko znanstvenikov, ki živijo v različnih obdobjih in različnih državah. (Nepravilne formule niso našle mesta v znanosti in so izginile v pozabo). Prave formule so se skozi tisočletja dopolnjevale, popravljale in utemeljevale, dokler niso prišle do nas v moderni preobleki.

ista stvar merjenje površine je sestavljen iz primerjave površine dane figure s površino figure, ki je vzeta kot merska enota. Kot rezultat primerjave dobimo določeno število - številčno vrednost površine dane figure. Ta številka kaže, kolikokrat je površina določene figure večja (ali manjša) od površine figure, ki je vzeta kot enota za merjenje površine.

T Tako lahko sklepamo, da je ploščina umetna količina, ki jo je človek zgodovinsko uvedel za merjenje neke lastnosti ploščate figure. Potrebo po vnosu takšne vrednosti je določila naraščajoča potreba po tem, kako veliko je določeno ozemlje, koliko žita je potrebno za posejanje njive ali izračun talne površine za okrasitev okrasnih ploščic.

Pickova formula

Za oceno površine poligona na karirastem papirju je dovolj, da preštejemo, koliko celic ta poligon pokriva (površino celice vzamemo kot eno). Natančneje, čeS je površina poligona, B je število celic, ki v celoti ležijo znotraj poligona, G pa število celic, ki imajo notranjost. Upoštevali bomo samo take poligone, katerih vsa oglišča ležijo v vozliščih karirastega papirja - tiste, kjer mrežne črte poligonov sekajo vsaj eno skupno točko.

Ploščino katerega koli trikotnika, narisanega na karirastem papirju, lahko enostavno izračunate tako, da jo predstavite kot vsoto ali razliko ploščin pravokotnih trikotnikov in pravokotnikov, katerih stranice sledijo mrežnim črtam, ki potekajo skozi oglišča narisanega trikotnika.

Za izračun površine takšnega poligona lahko uporabite naslednji izrek:

Izrek . Naj - število celih točk znotraj poligona, - število celih točk na njegovi meji, - njegovo območje. Potem je poštenoPickova formula:

Primer. Za mnogokotnik na slikiL = 7 (rdeče pike), 9 (zelene pike) torejS = 7+ 9/2 -1 = 10,5 kvadratnih enot.

Pickov izrek- klasičen rezultat in .

Območje trikotnika z oglišči na vozliščih in brez vozlišč niti znotraj niti na straneh (razen oglišč) je 1/2. To dejstvo.

3. Zgodovina

Pickovo formulo je odkril avstrijski matematik Georg Alexander (1859-1942) l. . Pri 16 letih je Georg končal šolo in vstopil v. Pri 20 letih je dobil pravico poučevati fiziko in matematiko. Leta 1884 je Peake odšel v Za . Tam je srečal še enega od Kleinovih študentov,. Pozneje, leta 1885, se je vrnil v, kjer je preživel preostanek svoje znanstvene kariere.

Georg Pieck je bil prijatelj z Einsteinom. Peake in Einstein nista imela le skupnih znanstvenih interesov, ampak sta imela tudi strast do glasbe. Pick, ki je igral v kvartetu, sestavljenem iz univerzitetnih profesorjev, je Einsteina predstavil znanstvenim in glasbenim družbam v Pragi.

Paleta Peakeovih matematičnih zanimanj je bila izjemno široka. Predvsem imajo več kot 50 znanstvenih člankov. Pickov izrek za izračun površine poligona, ki ga je odkril leta 1899, je postal splošno znan. V Nemčiji je ta izrek vključen v šolske učbenike.

4.Uporaba formule Pick

Pickova formula se uporablja ne samo za izračun površin poligonov, temveč tudi za reševanje številnih problemov na ravni olimpijade.

Nekaj ​​primerov uporabe formule Pick pri reševanju nalog:

1) Šahovski kralj je hodil po plošči z 8 × 8 celicami in vsako obiskal

hišno polje natanko enkrat in z zadnjo potezo vrnitev na izvirnik

polje. Prekinjena črta, ki zaporedno povezuje središča polj, ki

prešel kralja, nima samopresečišč. Kakšno območje lahko

omejiti to prekinjeno črto? (Stran celice je 1.)

Iz Peakove formule takoj sledi, da je območje, omejeno z lo-

mana, enaka 64/2 − 1 = 31; tukaj so vozlišča mreže središča 64

polja in po pogoju vsa ležijo na meji poligona. torej

Torej, čeprav je takšnih kraljevih "trajektorij" precej, so vse

vezani poligoni enakih ploščin.

Naloge iz testnih in merilnih gradiv Državne izpitne agencije in Enotnega državnega izpita

Naloga B3

Poiščite površino figure, upodobljene na karirastem papirju z velikostjo celice 1 cm 1 cm (glej sliko). Odgovor zapišite v kvadratnih centimetrih.

4. Zaključek

Med raziskovalnim procesom sem preučevala referenčno in poljudnoznanstveno literaturo. Izvedel sem, da je problem iskanja ploščine mnogokotnika z oglišči na vozliščih mreže spodbudil avstrijskega matematika Piecka, da je leta 1899 dokazal izjemno Pieckovo formulo.

S svojim delom sem razširil svoje znanje o reševanju problemov na karirastem papirju, sam določil klasifikacijo obravnavanih problemov in se prepričal o njihovi raznolikosti.

Naučila sem se izračunati ploščine mnogokotnikov, narisanih na karirasti list papirja, ki imajo različne težavnostne stopnje - od enostavnih do olimpijskih. Vsakdo lahko med njimi najde naloge izvedljive stopnje zahtevnosti, od katerih bo mogoče preiti na reševanje težjih.

Ugotovil sem, da je tema, ki me zanima, precej večplastna, problemi na karirastem papirju so raznoliki, različne pa tudi metode in tehnike njihovega reševanja. Zato smo se odločili, da nadaljujemo delo v tej smeri.

5. Uporabljena literatura:

1. Vasiljev N. B. Okoli formule Pick // Quantum. - 1974. - Št. 12

2. K o k e P r a s o l o v V. V. Problemi v planimetriji. - M.: MTsNMO, 2006.t e r G.S.M. Uvod v geometrijo. - M.: Znanost, 1966

3. Roslova L.O., Sharygin I.F. Meritve. – M.: Založba. "Odprti svet", 2005.

Internetni viri:

:

Povratne informacije za delo

»Izračun površin ravninskih likov. Izberi metodo"

Upoštevanje te teme bo povečalo kognitivno aktivnost študenta, ki bo pozneje začel videti harmonijo risbe pri pouku geometrije in ne bo več dojemal geometrije (in matematike na splošno) kot dolgočasne znanosti.

Pregledala učiteljica matematike

Khodyreva Tatyana Georgievna