Układy równań liniowych. Rozwiązywanie układów równań liniowych metodą Gaussa

Rozwiązywanie układów liniowych równań algebraicznych (SLAE) jest niewątpliwie najważniejszym tematem zajęć z algebry liniowej. Ogromna liczba problemów ze wszystkich działów matematyki sprowadza się do rozwiązywania układów równań liniowych. Czynniki te wyjaśniają powód powstania tego artykułu. Materiał artykułu jest tak dobrany i skonstruowany, abyś przy jego pomocy mógł to zrobić

• wybrać optymalną metodę rozwiązania swojego układu liniowych równań algebraicznych,
• przestudiować teorię wybranej metody,
• rozwiązuj swój układ równań liniowych, rozważając szczegółowe rozwiązania typowych przykładów i problemów.

Krótki opis materiału artykułu.

Najpierw podajemy wszystkie niezbędne definicje, pojęcia i wprowadzamy oznaczenia.

Następnie rozważymy metody rozwiązywania układów liniowych równań algebraicznych, w których liczba równań jest równa liczbie nieznanych zmiennych i które mają jednoznaczne rozwiązanie. Po pierwsze skupimy się na metodzie Cramera, po drugie pokażemy macierzową metodę rozwiązywania takich układów równań, a po trzecie przeanalizujemy metodę Gaussa (metodę sekwencyjnej eliminacji nieznanych zmiennych). Aby utrwalić teorię, na pewno rozwiążemy kilka SLAE na różne sposoby.

Następnie przejdziemy do rozwiązywania układów liniowych równań algebraicznych o postaci ogólnej, w których liczba równań nie pokrywa się z liczbą nieznanych zmiennych lub główna macierz układu jest pojedyncza. Sformułujmy twierdzenie Kroneckera-Capelliego, które pozwala nam ustalić zgodność SLAE. Przeanalizujmy rozwiązanie układów (o ile są kompatybilne) wykorzystując pojęcie molowej podstawy macierzy. Rozważymy również metodę Gaussa i szczegółowo opiszemy rozwiązania przykładów.

Na pewno zatrzymamy się na strukturze ogólnego rozwiązania jednorodnych i niejednorodnych układów liniowych równań algebraicznych. Podajmy pojęcie podstawowego układu rozwiązań i pokażmy, jak zapisuje się rozwiązanie ogólne SLAE za pomocą wektorów podstawowego układu rozwiązań. Dla lepszego zrozumienia spójrzmy na kilka przykładów.

Podsumowując, rozważymy układy równań, które można sprowadzić do równań liniowych, a także różne problemy, przy rozwiązywaniu których powstają SLAE.

Nawigacja strony.

Definicje, pojęcia, oznaczenia.

Rozważymy układy p równań algebraicznych liniowych z n nieznanymi zmiennymi (p może być równe n) postaci

Nieznane zmienne, - współczynniki (niektóre liczby rzeczywiste lub zespolone), - wyrazy swobodne (również liczby rzeczywiste lub zespolone).

Ta forma nagrywania SLAE nazywa się koordynować.

W postać matrycowa zapisanie tego układu równań ma postać,
Gdzie - macierz główna systemu, - macierz kolumnowa nieznanych zmiennych, - macierz kolumnowa wolnych terminów.

Jeśli do macierzy A dodamy macierz-kolumnę wolnych wyrazów jako (n+1)-tą kolumnę, otrzymamy tzw. rozszerzona matryca układy równań liniowych. Zazwyczaj macierz rozszerzona jest oznaczona literą T, a kolumna wolnych terminów jest oddzielona pionową linią od pozostałych kolumn, czyli

Rozwiązywanie układu liniowych równań algebraicznych nazywany zbiorem wartości nieznanych zmiennych, który zamienia wszystkie równania układu w tożsamości. Równanie macierzowe dla danych wartości nieznanych zmiennych również staje się tożsamością.

Jeśli układ równań ma co najmniej jedno rozwiązanie, nazywa się go wspólny.

Jeśli układ równań nie ma rozwiązań, nazywa się go nie wspólne.

Jeśli SLAE ma unikalne rozwiązanie, nazywa się je niektórzy; jeśli istnieje więcej niż jedno rozwiązanie, to – niepewny.

Jeśli wolne wyrazy wszystkich równań układu są równe zeru , wówczas system zostaje wywołany jednorodny, W przeciwnym razie - heterogeniczny.

Rozwiązywanie elementarnych układów liniowych równań algebraicznych.

Jeżeli liczba równań układu jest równa liczbie nieznanych zmiennych, a wyznacznik jego macierzy głównej nie jest równy zeru, wówczas takie SLAE będą nazywane podstawowy. Takie układy równań mają unikalne rozwiązanie, a w przypadku układu jednorodnego wszystkie nieznane zmienne są równe zeru.

Zaczęliśmy uczyć się takich SLAE w szkole średniej. Rozwiązując je, braliśmy jedno równanie, wyrażaliśmy jedną nieznaną zmienną w kategoriach innych i podstawialiśmy ją do pozostałych równań, następnie braliśmy następne równanie, wyrażaliśmy kolejną nieznaną zmienną i podstawialiśmy ją do innych równań i tak dalej. Lub zastosowali metodę dodawania, to znaczy dodali dwa lub więcej równań, aby wyeliminować niektóre nieznane zmienne. Nie będziemy szczegółowo omawiać tych metod, ponieważ są one zasadniczo modyfikacjami metody Gaussa.

Głównymi metodami rozwiązywania elementarnych układów równań liniowych są metoda Cramera, metoda macierzowa i metoda Gaussa. Uporządkujmy je.

Rozwiązywanie układów równań liniowych metodą Cramera.

Załóżmy, że musimy rozwiązać układ liniowych równań algebraicznych

w którym liczba równań jest równa liczbie nieznanych zmiennych, a wyznacznik macierzy głównej układu jest różny od zera, czyli .

Niech będzie wyznacznikiem głównej macierzy układu i - wyznaczniki macierzy otrzymanych z A przez podstawienie 1., 2.,…, n-te kolumna odpowiednio do kolumny wolnych członków:

Przy takim zapisie nieznane zmienne są obliczane przy użyciu wzorów metody Cramera jako . W ten sposób znajduje się rozwiązanie układu liniowych równań algebraicznych metodą Cramera.

Przykład.

Metoda Cramera .

Rozwiązanie.

Główna macierz układu ma postać . Obliczmy jego wyznacznik (jeśli to konieczne, zobacz artykuł):

Ponieważ wyznacznik macierzy głównej układu jest różny od zera, układ ma unikalne rozwiązanie, które można znaleźć metodą Cramera.

Skomponujmy i obliczmy niezbędne wyznaczniki (wyznacznik otrzymujemy zastępując pierwszą kolumnę macierzy A kolumną wyrazów wolnych, wyznacznik zastępując drugą kolumnę kolumną wyrazów wolnych, a trzecią kolumnę macierzy A kolumną wyrazów wolnych) :

Znajdowanie nieznanych zmiennych za pomocą wzorów :

Odpowiedź:

Główną wadą metody Cramera (jeśli można to nazwać wadą) jest złożoność obliczania wyznaczników, gdy liczba równań w układzie jest większa niż trzy.

Rozwiązywanie układów liniowych równań algebraicznych metodą macierzową (z wykorzystaniem macierzy odwrotnej).

Niech układ liniowych równań algebraicznych będzie dany w postaci macierzowej, gdzie macierz A ma wymiar n na n, a jej wyznacznik jest różny od zera.

Ponieważ , macierz A jest odwracalna, to znaczy istnieje macierz odwrotna. Jeśli pomnożymy obie strony równości przez lewą stronę, otrzymamy wzór na znalezienie macierzy-kolumny nieznanych zmiennych. W ten sposób otrzymaliśmy rozwiązanie układu liniowych równań algebraicznych metodą macierzową.

Przykład.

Rozwiązywać układ równań liniowych metoda matrycowa.

Rozwiązanie.

Zapiszmy układ równań w postaci macierzowej:

Ponieważ

wówczas SLAE można rozwiązać metodą macierzową. Korzystając z macierzy odwrotnej, rozwiązanie tego układu można znaleźć jako .

Skonstruujmy macierz odwrotną, korzystając z macierzy z algebraicznych dodatków elementów macierzy A (jeśli to konieczne, zobacz artykuł):

Pozostaje obliczyć macierz nieznanych zmiennych poprzez pomnożenie macierzy odwrotnej do kolumny macierzy wolnych członków (jeśli to konieczne, zobacz artykuł):

Odpowiedź:

lub w innym zapisie x 1 = 4, x 2 = 0, x 3 = -1.

Głównym problemem przy znajdowaniu rozwiązań układów liniowych równań algebraicznych metodą macierzową jest złożoność znajdowania macierzy odwrotnej, zwłaszcza dla macierzy kwadratowych rzędu wyższego niż trzeci.

Rozwiązywanie układów równań liniowych metodą Gaussa.

Załóżmy, że musimy znaleźć rozwiązanie układu n równań liniowych z n nieznanymi zmiennymi
którego wyznacznik macierzy głównej jest różny od zera.

Istota metody Gaussa polega na sekwencyjnym eliminowaniu nieznanych zmiennych: najpierw x 1 jest wykluczane ze wszystkich równań układu, zaczynając od drugiego, następnie x 2 jest wykluczane ze wszystkich równań, zaczynając od trzeciego i tak dalej, aż w układzie pozostanie tylko nieznana zmienna x n ostatnie równanie. Nazywa się ten proces przekształcania równań układu w celu sekwencyjnego eliminowania nieznanych zmiennych bezpośrednia metoda Gaussa. Po wykonaniu skoku do przodu metodą Gaussa, z ostatniego równania oblicza się x n, wykorzystując tę ​​​​wartość z przedostatniego równania, oblicza się x n-1 i tak dalej, z pierwszego równania oblicza się x 1. Nazywa się proces obliczania nieznanych zmiennych podczas przechodzenia od ostatniego równania układu do pierwszego odwrotność metody Gaussa.

Opiszmy pokrótce algorytm eliminacji nieznanych zmiennych.

Założymy, że , ponieważ zawsze możemy to osiągnąć poprzez zamianę równań układu. Wyeliminujmy nieznaną zmienną x 1 ze wszystkich równań układu, zaczynając od drugiego. W tym celu do drugiego równania układu dodajemy pierwsze pomnożone przez , do trzeciego równania dodajemy pierwsze pomnożone przez , i tak dalej, do n-tego równania dodajemy pierwsze pomnożone przez . Układ równań po takich przekształceniach przyjmie postać

gdzie i .

Doszlibyśmy do tego samego wyniku, gdybyśmy w pierwszym równaniu układu wyrazili x 1 w kategoriach innych nieznanych zmiennych i podstawieli otrzymane wyrażenie do wszystkich pozostałych równań. Zatem zmienna x 1 jest wykluczona ze wszystkich równań, zaczynając od drugiego.

Następnie postępujemy w podobny sposób, ale tylko z częścią powstałego układu, co zaznaczono na rysunku

W tym celu do trzeciego równania układu dodajemy drugie pomnożone przez , do czwartego równania dodajemy drugie pomnożone przez , i tak dalej, do n-tego równania dodajemy drugie pomnożone przez . Układ równań po takich przekształceniach przyjmie postać

gdzie i . Zatem zmienna x 2 jest wykluczona ze wszystkich równań, zaczynając od trzeciego.

Następnie przystępujemy do eliminacji niewiadomej x 3 i analogicznie postępujemy z zaznaczoną na rysunku częścią układu

Kontynuujemy zatem bezpośredni postęp metody Gaussa, aż system przyjmie formę

Od tego momentu zaczynamy odwrotność metody Gaussa: obliczamy x n z ostatniego równania jako , wykorzystując otrzymaną wartość x n z przedostatniego równania znajdujemy x n-1 i tak dalej, z pierwszego równania znajdujemy x 1 .

Przykład.

Rozwiązywać układ równań liniowych Metoda Gaussa.

Rozwiązanie.

Wykluczmy nieznaną zmienną x 1 z drugiego i trzeciego równania układu. Aby to zrobić, do obu stron drugiego i trzeciego równania dodajemy odpowiednie części pierwszego równania, odpowiednio pomnożone przez i przez:

Teraz eliminujemy x 2 z trzeciego równania, dodając do jego lewej i prawej strony lewą i prawą stronę drugiego równania, pomnożone przez:

To kończy skok do przodu w metodzie Gaussa, rozpoczynamy skok do tyłu.

Z ostatniego równania powstałego układu równań znajdujemy x 3:

Z drugiego równania otrzymujemy .

Z pierwszego równania znajdujemy pozostałą nieznaną zmienną i w ten sposób uzupełniamy odwrotność metody Gaussa.

Odpowiedź:

X 1 = 4, x 2 = 0, x 3 = -1.

Rozwiązywanie układów liniowych równań algebraicznych postaci ogólnej.

Generalnie liczba równań układu p nie pokrywa się z liczbą nieznanych zmiennych n:

Takie SLAE mogą nie mieć rozwiązań, mieć jedno rozwiązanie lub mieć nieskończenie wiele rozwiązań. To stwierdzenie dotyczy także układów równań, których główna macierz jest kwadratowa i osobliwa.

Twierdzenie Kroneckera–Capelliego.

Przed znalezieniem rozwiązania układu równań liniowych należy ustalić jego zgodność. Odpowiedź na pytanie, kiedy SLAE jest kompatybilne, a kiedy niespójne, daje Twierdzenie Kroneckera–Capelliego:
Aby układ p równań z n niewiadomymi (p może być równe n) był spójny, konieczne i wystarczające jest, aby rząd macierzy głównej układu był równy rządowi macierzy rozszerzonej, czyli , Pozycja (A) = Pozycja (T).

Rozważmy jako przykład zastosowanie twierdzenia Kroneckera – Capelliego do określenia zgodności układu równań liniowych.

Przykład.

Dowiedz się, czy układ równań liniowych ma rozwiązania.

Rozwiązanie.

. Zastosujmy metodę graniczących nieletnich. Minor drugiego rzędu różny od zera. Spójrzmy na graniczące z nim nieletnie trzeciego rzędu:

Ponieważ wszystkie graniczące nieletni trzeciego rzędu są równe zeru, ranga macierzy głównej jest równa dwa.

Z kolei ranga rozszerzonej macierzy jest równe trzy, ponieważ moll jest trzeciego rzędu

różny od zera.

Zatem, Rang(A), korzystając zatem z twierdzenia Kroneckera–Capelliego, możemy stwierdzić, że pierwotny układ równań liniowych jest niespójny.

Odpowiedź:

System nie ma rozwiązań.

Nauczyliśmy się więc ustalać niespójność systemu za pomocą twierdzenia Kroneckera–Capelliego.

Ale jak znaleźć rozwiązanie dla SLAE, jeśli zostanie ustalona jego kompatybilność?

Aby to zrobić, potrzebujemy pojęcia podstawy mniejszej macierzy i twierdzenia o rzędzie macierzy.

Nazywa się moll najwyższego rzędu macierzy A, różny od zera podstawowy.

Z definicji bazy minor wynika, że ​​jej rząd jest równy rządowi macierzy. W przypadku niezerowej macierzy A może istnieć kilka drugorzędnych baz;

Rozważmy na przykład macierz .

Wszystkie nieletnie trzeciego rzędu tej macierzy są równe zeru, ponieważ elementy trzeciego rzędu tej macierzy są sumą odpowiednich elementów pierwszego i drugiego rzędu.

Poniższe nieletni drugiego rzędu są podstawowe, ponieważ są niezerowe

Nieletni nie są podstawowe, ponieważ są równe zeru.

Twierdzenie o rangach macierzy.

Jeżeli rząd macierzy rzędu p na n jest równy r, to wszystkie elementy wierszowe (i kolumnowe) macierzy nie tworzące wybranej podstawy mniejszej są wyrażone liniowo w postaci odpowiadających im elementów wierszowych (i kolumnowych) tworzących podstawa niewielka.

Co mówi nam twierdzenie o rankingu macierzy?

Jeżeli zgodnie z twierdzeniem Kroneckera–Capelliego ustaliliśmy zgodność układu, to wybieramy dowolną bazę mniejszą macierzy głównej układu (jej rząd jest równy r) i wykluczamy z układu wszystkie równania, które spełniają nie tworzą wybranej podstawy drobnej. Uzyskane w ten sposób SLAE będzie równoważne pierwotnemu, gdyż odrzucone równania są w dalszym ciągu zbędne (zgodnie z twierdzeniem o randze macierzy są one liniową kombinacją pozostałych równań).

W efekcie po odrzuceniu zbędnych równań układu możliwe są dwa przypadki.

Jeżeli liczba równań r w otrzymanym układzie będzie równa liczbie nieznanych zmiennych, to będzie to określone i jedyne rozwiązanie można znaleźć metodą Cramera, metodą macierzową lub metodą Gaussa.

Przykład.

.

Rozwiązanie.

Ranga głównej macierzy systemu jest równe dwa, ponieważ moll jest drugiego rzędu różny od zera. Ranga rozszerzonej macierzy jest również równe dwa, ponieważ jedynym drugorzędnym trzecim rzędem jest zero

a drugorzędna drugorzędna rozważana powyżej jest różna od zera. Na podstawie twierdzenia Kroneckera–Capelliego można stwierdzić zgodność pierwotnego układu równań liniowych, gdyż Ranga(A)=Rank(T)=2.

Jako podstawę bierzemy drobne . Tworzą go współczynniki pierwszego i drugiego równania:


Trzecie równanie układu nie bierze udziału w tworzeniu podstawy moll, dlatego wykluczamy je z układu w oparciu o twierdzenie o rzędzie macierzy:


W ten sposób otrzymaliśmy elementarny układ liniowych równań algebraicznych. Rozwiążmy to metodą Cramera:


Odpowiedź:

x 1 = 1, x 2 = 2.

Jeżeli liczba równań r w wynikowym SLAE jest mniejsza niż liczba nieznanych zmiennych n, to po lewej stronie równań pozostawiamy wyrazy tworzące podstawę minor, a pozostałe wyrazy przenosimy na prawą stronę równania równania układu o przeciwnym znaku.

Wywoływane są nieznane zmienne (z nich r) pozostałe po lewej stronie równań główny.

Wywoływane są nieznane zmienne (jest n - r elementów), które znajdują się po prawej stronie bezpłatny.

Teraz wierzymy, że wolne nieznane zmienne mogą przyjmować dowolne wartości, podczas gdy r główne nieznane zmienne zostaną wyrażone poprzez wolne nieznane zmienne w unikalny sposób. Ich ekspresję można znaleźć rozwiązując wynikowy SLAE metodą Cramera, metodą macierzową lub metodą Gaussa.

Spójrzmy na to na przykładzie.

Przykład.

Rozwiązać układ liniowych równań algebraicznych .

Rozwiązanie.

Znajdźmy rangę głównej macierzy układu metodą graniczących nieletnich. Przyjmijmy 1 1 = 1 jako niezerową liczbę drugorzędną pierwszego rzędu. Zacznijmy szukać niezerowego molla drugiego rzędu graniczącego z tym mollem:


W ten sposób znaleźliśmy niezerową mollę drugiego rzędu. Zacznijmy szukać niezerowej granicy moll trzeciego rzędu:


Zatem ranga głównej macierzy wynosi trzy. Ranga rozszerzonej macierzy jest również równa trzy, czyli system jest spójny.

Jako podstawę przyjmujemy znalezioną niezerową mollę trzeciego rzędu.

Dla przejrzystości pokazujemy elementy tworzące podstawę moll:


Wyrazy związane z mollą bazową pozostawiamy po lewej stronie równań układu, a resztę z przeciwnymi znakami przenosimy na prawą stronę:


Dajmy wolnym nieznanym zmiennym x 2 i x 5 dowolne wartości, czyli akceptujemy , gdzie są dowolnymi liczbami. W takim przypadku SLAE przybierze formę


Rozwiążmy powstały elementarny układ liniowych równań algebraicznych metodą Cramera:


Stąd, .

W swojej odpowiedzi nie zapomnij wskazać wolnych nieznanych zmiennych.

Odpowiedź:

Gdzie są liczby dowolne.

Podsumujmy.

Aby rozwiązać układ ogólnych równań algebraicznych liniowych, najpierw określamy jego zgodność za pomocą twierdzenia Kroneckera – Capelliego. Jeśli ranga macierzy głównej nie jest równa rangi macierzy rozszerzonej, wówczas stwierdzamy, że system jest niekompatybilny.

Jeżeli ranga macierzy głównej jest równa rangi macierzy rozszerzonej, wówczas wybieramy moll bazowy i odrzucamy równania układu, które nie biorą udziału w tworzeniu wybranego molla bazowego.

Jeśli rząd moll podstawy jest równy liczbie nieznanych zmiennych, wówczas SLAE ma unikalne rozwiązanie, które można znaleźć dowolną znaną nam metodą.

Jeśli rząd podstawy mniejszej jest mniejszy niż liczba nieznanych zmiennych, to po lewej stronie równań układu pozostawiamy wyrazy z głównymi nieznanymi zmiennymi, pozostałe wyrazy przenosimy na prawą stronę i podajemy dowolne wartości wolne nieznane zmienne. Z powstałego układu równań liniowych wyznaczamy główne nieznane zmienne, stosując metodę Cramera, metodę macierzową lub metodę Gaussa.

Metoda Gaussa rozwiązywania układów liniowych równań algebraicznych o postaci ogólnej.

Metodę Gaussa można zastosować do rozwiązywania układów liniowych równań algebraicznych dowolnego rodzaju bez uprzedniego sprawdzania ich pod kątem zgodności. Proces sekwencyjnej eliminacji nieznanych zmiennych pozwala wyciągnąć wniosek zarówno o zgodności, jak i niezgodności SLAE, a jeśli istnieje rozwiązanie, umożliwia jego znalezienie.

Z obliczeniowego punktu widzenia preferowana jest metoda Gaussa.

Jej szczegółowy opis i przeanalizowane przykłady można znaleźć w artykule Metoda Gaussa rozwiązywania układów ogólnych równań algebraicznych liniowych.

Zapisywanie rozwiązań ogólnych jednorodnych i niejednorodnych liniowych układów algebraicznych z wykorzystaniem wektorów podstawowego układu rozwiązań.

W tej sekcji omówimy jednoczesne jednorodne i niejednorodne układy liniowych równań algebraicznych, które mają nieskończoną liczbę rozwiązań.

Zajmijmy się najpierw systemami jednorodnymi.

Podstawowy system rozwiązań jednorodny układ p równań algebraicznych liniowych z n nieznanymi zmiennymi to zbiór (n – r) liniowo niezależnych rozwiązań tego układu, gdzie r jest rządem mniejszej podstawy macierzy głównej układu.

Jeśli oznaczymy liniowo niezależne rozwiązania jednorodnego SLAE jako X (1) , X (2) , …, X (n-r) (X (1) , X (2) , …, X (n-r) są macierzami kolumnowymi o wymiarze n przez 1) , wówczas ogólne rozwiązanie tego jednorodnego układu jest reprezentowane jako liniowa kombinacja wektorów podstawowego układu rozwiązań o dowolnych stałych współczynnikach C 1, C 2, ..., C (n-r), to znaczy .

Co oznacza termin ogólne rozwiązanie jednorodnego układu liniowych równań algebraicznych (oroslau)?

Znaczenie jest proste: wzór określa wszystkie możliwe rozwiązania pierwotnego SLAE, innymi słowy, przyjmując dowolny zbiór wartości dowolnych stałych C 1, C 2, ..., C (n-r), korzystając ze wzoru, który zrobimy otrzymać jedno z rozwiązań pierwotnego jednorodnego SLAE.

Zatem jeśli znajdziemy podstawowy system rozwiązań, wówczas możemy zdefiniować wszystkie rozwiązania tego jednorodnego SLAE jako .

Pokażmy proces konstruowania podstawowego systemu rozwiązań do jednorodnego SLAE.

Wybieramy bazę mniejszą pierwotnego układu równań liniowych, wykluczamy z układu wszystkie pozostałe równania i przenosimy wszystkie wyrazy zawierające wolne nieznane zmienne na prawe strony równań układu o przeciwnych znakach. Niewiadomym swobodnym nadajmy wartości 1,0,0,...,0 i obliczmy główne niewiadome rozwiązując w dowolny sposób otrzymany elementarny układ równań liniowych, na przykład metodą Cramera. W rezultacie otrzymamy X (1) - pierwsze rozwiązanie układu podstawowego. Jeśli podamy wolnym niewiadomym wartości 0,1,0,0,…,0 i obliczymy główne niewiadome, otrzymamy X (2) . I tak dalej. Jeżeli niewiadomym wolnym przypiszemy wartości 0,0,…,0,1 i obliczymy niewiadome główne, otrzymamy X (n-r). W ten sposób zostanie skonstruowany podstawowy system rozwiązań jednorodnego SLAE, a jego rozwiązanie ogólne będzie można zapisać w postaci .

W przypadku niejednorodnych układów liniowych równań algebraicznych rozwiązanie ogólne jest reprezentowane w postaci , gdzie jest rozwiązaniem ogólnym odpowiedniego układu jednorodnego i jest rozwiązaniem szczególnym pierwotnego niejednorodnego SLAE, które otrzymujemy podając wartości niewiadomym wolnym ​0,0,…,0 i obliczenie wartości głównych niewiadomych.

Spójrzmy na przykłady.

Przykład.

Znajdź podstawowy układ rozwiązań i rozwiązanie ogólne jednorodnego układu liniowych równań algebraicznych .

Rozwiązanie.

Ranga macierzy głównej jednorodnych układów równań liniowych jest zawsze równa rangi macierzy rozszerzonej. Znajdźmy rząd macierzy głównej, stosując metodę graniczących nieletnich. Jako niezerową liczbę drugorzędną pierwszego rzędu bierzemy element a 1 1 = 9 macierzy głównej układu. Znajdźmy graniczący niezerowy moll drugiego rzędu:

Znaleziono moll drugiego rzędu, różny od zera. Przejdźmy przez nieletnie trzeciego rzędu graniczące z nim w poszukiwaniu niezerowej jedynki:

Wszystkie nieletnie graniczące trzeciego rzędu są równe zeru, dlatego ranga macierzy głównej i rozszerzonej jest równa dwa. Weźmy. Dla jasności zwróćmy uwagę na elementy systemu, które go tworzą:

Trzecie równanie pierwotnego SLAE nie uczestniczy w tworzeniu podstawy moll, dlatego można je wykluczyć:

Wyrazy zawierające główne niewiadome pozostawiamy po prawej stronie równań, a wyrazy z wolnymi niewiadomymi przenosimy na prawe strony:

Skonstruujmy podstawowy układ rozwiązań pierwotnego jednorodnego układu równań liniowych. Podstawowy system rozwiązań tego SLAE składa się z dwóch rozwiązań, ponieważ pierwotny SLAE zawiera cztery nieznane zmienne, a rząd jego molowej podstawy jest równy dwa. Aby znaleźć X (1), wolnym nieznanym zmiennym nadajemy wartości x 2 = 1, x 4 = 0, następnie znajdujemy główne niewiadome z układu równań
.

Układ m równań liniowych z n niewiadomymi zwany systemem formy

Gdzie ij I b ja (I=1,…,M; B=1,…,N) to kilka znanych liczb, i x 1 ,…,x n– nieznany. W wyznaczaniu współczynników ij pierwszy indeks I oznacza numer równania, a drugi J– liczba niewiadomych, przy której stoi ten współczynnik.

Współczynniki niewiadomych zapiszemy w postaci macierzy , który nazwiemy macierz układu.

Liczby po prawej stronie równań to b 1 ,…,b m są nazywane wolni członkowie.

Całość N takty muzyczne do 1 ,…,c n zwany decyzja danego układu, jeżeli każde równanie układu staje się równością po podstawieniu do niego liczb do 1 ,…,c n zamiast odpowiednich niewiadomych x 1 ,…,x n.

Naszym zadaniem będzie znalezienie rozwiązań dla systemu. W takim przypadku mogą wystąpić trzy sytuacje:

Układ równań liniowych, który ma co najmniej jedno rozwiązanie nazywa się wspólny. W przeciwnym razie, tj. jeśli system nie ma rozwiązań, nazywa się go nie wspólne.

Zastanówmy się, jak znaleźć rozwiązania dla systemu.

METODA MATRYCOWA ROZWIĄZYWANIA UKŁADÓW RÓWNAŃ LINIOWYCH

Macierze umożliwiają krótkie zapisanie układu równań liniowych. Niech będzie dany układ 3 równań z trzema niewiadomymi:

Rozważmy macierz systemu 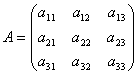i macierze kolumny nieznanych i wolnych terminów

Znajdźmy pracę

te. w wyniku iloczynu otrzymujemy lewe strony równań tego układu. Następnie korzystając z definicji równości macierzy układ ten można zapisać w postaci

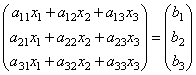lub krócej A∙X=B.

Oto macierze A I B są znane, oraz macierz X nieznany. Trzeba go znaleźć, bo... jego elementy są rozwiązaniem tego systemu. To równanie nazywa się równanie macierzowe.

Niech wyznacznik macierzy będzie różny od zera | A| ≠ 0. Następnie równanie macierzowe rozwiązuje się w następujący sposób. Pomnóż obie strony równania po lewej stronie przez macierz A-1, odwrotność macierzy A: . Ponieważ A -1 A = E I mi∙X = X, wówczas otrzymujemy rozwiązanie równania macierzowego w postaci X = A -1 B .

Należy zauważyć, że ponieważ macierz odwrotną można znaleźć tylko dla macierzy kwadratowych, metoda macierzowa może rozwiązać tylko te układy, w których liczba równań pokrywa się z liczbą niewiadomych. Jednakże macierzowy zapis układu jest możliwy również w przypadku, gdy liczba równań nie jest równa liczbie niewiadomych, wówczas macierz A nie będzie kwadratowy i dlatego nie da się znaleźć rozwiązania układu w postaci X = A -1 B.

Przykłady. Rozwiązywać układy równań.

REGUŁA CRAMERA

Rozważmy układ 3 równań liniowych z trzema niewiadomymi:

Wyznacznik trzeciego rzędu odpowiadający macierzy układu, tj. złożony ze współczynników niewiadomych,

zwany wyznacznik systemu.

Skomponujmy jeszcze trzy wyznaczniki w następujący sposób: zamień kolumny 1, 2 i 3 w wyznaczniku D kolejno na kolumnę wolnych terminów

Następnie możemy udowodnić następujący wynik.

Twierdzenie (reguła Cramera). Jeżeli wyznacznik układu Δ ≠ 0, to rozpatrywany układ ma jedno i tylko jedno rozwiązanie, a

Dowód. Rozważmy więc układ trzech równań z trzema niewiadomymi. Pomnóżmy pierwsze równanie układu przez dopełnienie algebraiczne 11 element 11, 2 równanie – włączone 21 i 3. – dalej 31:

Dodajmy te równania:

Przyjrzyjmy się każdemu z nawiasów i prawej stronie tego równania. Według twierdzenia o rozwinięciu wyznacznika w elementach pierwszej kolumny

Podobnie można wykazać, że i .

Wreszcie łatwo to zauważyć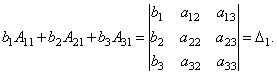

Otrzymujemy zatem równość: .

Stąd, .

Równości i wyprowadza się w podobny sposób, z czego wynika stwierdzenie twierdzenia.

Zauważamy zatem, że jeśli wyznacznik układu Δ ≠ 0, to układ ma rozwiązanie jednoznaczne i odwrotnie. Jeżeli wyznacznik układu jest równy zeru, to układ albo ma nieskończoną liczbę rozwiązań, albo nie ma żadnych rozwiązań, tj. niezgodny.

Przykłady. Rozwiązać układ równań

METODA GAUssa

Omówione wcześniej metody można zastosować do rozwiązania tylko tych układów, w których liczba równań pokrywa się z liczbą niewiadomych, a wyznacznik układu musi być różny od zera. Metoda Gaussa jest bardziej uniwersalna i odpowiednia dla układów o dowolnej liczbie równań. Polega ona na konsekwentnym eliminowaniu niewiadomych z równań układu.

Rozważmy ponownie układ trzech równań z trzema niewiadomymi:

.

Pierwsze równanie pozostawimy bez zmian, a z drugiego i trzeciego wykluczymy terminy zawierające x 1. Aby to zrobić, podziel drugie równanie przez A 21 i pomnóż przez – A 11, a następnie dodaj go do pierwszego równania. Podobnie dzielimy trzecie równanie przez A 31 i pomnóż przez – A 11, a następnie dodaj go do pierwszego. W efekcie oryginalny system przyjmie postać:

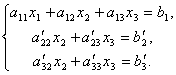
Teraz z ostatniego równania eliminujemy termin zawierający x 2. Aby to zrobić, podziel trzecie równanie przez, pomnóż przez drugie i dodaj z drugim. Wtedy będziemy mieli układ równań:

Stąd z ostatniego równania łatwo jest znaleźć x 3, to z drugiego równania x 2 i wreszcie, od 1-go - x 1.

W przypadku stosowania metody Gaussa równania można w razie potrzeby zamienić.

Często zamiast pisać nowy układ równań ograniczają się do napisania rozszerzonej macierzy układu:

a następnie doprowadź go do postaci trójkątnej lub ukośnej za pomocą elementarnych przekształceń.

DO elementarne przemiany macierze obejmują następujące przekształcenia:

1. przestawianie wierszy lub kolumn;
2. mnożenie ciągu przez liczbę inną niż zero;
3. dodanie innych linii do jednej linii.

Przykłady: Rozwiązywać układy równań metodą Gaussa.

Zatem układ ma nieskończoną liczbę rozwiązań.

Metoda Gaussa, zwana także metodą sekwencyjnej eliminacji niewiadomych, jest następująca. Za pomocą przekształceń elementarnych układ równań liniowych doprowadza się do takiej postaci, że jego macierz współczynników okazuje się być trapezoidalny (taki sam jak trójkątny lub schodkowy) lub zbliżony do trapezowego (skok bezpośredni metody Gaussa, zwany dalej po prostu skokiem prostym). Przykład takiego układu i jego rozwiązania przedstawiono na powyższym rysunku.

W takim układzie ostatnie równanie zawiera tylko jedną zmienną i można jednoznacznie znaleźć jej wartość. Wartość tej zmiennej jest następnie podstawiona do poprzedniego równania ( odwrotność metody Gaussa , potem tylko odwrotnie), z którego zostanie znaleziona poprzednia zmienna i tak dalej.

Jak widzimy, w układzie trapezowym (trójkątnym) trzecie równanie nie zawiera już zmiennych y I X, a drugie równanie jest zmienną X .

Gdy macierz układu przybierze kształt trapezu, zrozumienie zagadnienia kompatybilności układu, określenie liczby rozwiązań i znalezienie samych rozwiązań nie jest już trudne.

Zalety metody:

1. przy rozwiązywaniu układów równań liniowych zawierających więcej niż trzy równania i niewiadome metoda Gaussa nie jest tak uciążliwa jak metoda Cramera, ponieważ rozwiązywanie metodą Gaussa wymaga mniej obliczeń;
2. metodą Gaussa można rozwiązywać nieokreślone układy równań liniowych, czyli takie, które mają rozwiązanie ogólne (i przeanalizujemy je w tej lekcji), a stosując metodę Cramera możemy jedynie stwierdzić, że układ jest niewyznaczalny;
3. potrafisz rozwiązywać układy równań liniowych, w których liczba niewiadomych nie jest równa liczbie równań (przeanalizujemy je również w tej lekcji);
4. Metoda opiera się na metodach elementarnych (szkolnych) - metodzie podstawiania niewiadomych i metodzie dodawania równań, o których pisaliśmy w odpowiednim artykule.

Aby każdy zrozumiał prostotę, z jaką rozwiązuje się trapezowe (trójkątne, schodkowe) układy równań liniowych, przedstawiamy rozwiązanie takiego układu wykorzystując ruch odwrotny. Szybkie rozwiązanie tego układu pokazano na obrazku na początku lekcji.

Przykład 1. Rozwiąż układ równań liniowych, stosując odwrotność:

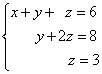
Rozwiązanie. W tym układzie trapezowym zmienna z można jednoznacznie znaleźć na podstawie trzeciego równania. Podstawiamy jego wartość do drugiego równania i otrzymujemy wartość zmiennej y:

Teraz znamy wartości dwóch zmiennych - z I y. Podstawiamy je do pierwszego równania i otrzymujemy wartość zmiennej X:

Z poprzednich kroków zapisujemy rozwiązanie układu równań:

Aby otrzymać taki trapezowy układ równań liniowych, który rozwiązaliśmy w bardzo prosty sposób, konieczne jest zastosowanie skoku do przodu związanego z elementarnymi transformacjami układu równań liniowych. To również nie jest bardzo trudne.

Przekształcenia elementarne układu równań liniowych

Powtarzając szkolną metodę algebraicznego dodawania równań układu, odkryliśmy, że do jednego z równań układu można dodać kolejne równanie układu, a każde z równań można pomnożyć przez jakąś liczbę. W rezultacie otrzymujemy układ równań liniowych równoważny temu. W nim jedno równanie zawierało już tylko jedną zmienną, podstawiając jej wartość do innych równań, dochodzimy do rozwiązania. Dodatek taki jest jednym z rodzajów elementarnej transformacji układu. Stosując metodę Gaussa, możemy zastosować kilka rodzajów transformacji.

Powyższa animacja pokazuje, jak układ równań stopniowo przekształca się w trapezoidalny. To znaczy ten, który widziałeś w pierwszej animacji i przekonałeś się, że łatwo jest znaleźć w nim wartości wszystkich niewiadomych. Jak przeprowadzić taką transformację i oczywiście przykłady zostaną omówione dalej.

Przy rozwiązywaniu układów równań liniowych z dowolną liczbą równań i niewiadomych w układzie równań i w rozszerzonej macierzy układu Móc:

1. zmienić układ linii (wspomniano o tym na samym początku tego artykułu);
2. jeżeli inne przekształcenia dają wiersze równe lub proporcjonalne, można je usunąć, za wyjątkiem jednego;
3. usuń wiersze „zero”, w których wszystkie współczynniki są równe zero;
4. pomnożyć lub podzielić dowolny ciąg przez określoną liczbę;
5. do dowolnej linii dodaj kolejną linię pomnożoną przez określoną liczbę.

W wyniku przekształceń otrzymujemy równoważny temu układ równań liniowych.

Algorytm i przykłady rozwiązywania układu równań liniowych z macierzą kwadratową układu metodą Gaussa

Rozważmy najpierw rozwiązanie układów równań liniowych, w których liczba niewiadomych jest równa liczbie równań. Macierz takiego systemu jest kwadratowa, to znaczy liczba w niej wierszy jest równa liczbie kolumn.

Przykład 2. Rozwiązać układ równań liniowych metodą Gaussa

Rozwiązując układy równań liniowych metodami szkolnymi, mnożyliśmy jedno z równań wyraz po wyrazie, tak że współczynniki pierwszej zmiennej w obu równaniach były liczbami przeciwnymi. Podczas dodawania równań zmienna ta jest eliminowana. Metoda Gaussa działa podobnie.

Aby uprościć wygląd rozwiązania utwórzmy rozszerzoną macierz układu:

W tej macierzy współczynniki niewiadomych znajdują się po lewej stronie przed linią pionową, a wyrazy wolne po prawej stronie za linią pionową.

Dla wygody dzielenia współczynników dla zmiennych (w celu uzyskania dzielenia przez jedność) Zamieńmy pierwszy i drugi wiersz macierzy systemowej. Otrzymujemy układ równoważny temu, gdyż w układzie równań liniowych równania można zamieniać:

Korzystając z nowego pierwszego równania wyeliminuj zmienną X z drugiego i wszystkich kolejnych równań. W tym celu do drugiego wiersza macierzy dodajemy pierwszy wiersz pomnożony przez (w naszym przypadku przez ), do trzeciego wiersza - pierwszy wiersz pomnożony przez (w naszym przypadku przez ).

Jest to możliwe, ponieważ

Gdyby w naszym układzie było więcej niż trzy równania, to do wszystkich kolejnych równań musielibyśmy dodać pierwszą linię pomnożoną przez stosunek odpowiednich współczynników, wzięty ze znakiem minus.

W rezultacie otrzymujemy macierz równoważną temu układowi nowego układu równań, w którym wszystkie równania, począwszy od drugiego nie zawierają zmiennej X :

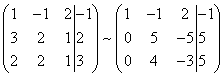
Aby uprościć drugą linię powstałego układu, mnożymy ją przez i ponownie otrzymujemy macierz układu równań równoważnego temu układowi:

Teraz, zachowując niezmienione pierwsze równanie powstałego układu, korzystając z drugiego równania eliminujemy zmienną y ze wszystkich kolejnych równań. W tym celu do trzeciego wiersza macierzy systemowej dodajemy drugi wiersz pomnożony przez (w naszym przypadku przez ).

Gdyby w naszym układzie było więcej niż trzy równania, wówczas do wszystkich kolejnych równań musielibyśmy dodać drugą linię, pomnożoną przez stosunek odpowiednich współczynników wziętych ze znakiem minus.

W rezultacie ponownie otrzymujemy macierz układu równoważnego temu układowi równań liniowych:

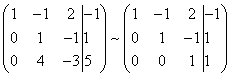
Otrzymaliśmy równoważny trapezoidalny układ równań liniowych:

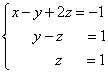
Jeżeli liczba równań i zmiennych jest większa niż w naszym przykładzie, to proces sekwencyjnego eliminowania zmiennych trwa do momentu, aż macierz układu stanie się trapezoidalna, jak w naszym przykładzie demonstracyjnym.

Rozwiązanie znajdziemy „od końca” – ruch odwrotny. Do tego z ostatniego równania, które wyznaczamy z:
.
Podstawiając tę ​​wartość do poprzedniego równania, znajdziemy y:

Z pierwszego równania znajdziemy X:

Odpowiedź: rozwiązaniem tego układu równań jest .

: w tym przypadku zostanie udzielona ta sama odpowiedź, jeśli system ma unikalne rozwiązanie. Jeśli układ ma nieskończoną liczbę rozwiązań, to będzie to odpowiedź i to jest temat piątej części tej lekcji.

Rozwiąż samodzielnie układ równań liniowych metodą Gaussa, a następnie przyjrzyj się rozwiązaniu

Tutaj znowu mamy przykład spójnego i określonego układu równań liniowych, w którym liczba równań jest równa liczbie niewiadomych. Różnica w stosunku do naszego przykładu demonstracyjnego algorytmu polega na tym, że istnieją już cztery równania i cztery niewiadome.

Przykład 4. Rozwiąż układ równań liniowych metodą Gaussa:

Teraz musisz użyć drugiego równania, aby wyeliminować zmienną z kolejnych równań. Przeprowadźmy prace przygotowawcze. Aby było to wygodniejsze ze stosunkiem współczynników, musisz uzyskać jeden w drugiej kolumnie drugiego rzędu. Aby to zrobić, odejmij trzecią linię od drugiej linii i pomnóż wynikową drugą linię przez -1.

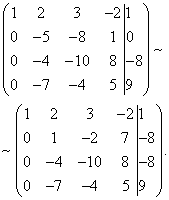
Przeprowadźmy teraz faktyczną eliminację zmiennej z trzeciego i czwartego równania. Aby to zrobić, dodaj drugą linię pomnożoną przez , do trzeciej linii, a drugą, pomnożoną przez , do czwartej linii.

Teraz, korzystając z trzeciego równania, eliminujemy zmienną z czwartego równania. Aby to zrobić, dodaj trzecią linię do czwartej linii, pomnożoną przez . Otrzymujemy rozszerzoną macierz trapezową.

Otrzymaliśmy układ równań, któremu dany układ jest równoważny:

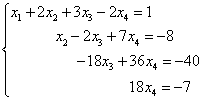
W konsekwencji otrzymane i dane systemy są zgodne i określone. Ostateczne rozwiązanie znajdujemy „od końca”. Z czwartego równania możemy bezpośrednio wyrazić wartość zmiennej „x-cztery”:

Podstawiamy tę wartość do trzeciego równania układu i otrzymujemy

,

,

Wreszcie podstawienie wartości

Pierwsze równanie daje

,

gdzie znajdziemy „najpierw x”:

Odpowiedź: ten układ równań ma unikalne rozwiązanie .

Rozwiązanie układu można także sprawdzić na kalkulatorze, stosując metodę Cramera: w tym przypadku taka sama odpowiedź zostanie udzielona, ​​jeśli układ ma unikalne rozwiązanie.

Rozwiązywanie problemów stosowanych metodą Gaussa na przykładzie zadania na stopach

Układy równań liniowych służą do modelowania rzeczywistych obiektów w świecie fizycznym. Rozwiążmy jeden z tych problemów - stopy. Podobnymi problemami są problemy dotyczące mieszanin, kosztu lub udziału poszczególnych towarów w grupie towarów i tym podobne.

Przykład 5. Trzy kawałki stopu mają łączną masę 150 kg. Pierwszy stop zawiera 60% miedzi, drugi - 30%, trzeci - 10%. Ponadto w stopie drugim i trzecim łącznie jest o 28,4 kg mniej miedzi niż w stopie pierwszym, a w stopie trzecim jest o 6,2 kg mniej miedzi niż w stopie drugim. Znajdź masę każdego kawałka stopu.

Rozwiązanie. Tworzymy układ równań liniowych:

Mnożymy drugie i trzecie równanie przez 10, otrzymujemy równoważny układ równań liniowych:

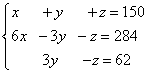
Tworzymy rozszerzoną macierz systemu:

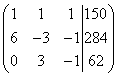
Uwaga, prosto. Dodając (w naszym przypadku odejmując) jeden wiersz pomnożony przez liczbę (stosujemy dwukrotnie), na rozszerzonej macierzy układu zachodzą następujące przekształcenia:

Bezpośredni ruch dobiegł końca. Otrzymaliśmy rozszerzoną macierz trapezową.

Stosujemy ruch odwrotny. Znajdujemy rozwiązanie od końca. Widzimy to.

Z drugiego równania znajdujemy

Z trzeciego równania -

Rozwiązanie układu można także sprawdzić na kalkulatorze, stosując metodę Cramera: w tym przypadku ta sama odpowiedź zostanie udzielona, ​​jeśli układ ma unikalne rozwiązanie.

O prostocie metody Gaussa świadczy fakt, że wynalezienie jej zajęło niemieckiemu matematykowi Carlowi Friedrichowi Gaussowi zaledwie 15 minut. Oprócz metody nazwanej jego imieniem, z dzieł Gaussa znane jest powiedzenie „Nie mylmy tego, co wydaje nam się niewiarygodne i nienaturalne, z tym, co absolutnie niemożliwe” - rodzaj krótkiej instrukcji dokonywania odkryć.

W wielu stosowanych problemach może nie być trzeciego ograniczenia, czyli trzeciego równania, wówczas trzeba rozwiązać układ dwóch równań z trzema niewiadomymi metodą Gaussa lub odwrotnie, jest mniej niewiadomych niż równań. Zaczniemy teraz rozwiązywać takie układy równań.

Za pomocą metody Gaussa można określić, czy dany system jest kompatybilny, czy nie N równania liniowe z N zmienne.

Metoda Gaussa i układy równań liniowych o nieskończonej liczbie rozwiązań

Następnym przykładem jest spójny, ale niewyznaczalny układ równań liniowych, czyli mający nieskończoną liczbę rozwiązań.

Po wykonaniu przekształceń w rozszerzonej macierzy systemu (przestawienie wierszy, pomnożenie i podzielenie wierszy przez określoną liczbę, dodanie kolejnego do jednego wiersza) mogły pojawić się wiersze formularza

Jeśli we wszystkich równaniach mających postać

Wyrazy wolne są równe zeru, oznacza to, że układ jest niepewny, czyli ma nieskończoną liczbę rozwiązań, a równania tego typu są „zbędne” i wykluczamy je z układu.

Przykład 6.

Rozwiązanie. Stwórzmy rozszerzoną macierz układu. Następnie korzystając z pierwszego równania eliminujemy zmienną z kolejnych równań. Aby to zrobić, dodaj do drugiej, trzeciej i czwartej linii pierwszą, pomnożoną przez:

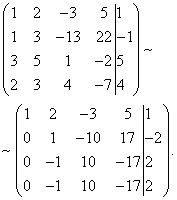
Teraz dodajmy drugą linię do trzeciej i czwartej.

W rezultacie dochodzimy do systemu

Ostatnie dwa równania zamieniły się w równania postaci. Równania te są spełnione dla dowolnej wartości niewiadomych i można je odrzucić.

Aby spełnić drugie równanie, możemy wybrać dowolne wartości dla i , wówczas wartość dla zostanie określona jednoznacznie: . Z pierwszego równania można również jednoznacznie znaleźć wartość: .

Zarówno dane, jak i ostatnie systemy są spójne, ale niepewne, a także formuły

dla dowolnych i dają nam wszystkie rozwiązania danego układu.

Metoda Gaussa i układy równań liniowych bez rozwiązań

Następnym przykładem jest niespójny układ równań liniowych, czyli taki, który nie ma rozwiązań. Odpowiedź na takie problemy formułuje się w następujący sposób: system nie ma rozwiązań.

Jak już wspomniano w nawiązaniu do pierwszego przykładu, po wykonaniu przekształceń w rozszerzonej macierzy układu mogą pojawić się wiersze formularza

odpowiadające równaniu postaci

Jeżeli wśród nich jest przynajmniej jedno równanie z niezerowym wyrazem wolnym (tj. ), to ten układ równań jest niespójny, to znaczy nie ma rozwiązań i jego rozwiązanie jest zakończone.

Przykład 7. Rozwiąż układ równań liniowych metodą Gaussa:

Rozwiązanie. Tworzymy rozbudowaną matrycę systemu. Korzystając z pierwszego równania, wykluczamy zmienną z kolejnych równań. Aby to zrobić, dodaj pierwszą linię pomnożoną przez drugą linię, pierwszą linię pomnożoną przez trzecią linię i pierwszą linię pomnożoną przez czwartą linię.

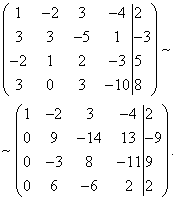
Teraz musisz użyć drugiego równania, aby wyeliminować zmienną z kolejnych równań. Aby otrzymać całkowite stosunki współczynników, zamieniamy drugi i trzeci wiersz rozszerzonej macierzy układu.

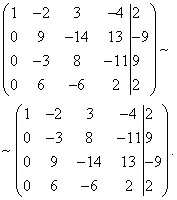
Aby wykluczyć trzecie i czwarte równanie, dodaj drugie pomnożone przez , do trzeciej linii, a drugie pomnożone przez , do czwartej linii.

Teraz, korzystając z trzeciego równania, eliminujemy zmienną z czwartego równania. Aby to zrobić, dodaj trzecią linię do czwartej linii, pomnożoną przez .

Dany system jest zatem równoważny następującemu:

Powstały układ jest niespójny, ponieważ jego ostatniego równania nie mogą spełnić żadne wartości niewiadomych. Zatem układ ten nie ma rozwiązań.

Zachowanie Twojej prywatności jest dla nas ważne. Z tego powodu opracowaliśmy Politykę prywatności, która opisuje, w jaki sposób wykorzystujemy i przechowujemy Twoje dane. Zapoznaj się z naszymi praktykami dotyczącymi prywatności i daj nam znać, jeśli masz jakiekolwiek pytania.

Gromadzenie i wykorzystywanie danych osobowych

Dane osobowe to dane, które można wykorzystać do identyfikacji konkretnej osoby lub skontaktowania się z nią.

Możesz zostać poproszony o podanie swoich danych osobowych w dowolnym momencie kontaktu z nami.

Poniżej znajduje się kilka przykładów rodzajów danych osobowych, które możemy gromadzić i sposobu, w jaki możemy je wykorzystywać.

Jakie dane osobowe zbieramy:

• Kiedy składasz wniosek na stronie, możemy zbierać różne informacje, w tym Twoje imię i nazwisko, numer telefonu, adres e-mail itp.

Jak wykorzystujemy Twoje dane osobowe:

• Gromadzone przez nas dane osobowe pozwalają nam kontaktować się z Tobą w sprawie wyjątkowych ofert, promocji i innych wydarzeń oraz nadchodzących wydarzeń.
• Od czasu do czasu możemy wykorzystywać Twoje dane osobowe do wysyłania ważnych powiadomień i komunikatów.
• Możemy również wykorzystywać dane osobowe do celów wewnętrznych, takich jak przeprowadzanie audytów, analiza danych i różnych badań w celu ulepszenia świadczonych przez nas usług i przedstawienia rekomendacji dotyczących naszych usług.
• Jeśli bierzesz udział w losowaniu nagród, konkursie lub podobnej promocji, możemy wykorzystać podane przez Ciebie informacje w celu administrowania takimi programami.

Ujawnianie informacji osobom trzecim

Nie udostępniamy otrzymanych od Państwa informacji osobom trzecim.

Wyjątki:

• Jeżeli jest to konieczne – zgodnie z prawem, procedurą sądową, w postępowaniu sądowym i/lub na podstawie publicznych żądań lub wniosków organów rządowych Federacji Rosyjskiej – do ujawnienia Twoich danych osobowych. Możemy również ujawnić informacje o Tobie, jeśli uznamy, że takie ujawnienie jest konieczne lub odpowiednie ze względów bezpieczeństwa, egzekwowania prawa lub innych celów ważnych dla społeczeństwa.
• W przypadku reorganizacji, fuzji lub sprzedaży możemy przekazać zebrane dane osobowe odpowiedniej następczej stronie trzeciej.

Ochrona danych osobowych

Podejmujemy środki ostrożności – w tym administracyjne, techniczne i fizyczne – aby chronić Twoje dane osobowe przed utratą, kradzieżą i niewłaściwym wykorzystaniem, a także nieuprawnionym dostępem, ujawnieniem, zmianą i zniszczeniem.

Szanowanie Twojej prywatności na poziomie firmy

Aby zapewnić bezpieczeństwo Twoich danych osobowych, przekazujemy naszym pracownikom standardy dotyczące prywatności i bezpieczeństwa oraz rygorystycznie egzekwujemy praktyki dotyczące prywatności.

W dalszym ciągu zajmujemy się układami równań liniowych. Do tej pory rozważaliśmy systemy, które mają unikalne rozwiązanie. Takie układy można rozwiązać w dowolny sposób: metodą podstawieniową("szkoła"), według wzorów Cramera, metoda macierzowa, Metoda Gaussa. Jednak w praktyce powszechne są jeszcze dwa przypadki:

1) układ jest niespójny (nie ma rozwiązań);

2) układ ma nieskończenie wiele rozwiązań.

W przypadku tych układów stosuje się najbardziej uniwersalną ze wszystkich metod rozwiązań - Metoda Gaussa. W rzeczywistości metoda „szkolna” również doprowadzi do odpowiedzi, ale w wyższej matematyce zwyczajowo stosuje się metodę Gaussa sekwencyjnej eliminacji niewiadomych. Ci, którzy nie są zaznajomieni z algorytmem metody Gaussa, powinni najpierw przestudiować lekcję Metoda Gaussa

Same transformacje macierzy elementarnych są dokładnie takie same, różnica będzie polegać na zakończeniu rozwiązania. Najpierw spójrzmy na kilka przykładów, gdy układ nie ma rozwiązań (niespójny).

Przykład 1

Co od razu rzuca się w oczy w tym systemie? Liczba równań jest mniejsza niż liczba zmiennych. Istnieje twierdzenie, które stwierdza: „Jeśli liczba równań w układzie jest mniejsza niż liczba zmiennych, wówczas układ jest albo niespójny, albo ma nieskończenie wiele rozwiązań.” I jedyne, co pozostaje, to się dowiedzieć.

Początek rozwiązania jest zupełnie zwyczajny – zapisujemy rozszerzoną macierz układu i za pomocą elementarnych przekształceń doprowadzamy ją do postaci krokowej:

(1). W lewym górnym kroku musimy uzyskać (+1) lub (–1). W pierwszej kolumnie nie ma takich liczb, więc przestawianie wierszy nic nie da. Jednostka będzie musiała się zorganizować sama, a można to zrobić na kilka sposobów. Zrobiliśmy to. Do pierwszej linii dodajemy trzecią linię pomnożoną przez (–1).

(2). Teraz w pierwszej kolumnie otrzymujemy dwa zera. Do drugiej linii dodajemy pierwszą linię pomnożoną przez 3. Do trzeciej linii dodajemy pierwszą linię pomnożoną przez 5.

(3). Po zakończeniu transformacji zawsze warto sprawdzić, czy możliwe jest uproszczenie powstałych ciągów znaków? Móc. Drugą linię dzielimy przez 2, jednocześnie uzyskując żądaną linię (–1) w drugim kroku. Podziel trzecią linię przez (–3).

(4). Dodaj drugą linię do trzeciej linii. Chyba każdy zauważył złą linię wynikającą z elementarnych przekształceń:

. Jasne jest, że tak nie może być.

Rzeczywiście, przepiszemy otrzymaną macierz

wracając do układu równań liniowych:

Jeżeli w wyniku elementarnych przekształceń otrzymamy ciąg postaci , Gdzieλ jest liczbą różną od zera, to układ jest niespójny (nie ma rozwiązań).

Jak zapisać zakończenie zadania? Musisz zapisać zdanie:

„W wyniku elementarnych przekształceń otrzymano ciąg znaków w postaci gdzie λ ≠ 0 " Odpowiedź: „Układ nie ma rozwiązań (niespójny).”

Należy pamiętać, że w tym przypadku nie ma odwrócenia algorytmu Gaussa, nie ma rozwiązań i po prostu nie ma czego szukać.

Przykład 2

Rozwiązać układ równań liniowych

To jest przykład, który możesz rozwiązać samodzielnie. Pełne rozwiązanie i odpowiedź na końcu lekcji.

Przypominamy jeszcze raz, że Twoje rozwiązanie może różnić się od naszego, metoda Gaussa nie określa jednoznacznego algorytmu, a same działania należy odgadnąć w każdym przypadku niezależnie.

Kolejna cecha techniczna rozwiązania: można zatrzymać przekształcenia elementarne natychmiast, jak tylko pojawi się linia typu , gdzie λ ≠ 0 . Rozważmy przykład warunkowy: załóżmy, że po pierwszej transformacji otrzymana zostanie macierz

.

Macierz ta nie została jeszcze zredukowana do postaci schodkowej, ale nie ma już potrzeby dalszych elementarnych przekształceń, gdyż pojawiła się linia postaci, gdzie λ ≠ 0 . Należy od razu odpowiedzieć, że system jest niekompatybilny.

Kiedy układ równań liniowych nie ma rozwiązań, jest niemal prezentem dla ucznia, ponieważ uzyskuje się krótkie rozwiązanie, czasem dosłownie w 2-3 krokach. Ale wszystko na tym świecie jest zrównoważone, a problem, w którym układ ma nieskończenie wiele rozwiązań, jest po prostu dłuższy.

Przykład 3:

Rozwiązać układ równań liniowych

Istnieją 4 równania i 4 niewiadome, więc układ może mieć jedno rozwiązanie, nie mieć rozwiązań, lub mieć nieskończenie wiele rozwiązań. Tak czy inaczej, metoda Gaussa w każdym razie doprowadzi nas do odpowiedzi. Na tym polega jego wszechstronność.

Początek znowu standardowy. Zapiszmy rozszerzoną macierz układu i za pomocą elementarnych przekształceń sprowadźmy ją do postaci krokowej:

To wszystko, a ty się bałeś.

(1). Należy pamiętać, że wszystkie liczby w pierwszej kolumnie są podzielne przez 2, więc 2 będzie w porządku w lewym górnym kroku. Do drugiej linii dodajemy pierwszą linię pomnożoną przez (–4). Do trzeciej linii dodajemy pierwszą linię pomnożoną przez (–2). Do czwartej linii dodajemy pierwszą linię pomnożoną przez (–1).

Uwaga! Wielu może skusić czwarta linijka odejmować pierwsza linia. Można to zrobić, ale nie jest to konieczne; doświadczenie pokazuje, że prawdopodobieństwo błędu w obliczeniach wzrasta kilkakrotnie. Po prostu dodajemy: do czwartej linii dodajemy pierwszą linię pomnożoną przez (–1) – dokładnie tak!

(2). Ostatnie trzy linie są proporcjonalne, dwie z nich można usunąć. Tutaj znowu musimy się pokazać zwiększona uwaga, ale czy linie są rzeczywiście proporcjonalne? Dla pewności dobrym pomysłem byłoby pomnożenie drugiej linii przez (–1) i podzielenie czwartej linii przez 2, w wyniku czego otrzymamy trzy identyczne linie. I dopiero potem usuń dwa z nich. W wyniku elementarnych przekształceń rozszerzona macierz układu sprowadza się do postaci krokowej:

Pisząc zadanie w zeszycie, zaleca się robienie tych samych notatek ołówkiem dla przejrzystości.

Przepiszmy odpowiedni układ równań:

Nie ma tu zapachu „zwykłego” pojedynczego rozwiązania systemu. Zła linia gdzie λ ≠ 0, też nie. Oznacza to, że jest to trzeci pozostały przypadek – układ ma nieskończenie wiele rozwiązań.

Nieskończony zbiór rozwiązań układu zapisuje się w skrócie w postaci tzw ogólne rozwiązanie układu.

Rozwiązanie ogólne układu znajdujemy za pomocą odwrotności metody Gaussa. W przypadku układów równań o nieskończonym zbiorze rozwiązań pojawiają się nowe pojęcia: „podstawowe zmienne” I „darmowe zmienne”. Najpierw zdefiniujmy, jakie mamy zmienne podstawowy i które zmienne - bezpłatny. Nie trzeba szczegółowo wyjaśniać pojęć algebry liniowej; wystarczy pamiętać, że takie istnieją podstawowe zmienne I wolne zmienne.

Zmienne podstawowe zawsze „siedzą” ściśle na stopniach macierzy. W tym przykładzie podstawowymi zmiennymi są X 1 i X 3 .

Wolne zmienne są wszystkim pozostały zmienne, które nie otrzymały kroku. W naszym przypadku są dwa z nich: X 2 i X 4 – zmienne wolne.

Teraz potrzebujesz Wszystkopodstawowe zmienne wyrazić tylko przezwolne zmienne. Odwrotność algorytmu Gaussa tradycyjnie działa od dołu do góry. Z drugiego równania układu wyrażamy zmienną podstawową X 3:

Spójrzmy teraz na pierwsze równanie: . Najpierw podstawiamy do niego znalezione wyrażenie:

Pozostaje wyrazić zmienną podstawową X 1 poprzez wolne zmienne X 2 i X 4:

W końcu mamy to, czego potrzebowaliśmy – Wszystko podstawowe zmienne ( X 1 i X 3) wyrażone tylko przez wolne zmienne ( X 2 i X 4):

Właściwie ogólne rozwiązanie jest gotowe:

.

Jak poprawnie napisać rozwiązanie ogólne? Po pierwsze, zmienne wolne wpisuje się do rozwiązania ogólnego „same” i ściśle na swoich miejscach. W tym przypadku zmienne wolne X 2 i X 4 należy wpisać na drugim i czwartym miejscu:

.

Wynikowe wyrażenia dla podstawowych zmiennych i oczywiście należy zapisać na pierwszej i trzeciej pozycji:

Z ogólnego rozwiązania układu można znaleźć nieskończenie wiele rozwiązania prywatne. To bardzo proste. Dowolne zmienne X 2 i X 4 są tak nazywane, ponieważ można je dać jakiekolwiek wartości końcowe. Najpopularniejszymi wartościami są wartości zerowe, ponieważ jest to najłatwiejsze do uzyskania rozwiązanie częściowe.

Zastępowanie ( X 2 = 0; X 4 = 0) do rozwiązania ogólnego otrzymujemy jedno z rozwiązań szczegółowych:

, lub jest konkretnym rozwiązaniem odpowiadającym wolnym zmiennym o wartościach ( X 2 = 0; X 4 = 0).

Kolejną słodką parą są jedynki, zamieńmy ( X 2 = 1 i X 4 = 1) do rozwiązania ogólnego:

, czyli (-1; 1; 1; 1) – kolejne szczególne rozwiązanie.

Łatwo zobaczyć, że układ równań ma nieskończenie wiele rozwiązań ponieważ możemy podać darmowe zmienne każdy znaczenia.

Każdy dane rozwiązanie musi spełniać każdemu równanie układu. Jest to podstawa do „szybkiego” sprawdzenia poprawności rozwiązania. Weźmy na przykład konkretne rozwiązanie (-1; 1; 1; 1) i podstawmy je po lewej stronie każdego równania układu pierwotnego:

Wszystko musi się zgadzać. W przypadku każdego konkretnego rozwiązania, które otrzymasz, wszystko powinno się zgadzać.

Ściślej rzecz ujmując, sprawdzanie konkretnego rozwiązania czasem oszukuje, tzn. jakieś szczególne rozwiązanie może spełniać każde równanie układu, ale samo rozwiązanie ogólne jest w rzeczywistości znajdowane niepoprawnie. Dlatego przede wszystkim weryfikacja rozwiązania ogólnego jest dokładniejsza i bardziej wiarygodna.

Jak sprawdzić wynikowe rozwiązanie ogólne ?

Nie jest to trudne, ale wymaga długotrwałych przekształceń. Musimy przyjąć wyrażenia podstawowy w tym przypadku zmienne i , i podstaw je po lewej stronie każdego równania układu.

Po lewej stronie pierwszego równania układu:

Otrzymuje się prawą stronę początkowego pierwszego równania układu.

Po lewej stronie drugiego równania układu:

Otrzymuje się prawą stronę początkowego drugiego równania układu.

A potem - po lewej stronie trzeciego i czwartego równania układu. Ta kontrola trwa dłużej, ale gwarantuje 100% poprawność całego rozwiązania. Dodatkowo niektóre zadania wymagają sprawdzenia rozwiązania ogólnego.

Przykład 4:

Rozwiązać układ metodą Gaussa. Znajdź rozwiązanie ogólne i dwa szczegółowe. Sprawdź rozwiązanie ogólne.

To jest przykład, który możesz rozwiązać samodzielnie. Tutaj, nawiasem mówiąc, znowu liczba równań jest mniejsza niż liczba niewiadomych, co oznacza od razu jasne, że układ będzie albo niespójny, albo będzie miał nieskończoną liczbę rozwiązań.

Przykład 5:

Rozwiązać układ równań liniowych. Jeżeli układ ma nieskończenie wiele rozwiązań, znajdź dwa rozwiązania szczególne i sprawdź rozwiązanie ogólne

Rozwiązanie: Zapiszmy rozszerzoną macierz układu i za pomocą elementarnych przekształceń sprowadźmy ją do postaci krokowej:

(1). Dodaj pierwszą linię do drugiej linii. Do trzeciej linii dodajemy pierwszą linię pomnożoną przez 2. Do czwartej linii dodajemy pierwszą linię pomnożoną przez 3.

(2). Do trzeciej linii dodajemy drugą linię pomnożoną przez (–5). Do czwartej linii dodajemy drugą linię pomnożoną przez (–7).

(3). Trzecia i czwarta linia są takie same, usuwamy jedną z nich. To taka piękność:

Na stopniach znajdują się zmienne podstawowe, zatem - zmienne podstawowe.

Jest tylko jedna wolna zmienna, która nie dostała tutaj kroku: .

(4). Ruch odwrotny. Wyraźmy podstawowe zmienne poprzez zmienną wolną:

Z trzeciego równania:

Rozważmy drugie równanie i podstawmy do niego znalezione wyrażenie:

, , ,

Rozważmy pierwsze równanie i podstawmy znalezione wyrażenia i do niego:

Zatem rozwiązanie ogólne z jedną zmienną wolną X 4:

Jeszcze raz, jak to się skończyło? Dowolna zmienna X 4 zajmuje samotnie należne mu czwarte miejsce. Powstałe wyrażenia dla podstawowych zmiennych , , są również na swoim miejscu.

Sprawdźmy od razu rozwiązanie ogólne.

Podstawiamy zmienne podstawowe , , po lewej stronie każdego równania układu:

Otrzymuje się odpowiednie prawe strony równań, w ten sposób znajduje się prawidłowe rozwiązanie ogólne.

Teraz ze znalezionego ogólnego rozwiązania otrzymujemy dwa konkretne rozwiązania. Wszystkie zmienne są tutaj wyrażone poprzez wartość pojedynczą wolna zmienna x 4. Nie ma potrzeby zawracać sobie głowy.

Pozwalać X 4 = 0 w takim razie – pierwsze konkretne rozwiązanie.

Pozwalać X Zatem 4 = 1 – kolejne rozwiązanie prywatne.

Odpowiedź: Ogólne rozwiązanie: . Rozwiązania prywatne:

I .

Przykład 6:

Znajdź rozwiązanie ogólne układu równań liniowych.

Sprawdziliśmy już ogólne rozwiązanie; odpowiedzi można zaufać. Twoje rozwiązanie może różnić się od naszego. Najważniejsze, że ogólne decyzje są zbieżne. Prawdopodobnie wiele osób zauważyło nieprzyjemny moment w rozwiązaniach: bardzo często podczas odwrotnego przebiegu metody Gaussa musieliśmy majstrować przy zwykłych ułamkach. W praktyce rzeczywiście tak jest; przypadki, w których nie ma ułamków, są znacznie mniej powszechne. Bądź przygotowany mentalnie i, co najważniejsze, technicznie.

Zastanówmy się nad cechami rozwiązania, których nie znaleziono w rozwiązanych przykładach. Ogólne rozwiązanie układu może czasami zawierać stałą (lub stałe).

Na przykład rozwiązanie ogólne: . Tutaj jedna z podstawowych zmiennych jest równa liczbie stałej: . Nie ma w tym nic egzotycznego, zdarza się. Oczywiście w tym przypadku każde konkretne rozwiązanie będzie zawierało piątkę na pierwszej pozycji.

Rzadko, ale są systemy, w których liczba równań jest większa niż liczba zmiennych. Metoda Gaussa sprawdza się jednak w najcięższych warunkach. Należy na spokojnie sprowadzić rozszerzoną macierz układu do postaci krokowej stosując standardowy algorytm. Taki system może być niespójny, może mieć nieskończenie wiele rozwiązań i, co dziwne, może mieć jedno rozwiązanie.

Powtórzmy naszą radę – aby czuć się komfortowo przy rozwiązywaniu układu metodą Gaussa, należy być dobrym w rozwiązywaniu przynajmniej kilkunastu układów.

Rozwiązania i odpowiedzi:

Przykład 2:

Rozwiązanie:Zapiszmy rozszerzoną macierz układu i za pomocą elementarnych przekształceń sprowadźmy ją do postaci krokowej.

Wykonane przekształcenia elementarne:

(1) Pierwsza i trzecia linia zostały zamienione miejscami.

(2) Pierwsza linia została dodana do drugiej linii, pomnożona przez (–6). Pierwsza linia została dodana do trzeciej linii, pomnożona przez (–7).

(3) Druga linia została dodana do trzeciej linii, pomnożona przez (–1).

W wyniku elementarnych przekształceń otrzymujemy ciąg znaków, Gdzie λ ≠ 0 .Oznacza to, że system jest niespójny.Odpowiedź: nie ma rozwiązań.

Przykład 4:

Rozwiązanie:Zapiszmy rozszerzoną macierz układu i za pomocą elementarnych przekształceń sprowadźmy ją do postaci krokowej:

Wykonane konwersje:

(1). Pierwsza linia pomnożona przez 2 została dodana do drugiej linii. Pierwsza linia pomnożona przez 3 została dodana do trzeciej linii.

Nie ma jednostki dla drugiego etapu , a transformacja (2) ma na celu jego uzyskanie.

(2). Trzecia linia została dodana do drugiej linii, pomnożona przez –3.

(3). Druga i trzecia linia zostały zamienione miejscami (wynikowe –1 przenieśliśmy do drugiego kroku)

(4). Trzecia linia została dodana do drugiej linii, pomnożona przez 3.

(5). W pierwszych dwóch wierszach zmieniono znak (pomnożono przez –1), w trzecim podzielono przez 14.

Odwracać:

(1). Tutaj to podstawowe zmienne (które znajdują się na schodach), oraz – zmienne wolne (które nie dostały kroku).

(2). Wyraźmy podstawowe zmienne w kategoriach zmiennych wolnych:

Z trzeciego równania: .

(3). Rozważmy drugie równanie:, rozwiązania prywatne:

Odpowiedź: Ogólne rozwiązanie:

Liczby zespolone

W tej części przedstawimy to pojęcie liczba zespolona, rozważać algebraiczny, trygonometryczny I forma wykładnicza liczba zespolona. Dowiemy się również, jak wykonywać operacje na liczbach zespolonych: dodawanie, odejmowanie, mnożenie, dzielenie, potęgowanie i wyciąganie pierwiastka.

Aby opanować liczby zespolone, nie jest wymagana żadna specjalna wiedza z wyższego kursu matematyki, a materiał jest dostępny nawet dla uczniów. Wystarczy umieć wykonywać operacje algebraiczne na „zwykłych” liczbach i pamiętać o trygonometrii.

Na początek pamiętajmy o „zwykłych” liczbach. W matematyce są to tzw zbiór liczb rzeczywistych i są oznaczone literą R, lub R (pogrubiony). Wszystkie liczby rzeczywiste leżą na znanej osi liczbowej:

Towarzystwo liczb rzeczywistych jest bardzo różnorodne - występują tutaj liczby całkowite, ułamki zwykłe i liczby niewymierne. W tym przypadku każdy punkt na osi liczbowej koniecznie odpowiada jakiejś liczbie rzeczywistej.