Konstrukcja przekrojów wielościanu na przykładzie pryzmatu. Lekcja praktyczna: „Konstrukcja odcinków równoległościanu”

Cele lekcji: rozważ rozwiązanie problemów związanych z konstruowaniem przekrojów, jeśli dwa punkty przekroju należą do tej samej ściany.

Postęp lekcji

Nauka nowych koncepcji
Definicja 1. Płaszczyzną przecięcia wielościanu jest dowolna płaszczyzna, po obu stronach której znajdują się punkty danego wielościanu.
Definicja 2. Przekrój wielościanu to wielokąt, którego boki są odcinkami, wzdłuż których płaszczyzna cięcia przecina ściany wielościanu.
Ćwiczenia. Nazwij odcinki, wzdłuż których płaszczyzna cięcia przecina ściany równoległościanu (ryc. 1). Nazwij przekrój równoległościanu.

Podstawowe czynności podczas konstruowania przekrojów

	Podstawa teoretyczna	Odpowiedź
1. Jak sprawdzić, czy odcinek został zbudowany, czy nie	Definicja sekcji	Musi to być wielokąt, którego boki należą do ścian wielościanu
2. Przed przystąpieniem do pracy należy ustalić, czy na podstawie danych zadania możliwe jest zbudowanie przekroju	Metody definiowania płaszczyzny	Jest to możliwe, jeśli elementy te jednoznacznie definiują płaszczyznę, czyli podane są trzy punkty nie leżące na tej samej prostej, punkt i prosta itp.
3. W płaszczyźnie jakiejś ściany znajdują się dwa punkty płaszczyzny cięcia	Jeśli dwa punkty należą do płaszczyzny, to cała linia należy do płaszczyzny	Narysuj linię prostą przechodzącą przez te punkty
4. W jednej z równoległych ścian znajduje się bok przekroju, a w drugiej punkt przekroju	Własność płaszczyzn równoległych	Przez ten punkt poprowadź linię równoległą do tego punktu
5. Na jednej ścianie znajduje się punkt przekroju i wiadomo, że płaszczyzna cięcia przechodzi przez linię równoległą do tej ściany	Znak równoległości linii i płaszczyzny. Własność płaszczyzn równoległych	Skonstruuj linię przecięcia płaszczyzn równoległych do danej prostej
6. Dwa punkty przekroju należą do jednej ściany, a trzeci punkt leży w sąsiedniej	Aksjomaty stereometrii	Płaszczyzna cięcia przecina ściany wzdłuż odcinków OC i AB, które nazywane są śladem płaszczyzny cięcia na ścianach

Rozwiązywanie problemów

Zadanie 1. Który z czworokątów EFKM czy EFKL może być przekrojem tego wielościanu (rys. 2)? Dlaczego?

Zadanie 2. Student narysował przekrój czworościanu (ryc. 3). Czy taki odcinek jest możliwy?

Rozwiązanie. Należy udowodnić, że N, M i H, L leżą w tej samej płaszczyźnie. Niech punkty N i M należą do ściany tylnej, H i L do ściany dolnej, czyli punkt przecięcia NM i HL musi leżeć na prostej należącej do obu ścian, czyli AC. Przedłużmy linie NM i HL i znajdźmy punkt ich przecięcia. Punkt ten nie będzie należał do prostej AC. Oznacza to, że punkty N, M, L, H nie tworzą płaskiego wielokąta. Niemożliwe.

Zadanie 3. Skonstruuj odcinek czworościanu ABCS z płaszczyzną przechodzącą przez punkty K, L, N, gdzie K i N są środkami odpowiednio krawędzi SA i SB (rys. 4).

1. W jakim licu można wykonać boki przekroju?

2. Wybierz jeden z punktów, w których przekrój zostanie przerwany.
Rozwiązanie. Metoda I. Wybierz punkt L.
Określamy ścianę, w której leży wybrany punkt i w której konieczne jest zbudowanie przekroju.

Wyznaczamy ścianę, w której leży prosta KN, nie przechodząca przez wybrany punkt L.

Znajdź linię przecięcia ścian ABC i ASB.

Jakie jest względne położenie prostych KN i AB (ryc. 5)?
[Równoległy.]

Co należy skonstruować, jeśli płaszczyzna cięcia przechodzi przez linię prostą równoległą do linii przecięcia płaszczyzn?
[Narysuj linię równoległą do AB przechodzącą przez punkt L. Linia ta przecina krawędź CB w punkcie P.]
Łączymy punkty należące do tej samej ściany. KLPN - wymagana sekcja.
Metoda II. Wybierz punkt N (rys. 6).

Wyznaczamy ściany, w których leży punkt N i prosta KL.

Linia przecięcia tych płaszczyzn będzie linią prostą SC. Znajdź punkt przecięcia linii KL i SC. Oznaczmy to Y.
Połącz punkty N i Y. Linia NY przecina krawędź CB w punkcie P.
Łączymy punkty należące do tej samej ściany.
KLNP - wymagana sekcja.
Wyjaśnij tę decyzję.
Jeden uczeń pracuje przy tablicy, reszta w zeszytach.

Problem 4. Zbuduj odcinek równoległościanu przechodzący przez punkty M, P i H, H ` (A1B1C1) (ryc. 7).

Rozwiązanie. 1. Połącz punkty należące do tej samej ściany.
2. Którą linię i punkt wybierzemy do skonstruowania przekroju?
3. Co dalej ustalamy?
4. Jakie jest względne położenie wybranej prostej i linii przecięcia ścian (ryc. 8)?

5. Jak skonstruować ślad płaszczyzny cięcia na ścianie B1C1D1A1 przechodzącej przez punkt H?
6. Połącz punkty należące do tej samej ściany.
7. Jaką linię i punkt wybrać do skonstruowania śladu płaszczyzny cięcia na ścianie AA1D1D?
8. Jakie jest względne położenie ścian BB1C1C i AA1D1D?
9. Z jakiej własności należy skorzystać, aby skonstruować ślad płaszczyzny cięcia na ścianie AA1D1D?
10. Nazwij wymaganą sekcję.

Zadanie 5. Zbuduj odcinek piramidy SABCD przechodzący przez punkty M, P i H,
H` (ABC) (ryc. 9).

Odpowiedź: Patrz rysunek 10.

Zadanie domowe

Zadanie. Jak zmienią się konstrukcje jeśli dokładnie
Jak H zmieni swoje położenie? Konstruuj sekcje, korzystając z różnych opcji (ryc. 11).

Dzisiaj ponownie przyjrzymy się, jak to zrobić skonstruuj odcinek czworościanu z płaszczyzną.
Rozważmy najprostszy przypadek (poziom obowiązkowy), gdy 2 punkty płaszczyzny przekroju należą do jednej ściany, a trzeci punkt należy do drugiej ściany.

Przypomnijmy algorytm konstruowania przekrojów tego typu (przypadek: 2 punkty należą do tej samej ściany).

1. Szukamy ściany zawierającej 2 punkty płaszczyzny przekroju. Narysuj linię prostą przechodzącą przez dwa punkty leżące na tej samej ścianie. Znajdujemy punkty jego przecięcia z krawędziami czworościanu. Część linii prostej kończąca się na powierzchni to bok przekroju.

2. Jeśli wielokąt można zamknąć, oznacza to, że przekrój został skonstruowany. Jeśli zamknięcie nie jest możliwe, znajdujemy punkt przecięcia skonstruowanej linii i płaszczyzny zawierającej trzeci punkt.

1. Widzimy, że punkty E i F leżą na tej samej ścianie (BCD), narysuj linię prostą EF na płaszczyźnie (BCD).
2. Znajdźmy punkt przecięcia prostej EF z krawędzią czworościanu BD, jest to punkt H.
3. Teraz musisz znaleźć punkt przecięcia prostej EF i płaszczyzny zawierającej trzeci punkt G, tj. płaszczyzna (ADC).
Prosta CD leży w płaszczyznach (ADC) i (BDC), co oznacza, że ​​przecina prostą EF, a punkt K jest punktem przecięcia prostej EF i płaszczyzny (ADC).
4. Następnie znajdujemy jeszcze dwa punkty leżące w tej samej płaszczyźnie. Są to punkty G i K, oba leżą w płaszczyźnie lewej ściany bocznej. Rysujemy linię GK i zaznaczamy punkty, w których linia ta przecina krawędzie czworościanu. Są to punkty M i L.
4. Pozostaje „zamknąć” sekcję, czyli połączyć punkty leżące na tej samej powierzchni. Są to punkty M i H, a także L i F. Obydwa te odcinki są niewidoczne, rysujemy je linią przerywaną.

Przekrój okazał się czworokątem MHFL. Wszystkie jego wierzchołki leżą na krawędziach czworościanu. Wybierzmy wynikową sekcję.

Teraz sformułujmy „właściwości” poprawnie skonstruowanej sekcji:

1. Wszystkie wierzchołki wielokąta będącego przekrojem leżą na krawędziach czworościanu (równoległościanu, wielokąta).

2. Wszystkie boki przekroju leżą na ścianach wielościanu.
3. Każda ściana wielokąta może zawierać nie więcej niż jeden (jeden lub żaden!) bok przekroju

Na tej lekcji przyjrzymy się czworościanowi i jego elementom (krawędź czworościanu, powierzchnia, ściany, wierzchołki). Rozwiążemy kilka problemów związanych z konstruowaniem przekrojów czworościanu, stosując ogólną metodę konstruowania przekrojów.

Temat: Równoległość linii i płaszczyzn

Lekcja: czworościan. Zagadnienia konstruowania przekrojów czworościanu

Jak zbudować czworościan? Weźmy dowolny trójkąt ABC. Dowolny punkt D, nie leżącego w płaszczyźnie tego trójkąta. Otrzymujemy 4 trójkąty. Powierzchnia utworzona przez te 4 trójkąty nazywana jest czworościanem (ryc. 1.). Wewnętrzne punkty ograniczone tą powierzchnią są również częścią czworościanu.

Ryż. 1. Czworościan ABCD

Elementy czworościanu
A,B, C, D - wierzchołki czworościanu.
AB, AC, OGŁOSZENIE, przed Chrystusem, BD, płyta CD - krawędzie czworościanu.
ABC, ABD, BDC, ADC - twarze czworościanu.

Komentarz: można brać na płasko ABC Do podstawa czworościanu, a następnie wskaż D Jest wierzchołek czworościanu. Każda krawędź czworościanu jest przecięciem dwóch płaszczyzn. Na przykład żebro AB- to jest przecięcie płaszczyzn ABD I ABC. Każdy wierzchołek czworościanu jest przecięciem trzech płaszczyzn. Wierzchołek A leży w płaszczyznach ABC, ABD, ADZ. Kropka A jest przecięciem trzech wyznaczonych płaszczyzn. Fakt ten zapisano w następujący sposób: A= ABC ∩ ABD ∩ ACD.

Definicja czworościanu

Więc, tetraedr to powierzchnia utworzona przez cztery trójkąty.

Krawędź czworościanu- linia przecięcia dwóch płaszczyzn czworościanu.

Z 6 zapałek utwórz 4 równe trójkąty. Nie da się rozwiązać problemu w samolocie. A jest to łatwe do zrobienia w kosmosie. Weźmy czworościan. 6 zapałek to jego krawędzie, cztery ściany czworościanu i będą cztery równe trójkąty. Problem został rozwiązany.

Biorąc pod uwagę czworościan ABCD. Kropka M należy do krawędzi czworościanu AB, punkt N należy do krawędzi czworościanu WD i okres R należy do krawędzi DZ(ryc. 2.). Skonstruuj odcinek czworościanu z płaszczyzną MNP.

Ryż. 2. Rysunek do zadania 2 - Skonstruuj odcinek czworościanu z płaszczyzną

Rozwiązanie:
Rozważmy ścianę czworościanu DSłoneczny. Z tej strony N I P należą do twarzy DSłoneczny, a zatem czworościan. Ale zgodnie z warunkiem punktu N., P należą do płaszczyzny cięcia. Oznacza, NP- jest to linia przecięcia dwóch płaszczyzn: płaszczyzna twarzy DSłoneczny i płaszczyzna cięcia. Załóżmy, że linie proste NP I Słoneczny nie równolegle. Leżą w tej samej płaszczyźnie DSłoneczny. Znajdźmy punkt przecięcia linii NP I Słoneczny. Oznaczmy to mi(ryc. 3.).

Ryż. 3. Rysunek problemu 2. Znalezienie punktu E

Kropka mi należy do płaszczyzny przekroju MNP, ponieważ leży na prostej NP i linię prostą NP leży całkowicie w płaszczyźnie przekroju MNP.

Wskaż także mi leży w samolocie ABC, ponieważ leży na prostej Słoneczny z samolotu ABC.

Rozumiemy to EM- linia przecięcia płaszczyzn ABC I MNP, od punktów mi I M leżą jednocześnie w dwóch płaszczyznach - ABC I MNP. Połączmy kropki M I mi i jedź dalej prosto EM do przecięcia z linią AC. Punkt przecięcia linii EM I AC oznaczmy Q.

Więc w tym przypadku NPQМ- wymagana sekcja.

Ryż. 4. Rysunek problemu 2. Rozwiązanie problemu 2

Rozważmy teraz przypadek, kiedy NP równoległy przed Chrystusem. Jeśli prosto NP równolegle do jakiejś linii, na przykład linii prostej Słoneczny z samolotu ABC, potem prosto NP równolegle do całej płaszczyzny ABC.

Żądana płaszczyzna przekroju przechodzi przez linię prostą NP, równolegle do płaszczyzny ABC, i przecina płaszczyznę po linii prostej MQ. Zatem linia przecięcia MQ równolegle do linii NP. Dostajemy NPQМ- wymagana sekcja.

Kropka M leży na bocznej krawędzi ADW tetraedr ABCD. Skonstruuj odcinek czworościanu z płaszczyzną przechodzącą przez ten punkt M równolegle do podstawy ABC.

Ryż. 5. Rysunek do zadania 3 Skonstruuj przekrój czworościanu z płaszczyzną

Rozwiązanie:
Płaszczyzna cięcia φ równolegle do płaszczyzny ABC zgodnie z warunkiem oznacza to, że ten samolot φ równolegle do linii AB, AC, Słoneczny.
W samolocie ABD przez punkt M zróbmy bezpośredni PQ równoległy AB(ryc. 5). Prosty PQ leży w samolocie ABD. Podobnie w samolocie ACD przez punkt R zróbmy bezpośredni PR równoległy AC. Mam rację R. Dwie przecinające się linie PQ I PR samolot PQR odpowiednio równoległe do dwóch przecinających się linii AB I AC samolot ABC, czyli samoloty ABC I PQR równoległy. PQR- wymagana sekcja. Problem został rozwiązany.

Biorąc pod uwagę czworościan ABCD. Kropka M- punkt wewnętrzny, punkt na ścianie czworościanu ABD. N- punkt wewnętrzny odcinka DZ(ryc. 6.). Skonstruuj punkt przecięcia linii N.M. i samoloty ABC.

Ryż. 6. Rysunek do zadania 4

Rozwiązanie:
Aby rozwiązać ten problem, zbudujemy płaszczyznę pomocniczą DMN. Niech będzie prosto DM przecina w punkcie prostą AB DO(ryc. 7.). Następnie, SKD- to jest fragment samolotu DMN i czworościan. W samolocie DMN kłamstwa i prosto N.M. i wynikową linię prostą SK. Więc jeśli N.M. nie równolegle SK, to w pewnym momencie się przetną R. Kropka R i pojawi się pożądany punkt przecięcia linii N.M. i samoloty ABC.

Ryż. 7. Rysunek problemu 4. Rozwiązanie problemu 4

Biorąc pod uwagę czworościan ABCD. M- wewnętrzny punkt twarzy ABD. R- wewnętrzny punkt twarzy ABC. N- punkt wewnętrzny krawędzi DZ(ryc. 8.). Skonstruuj odcinek czworościanu z płaszczyzną przechodzącą przez punkty M, N I R.

Ryż. 8. Rysunek do zadania 5 Skonstruuj przekrój czworościanu z płaszczyzną

Rozwiązanie:
Rozważmy pierwszy przypadek, gdy linia prosta MN nie jest równoległy do ​​płaszczyzny ABC. W poprzednim zadaniu znaleźliśmy punkt przecięcia prostej MN i samoloty ABC. O to właśnie chodzi DO, uzyskuje się to za pomocą płaszczyzny pomocniczej DMN, tj. prowadzimy DM i mamy punkt F. Wykonujemy CF i na skrzyżowaniu MN zdobywamy punkt DO.

Ryż. 9. Rysunek problemu 5. Znalezienie punktu K

Zróbmy bezpośredni KR. Prosty KR leży zarówno w płaszczyźnie przekroju, jak i w płaszczyźnie ABC. Zdobycie punktów P 1 I R2. Złączony P 1 I M i jako kontynuacja rozumiemy sedno M 1. Łączenie kropki R2 I N. W rezultacie otrzymujemy pożądaną sekcję P 1 P 2 NM 1. W pierwszym przypadku problem został rozwiązany.
Rozważmy drugi przypadek, gdy linia prosta MN równolegle do płaszczyzny ABC. Samolot MNP przechodzi przez linię prostą MN równolegle do płaszczyzny ABC i przecina płaszczyznę ABC wzdłuż jakiejś linii prostej R 1 R 2, potem prosto R 1 R 2 równolegle do danej linii MN(ryc. 10.).

Ryż. 10. Rysunek do zadania 5. Wymagana sekcja

Teraz narysujmy linię prostą R1 M i mamy punkt M 1.P 1 P 2 NM 1- wymagana sekcja.

Przyjrzeliśmy się więc czworościanowi i rozwiązaliśmy kilka typowych problemów z czworościanem. W następnej lekcji przyjrzymy się równoległościanowi.

1. I. M. Smirnova, V. A. Smirnov. - wydanie V, poprawione i rozszerzone - M.: Mnemosyne, 2008. - 288 s. : chory. Geometria. Klasy 10-11: podręcznik dla uczniów szkół ogólnokształcących (poziom podstawowy i specjalizowany)

2. Sharygin I.F. - M.: Drop, 1999. - 208 s.: chory. Geometria. Klasy 10-11: Podręcznik dla placówek kształcenia ogólnego

3. E. V. Potoskuev, L. I. Zvalich. - Wydanie 6, stereotyp. - M.: Drop, 008. - 233 s. :il. Geometria. Klasa 10: Podręcznik dla placówek kształcenia ogólnego obejmujący pogłębioną i specjalistyczną naukę matematyki

Dodatkowe zasoby internetowe

2. Jak skonstruować przekrój czworościanu. Matematyka ().

3. Festiwal idei pedagogicznych ().

Rozwiązuj w domu zadania na temat „Czworościan”, jak znaleźć krawędź czworościanu, ściany czworościanu, wierzchołki i powierzchnię czworościanu

1. Geometria. Klasy 10-11: podręcznik dla uczniów szkół ogólnokształcących (poziom podstawowy i specjalistyczny) I. M. Smirnova, V. A. Smirnov. - wydanie V, poprawione i rozszerzone - M.: Mnemosyne, 2008. - 288 s.: il. Zadania 18, 19, 20 s. 50

2. Punkt miżyłka MAMA tetraedr MAVS. Skonstruuj odcinek czworościanu z płaszczyzną przechodzącą przez punkty B, C I mi.

3. W czworościanie MABC punkt M należy do ściany AMV, punkt P należy do ściany BMC, punkt K należy do krawędzi AC. Skonstruuj odcinek czworościanu z płaszczyzną przechodzącą przez punkty M, R, K.

4. Jakie kształty można uzyskać w wyniku przecięcia czworościanu z płaszczyzną?

Aksjomaty planimetrii:

W różnych podręcznikach właściwości linii i płaszczyzn można przedstawić na różne sposoby, w formie aksjomatu, wniosku z niego, twierdzenia, lematu itp. Rozważ podręcznik Pogorełowa A.V.

Linia prosta dzieli płaszczyznę na dwie półpłaszczyzny.

0

Z dowolnej półprostej można wykreślić kąt o danej mierze mniejszej niż 180 stopni w daną półpłaszczyznę. 0 i tylko jeden.

Czymkolwiek jest trójkąt, w danym miejscu względem danej półprostej znajduje się trójkąt równy.

Przez punkt nie leżący na danej prostej można poprowadzić na płaszczyźnie co najwyżej jedną prostą równoległą do danej.

Aksjomaty stereometrii:

Jakakolwiek jest płaszczyzna, istnieją punkty, które do tej płaszczyzny należą, i punkty, które do tej płaszczyzny nie należą, i punkty, które do niej nie należą.

Jeżeli dwie różne płaszczyzny mają wspólny punkt, to przecinają się one wzdłuż linii prostej przechodzącej przez ten punkt.

Jeśli dwie różne linie mają wspólny punkt, wówczas można przez nie poprowadzić płaszczyznę i tylko jedną.

Niezależnie od linii, istnieją punkty należące do tej linii i punkty, które do niej nie należą.

Przez dowolne dwa punkty można narysować linię prostą i tylko jedną.

Z trzech punktów na linii jeden i tylko jeden leży pomiędzy dwoma pozostałymi.

Każdy segment ma pewną długość większą od zera. Długość odcinka jest równa sumie długości części, na które jest on podzielony przez dowolny z jego punktów.

Linia prosta należąca do płaszczyzny dzieli tę płaszczyznę na dwie półpłaszczyzny.

Każdy kąt ma miarę stopnia większą od zera. Kąt prosty ma miarę 180 0 . Miara stopnia kąta jest równa sumie miar stopnia kątów, na które jest on podzielony przez dowolny promień przechodzący między jego bokami.

Na dowolnej półprostej od jej punktu początkowego można wykreślić odcinek o danej długości i tylko jeden.

Z półprostej płaszczyzny ją zawierającej można wykreślić kąt o danej mierze mniejszej niż 180 stopni w daną półpłaszczyznę 0 i tylko jeden.

Niezależnie od trójkąta, w danej płaszczyźnie i w danym miejscu znajduje się równy trójkąt względem danej półprostej tej płaszczyzny.

Na płaszczyźnie, przez dany punkt nie leżący na danej prostej, można poprowadzić co najwyżej jedną prostą równoległą do danej.

Sekcja

W przestrzeni dwie figury, w naszym przypadku płaszczyzna i wielościan, mogą mieć następujące względne położenie: nie przecinają się, przecinają się w punkcie, przecinają się po linii prostej oraz płaszczyzna przecina wielościan wzdłuż jego wnętrza (ryc. 1) , a jednocześnie tworzą następujące liczby:

a) pusta figura (nie przecinają się)

b) punkt

c) segment

d) wielokąt

Jeśli na przecięciu wielościanu i płaszczyzny znajduje się wielokąt, to jest to wielokątnazywany odcinkiem wielościanu z płaszczyzną .

Ryc.1

Definicja. Sekcja ciało przestrzenne (np. wielościan) to figura wynikająca z przecięcia bryły z płaszczyzną.

Płaszczyzna cięcia wielościan nazwijmy dowolną płaszczyznę, po obu stronach której znajdują się punkty danego wielościanu.

Rozważymy tylko przypadek, gdy płaszczyzna przecina wielościan wzdłuż jego wnętrza. W tym przypadku przecięcie tej płaszczyzny z każdą ścianą wielościanu będzie pewnym odcinkiem.

Jeśli płaszczyzny przecinają się w linii prostej, wówczas nazywa się linię prostąpodążając za jedną z tych płaszczyzn na drugą.

Ogólnie rzecz biorąc, płaszczyzna przecięcia wielościanu przecina płaszczyznę każdej z jego ścian (a także każdą inną płaszczyznę przecięcia tego wielościanu). Przecina także każdą z linii, na których leżą krawędzie wielościanu.

Nazywa się linię prostą, wzdłuż której płaszczyzna cięcia przecina płaszczyznę dowolnej ściany wielościanupodążając za płaszczyzną cięcia na płaszczyźnie tej ściany, a punkt, w którym płaszczyzna przecięcia przecina linię zawierającą dowolną krawędź wielościanu, nazywa siępodążając za płaszczyzną cięcia NAtę linię prostą. Punkt ten jest jednocześnie śladem linii na płaszczyźnie cięcia. Jeżeli płaszczyzna cięcia przecina bezpośrednio ścianę wielościanu, to możemy mówić o śladzie płaszczyzny cięcia na ścianie i podobnie oślad płaszczyzny cięcia na krawędzi wielościanu, to znaczy o śladzie krawędzi na płaszczyźnie cięcia.

Ponieważ prostą wyznaczają jednoznacznie dwa punkty, aby znaleźć ślad płaszczyzny przecięcia na dowolnej innej płaszczyźnie, a w szczególności na płaszczyźnie dowolnej ściany wielościanu, wystarczy skonstruować dwa punkty wspólne płaszczyzn

Aby skonstruować ślad płaszczyzny przecięcia, a także skonstruować odcinek wielościanu za pomocą tej płaszczyzny, należy określić nie tylko wielościan, ale także płaszczyznę przecięcia. A konstrukcja płaszczyzny przekroju zależy od specyfikacji tej płaszczyzny. Główne sposoby definiowania płaszczyzny, a w szczególności płaszczyzny cięcia, są następujące:

trzy punkty nie leżące na tej samej linii;

linia prosta i punkt na niej nie leżący;

dwie równoległe linie;

dwie przecinające się linie;

punkt i dwie przecinające się linie;

Możliwe są także inne sposoby określenia płaszczyzny cięcia.

Dlatego wszystkie metody konstruowania przekrojów wielościanów można podzielić na metody.

Metody konstruowania przekrojów wielościanów

W zagadnieniach konstrukcyjnych stosowana jest metoda przekrojów wielościanów w stereometrii. Polega na umiejętności skonstruowania przekroju wielościanu i określenia rodzaju przekroju.

Istnieją trzy główne metody konstruowania przekrojów wielościanów:

Metoda aksjomatyczna:

Metoda śledzenia.

Metoda łączona.

Metoda współrzędnych.

Notatka że metoda śledzenia i metoda przekroju pomocniczego są odmianamiAksjomatyczna metoda konstruowania przekrojów.

Wyróżniamy także następujące metody konstruowania przekrojów wielościanów:

skonstruowanie przekroju wielościanu z płaszczyzną przechodzącą przez dany punkt równoległą do danej płaszczyzny;

skonstruowanie odcinka przechodzącego przez daną linię, równoległego do innej danej linii;

skonstruowanie odcinka przechodzącego przez dany punkt, równoległego do dwóch danych przecinających się linii;

skonstruowanie przekroju wielościanu z płaszczyzną przechodzącą przez daną linię prostopadłą do danej płaszczyzny;

konstruowanie przekroju wielościanu z płaszczyzną przechodzącą przez dany punkt prostopadle do danej prostej.

Główne działania składające się na metody konstruowania przekrojów to znalezienie punktu przecięcia prostej z płaszczyzną, zbudowanie linii przecięcia dwóch płaszczyzn, zbudowanie linii prostej równoległej do płaszczyzny, prostopadłej do płaszczyzny. Aby skonstruować linię przecięcia dwóch płaszczyzn, zwykle znajduje się dwa jej punkty i rysuje się przez nie linię. Aby skonstruować punkt przecięcia prostej i płaszczyzny, znajdź prostą na płaszczyźnie, która przecina daną. Następnie żądany punkt uzyskuje się na przecięciu znalezionej linii z podaną.

Rozważmy osobno te, które wymieniliśmymetody konstruowania przekrojów wielościanów:

Metoda śledzenia.

Metoda śledzenia opiera się (działa) na aksjomatach stereometrii, istotą metody jest skonstruowanie pomocniczej linii prostej, będącej obrazem linii przecięcia płaszczyzny cięcia z płaszczyzną dowolnej ściany figury. Najwygodniej jest skonstruować obraz linii przecięcia płaszczyzny cięcia z płaszczyzną dolnej podstawy. Ta liniazwany głównym śladem płaszczyzny cięcia . Za pomocą śladu łatwo jest skonstruować obrazy punktów płaszczyzny cięcia znajdujących się na bocznych krawędziach lub ścianach figury. Konsekwentnie łącząc obrazy tych punktów, otrzymujemy obraz pożądanego przekroju.

Zauważ to że podczas konstruowania głównego śladu płaszczyzny cięcia stosuje się następujące stwierdzenie.

Jeżeli punkty należą do płaszczyzny przecięcia i nie leżą na tej samej prostej, a ich rzut (środkowy lub równoległy) na płaszczyznę wybraną jako główną, punkty są odpowiednio następnie punkty przecięcia odpowiednich linii, to znaczy punkty i leżą na tej samej linii (ryc. 1, a, b).

Ryc.1.a Ryc.1.b

Ta linia prosta jest głównym śladem płaszczyzny cięcia. Ponieważ punkty leżą na głównej trasie, do jej skonstruowania wystarczy znaleźć dwa punkty z tych trzech.

Metoda przekrojów pomocniczych.

Ta metoda konstruowania odcinków wielościanów jest dość uniwersalna. W przypadkach, gdy pożądany ślad (lub ślady) płaszczyzny cięcia znajduje się poza rysunkiem, metoda ta ma nawet pewne zalety. Jednocześnie należy mieć na uwadze, że konstrukcje wykonywane tą metodą często okazują się „zatłoczone”. Jednak w niektórych przypadkach metoda odcinków pomocniczych okazuje się najbardziej racjonalna.

Metoda łączona

Istotą kombinowanej metody konstruowania odcinków wielościanów jest zastosowanie twierdzeń o równoległości linii i płaszczyzn w przestrzeni w połączeniu z metodą aksjomatyczną.

Metoda współrzędnych konstruowania przekrojów.

Istotą metody współrzędnych jest obliczenie współrzędnych punktów przecięcia krawędzi lub wielościanu z płaszczyzną przecięcia, co jest określone równaniem płaszczyzny. Równanie płaszczyzny cięcia jest obliczane na podstawie warunków problemowych.

Notatka że ta metoda konstruowania przekroju wielościanu jest akceptowalna dla komputera, ponieważ wiąże się z dużą ilością obliczeń i dlatego zaleca się realizację tej metody za pomocą komputera.

Naszym głównym zadaniem będzie zbudowanie odcinka wielościanu z płaszczyzną, tj. w konstruowaniu przecięcia tych dwóch zbiorów.

Konstrukcja przekrojów wielościanów

Przede wszystkim zauważamy, że przekrój wielościanu wypukłego jest wypukłym wielokątem płaskim, którego wierzchołki w ogólnym przypadku są punktami przecięcia płaszczyzny cięcia z krawędziami wielościanu, a boki z jego twarze.

Przykłady konstrukcji sekcji:

Metody definiowania przekroju są bardzo zróżnicowane. Najbardziej powszechną z nich jest metoda definiowania płaszczyzny przekroju przez trzy punkty, które nie leżą na tej samej prostej.

Przykład 1. Dla równoległościanu ABCDA 1 B 1 C 1 D 1 . Skonstruuj odcinek przechodzący przez punkty M, N, L.

Rozwiązanie:

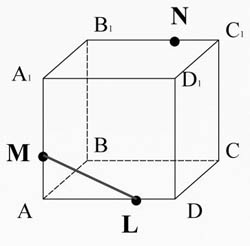
Połącz punkty M i L leżące w płaszczyźnie AA 1 D 1 D.

Przetnijmy prostą ML (należącą do przekroju) z krawędzią A 1 D 1 1 D 1 D. Zdobądź punkt X 1 .

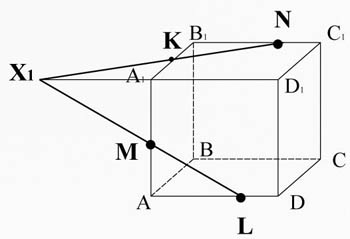
Punkt X1 leży na krawędzi A 1 D 1 , a stąd płaszczyzna A 1 B 1 C 1 D 1 , łączymy go oczkiem N leżącym w tej samej płaszczyźnie.

X 1 N przecina krawędź A 1 B 1 w punkcie K.

Połącz punkty K i M leżące w tej samej płaszczyźnie AA 1 B 1 B.

Znajdźmy linię prostą przecięcia płaszczyzny przekroju z płaszczyzną DD 1 C 1 C:

Przetnijmy prostą ML (należącą do przekroju) z krawędzią DD 1 , leżą w tej samej płaszczyźnie AA 1 D 1 D, dostajemy punkt X 2 .

Przetnijmy prostą KN (należącą do przekroju) z krawędzią D 1 C 1 , leżą w tej samej płaszczyźnie A 1 B 1 C 1 D 1 , otrzymujemy punkt X3;

Punkty X2 i X3 leżą na płaszczyźnie DD 1 C 1 C. Narysuj linię prostą X 2 X 3 , który przecina krawędź C 1 C w punkcie T i krawędź DC w punkcie P. Połącz punkty L i P leżące na płaszczyźnie ABCD.

Zatem problem uważa się za rozwiązany, jeśli zostaną znalezione wszystkie odcinki, wzdłuż których płaszczyzna przecina ściany wielościanu, co też zrobiliśmy. MKNTPL - wymagana sekcja.

Notatka. Ten sam problem konstruowania przekroju można rozwiązać, korzystając z właściwości płaszczyzn równoległych.

Z powyższego można stworzyć algorytm (regułę) rozwiązywania problemów tego typu.

Zasady konstruowania przekrojów wielościanów:

1. rysować linie proste przez punkty leżące w tej samej płaszczyźnie;

   Szukamy bezpośrednich przecięć płaszczyzny przekroju ze ścianami wielościanu, w tym celu:

Przykład 2. DL, M

Rozwiążmy metodą aksjomatyczną:

Narysujmy płaszczyznę pomocnicząDKM, który przecina krawędzie AB i BC w punktach E iF(postęp rozwiązania na ryc. 2.). Skonstruujmy „ślad” CM płaszczyzny przekroju na tej płaszczyźnie pomocniczej, znajdź punkt przecięcia CM i EF– punkt P. Punkt P, jakL, leży w płaszczyźnie ABC i można narysować linię prostą, wzdłuż której płaszczyzna przekroju przecina płaszczyznę ABC („ślad” przekroju w płaszczyźnie ABC).

Przykład 3. Na krawędziach AB i AD piramidy MABCD wyznaczamy odpowiednio punkty P i Q, środki tych krawędzi, a na krawędzi MC wyznaczamy punkt R. Skonstruujmy odcinek piramidy z płaszczyzną przechodzącą przez punkty P, Q i R.

Rozwiązanie przeprowadzimy metodą kombinowaną:

1). Jest oczywiste, że głównym śladem płaszczyzny PQR jest linia prosta PQ.

2). Znajdźmy punkt K, w którym płaszczyzna MAC przecina prostą PQ. Punkty K i R należą zarówno do płaszczyzny PQR, jak i płaszczyzny MAC. Dlatego rysując linię prostą KR, otrzymujemy linię przecięcia tych płaszczyzn.

3). Znajdźmy punkt N=AC BD, narysujmy linię prostą MN i znajdźmy punkt F=KR MN.

4). Punkt F jest punktem wspólnym płaszczyzn PQR i MDB, czyli płaszczyzny te przecinają się na prostej przechodzącej przez punkt F. Jednocześnie, ponieważ PQ jest linią środkową trójkąta ABD, to PQ jest równoległe do BD, oznacza to, że linia PQ jest równoległa do płaszczyzny MDB. Następnie płaszczyzna PQR przechodząca przez prostą PQ przecina płaszczyznę MDB po prostej równoległej do prostej PQ, czyli równoległej do prostej BD. Zatem w płaszczyźnie MDB przechodzącej przez punkt F rysujemy prostą równoległą do prostej BD.

5). Dalsze konstrukcje są wyraźnie widoczne na rysunku. W rezultacie otrzymujemy wielokąt PQD„RB” - pożądany przekrój

Rozważmy przekroje pryzmatu dla uproszczenia, czyli wygody logicznego myślenia, rozważmy przekroje sześcianu (ryc. 3.a):

Ryż. 3.a

Przekroje pryzmatu o płaszczyznach równoległych do krawędzi bocznych są równoległobokami. W szczególności przekroje ukośne są równoległobokami (ryc. 4).

def. Przekrój ukośny Pryzmat przecina płaszczyzna przechodząca przez dwie boczne krawędzie, które nie należą do tej samej ściany.

Wielokąt powstały w wyniku przekątnej pryzmatu jest równoległobokiem. Pytanie o liczbę przekątnychN-pryzmat kątowy jest trudniejszy niż kwestia liczby przekątnych. Sekcji będzie tyle, ile jest przekątnych u podstawy. Wiemy, że pryzmat wypukły ma u podstaw wypukłe wielokąty, a pryzmat wypukłyN-gon przekątnych. Można więc powiedzieć, że przekątnych jest o połowę mniej niż przekątnych.

Notatka: Konstruując odcinki równoległościanu na rysunku, należy wziąć pod uwagę fakt, że jeśli płaszczyzna przecięcia przecina dwie przeciwległe ściany na niektórych odcinkach, to odcinki te są równoległe „z właściwości równoległościanu, tj. Przeciwległe ściany równoległościanu są równoległe i równe.

Udzielimy odpowiedzi na najczęściej zadawane pytania:

Jakie wielokąty powstają po przecięciu sześcianu płaszczyzną?

„trójkąt, czworokąt, pięciokąt, sześciokąt”.

Czy sześcian można pociąć płaszczyzną na siedmiokąt? A co z ośmiokątem?

„nie mogą”.

3) Powstaje pytanie: jaka jest największa liczba boków wielokąta uzyskana przez przecięcie wielościanu płaszczyzną?

Największa liczba boków wielokąta uzyskana przez przecięcie wielościanu przez płaszczyznę jest równa liczbie ścian wielościanu .

Przykład 3. Skonstruuj przekrój pryzmatu A 1 B 1 C 1 D 1 ABCD płaszczyzną przechodzącą przez trzy punkty M, N, K.

Rozważmy przypadek położenia punktów M, N, K na powierzchni pryzmatu (rys. 5).

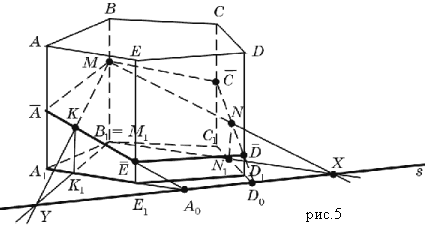
Rozważmy przypadek: W tym przypadku jest oczywiste, że M1 = B1.

Budowa:

Przykład 4. Skonstruuj odcinek równoległościanu ABCDA 1 B 1 C 1 D 1 płaszczyzna przechodząca przez punkty M, N, P (punkty zaznaczono na rysunku (rys. 6)).

Rozwiązanie:

Ryż. 6

Punkty N i P leżą w płaszczyźnie przekroju oraz w płaszczyźnie dolnej podstawy równoległościanu. Skonstruujmy linię prostą przechodzącą przez te punkty. Ta linia prosta jest śladem płaszczyzny cięcia na płaszczyźnie podstawy równoległościanu.

Kontynuujmy linię prostą, po której leży bok AB równoległościanu. Proste AB i NP przecinają się w pewnym punkcie S. Punkt ten należy do płaszczyzny przekroju.

Ponieważ punkt M również należy do płaszczyzny przekroju i przecina linię AA 1 w pewnym momencie X.

Punkty X i N leżą w tej samej płaszczyźnie ściany AA 1 D 1 D, połącz je i uzyskaj prostą XN.

Ponieważ płaszczyzny ścian równoległościanu są równoległe, to przez punkt M możemy narysować linię prostą do ściany A 1 B 1 C 1 D 1 , równolegle do prostej NP. Linia ta przetnie bok B 1 Z 1 w punkcie Y.

Podobnie rysujemy linię prostą YZ, równoległą do prostej XN. Łączymy Z z P i otrzymujemy żądaną sekcję - MYZPNX.

Przekroje piramidy płaszczyznami przechodzącymi przez jej wierzchołek są trójkątami. W szczególności trójkąty są przekrojami ukośnymi. Są to przekroje płaszczyzn przechodzących przez dwie niesąsiadujące ze sobą boczne krawędzie piramidy.

Przykład 4. Skonstruuj przekrój piramidy ABCDpłaszczyzna przechodząca przez punkty K,L, M.

Rozwiązanie:

1. Narysujmy kolejną płaszczyznę pomocnicząDCKi skonstruuj punkt przecięcia BLIDK – punkt E. Punkt ten należy do obu płaszczyzn pomocniczych (rys. 7, b);

   Znajdźmy punkt przecięcia odcinkówL.M.i EC (odcinki te leżą na płaszczyźnieBLC, ryc. 7, c) – pktF. KropkaFleży w płaszczyźnie przekroju i w płaszczyźnieDCK;

   Zróbmy bezpośredniKFi znajdź punkt przecięcia tej linii zDC- punktN(kropkaNnależy do sekcji). CzworobokKLNM– wymagana sekcja.

Rozwiążmy ten sam przykład inaczej .

Załóżmy, że w punktach KLi M skonstruowana sekcjaKLNM(ryc. 7). Oznaczmy przezFpunkt przecięcia przekątnych czworokątaKLNM. Zróbmy bezpośredniDFi oznacz przezF 1 jego punkt przecięcia z krawędzią ABC. KropkaF 1 pokrywa się z punktem przecięcia prostych AM i SC (F 1 jednocześnie należy do płaszczyzn AMDIDSK). KropkaF 1 łatwy w budowie. Następnie budujemy punktFjako punkt przecięciaDF 1 IL.M.. Następnie znajdujemy punktN.

Rozważana technika nazywa sięmetoda projektowania wewnętrznego . (W naszym przypadku mówimy o projekcie centralnym. CzworokątKMSA to rzut czworobokuKMNLz punktuD. W tym przypadku punkt przecięcia przekątnychKMNL- punktF– idzie do punktu przecięcia przekątnych czworobokuKMSA – punktF 1 .

Pole przekroju wielościanu.

Problem obliczenia pola przekroju wielościanu zwykle rozwiązuje się w kilku etapach. Jeżeli w zadaniu jest napisane, że zbudowano przekrój (lub narysowano płaszczyznę przekroju itp.), to w pierwszym etapie rozwiązania określany jest rodzaj figury uzyskanej w przekroju.

Należy to zrobić, aby wybrać odpowiedni wzór do obliczenia pola przekroju poprzecznego. Po wyjaśnieniu rodzaju figury uzyskanej w sekcji i wybraniu wzoru do obliczenia pola tej figury, przechodzimy bezpośrednio do pracy obliczeniowej.

W niektórych przypadkach może być łatwiej, jeśli nie ustalając rodzaju figury uzyskanej w sekcji, przejdziesz od razu do obliczenia jej pola za pomocą wzoru wynikającego z twierdzenia.

Twierdzenie o obszarze rzutu ortogonalnego wielokąta: Pole rzutu ortogonalnego wielokąta na płaszczyznę jest równe iloczynowi jego powierzchni i cosinusa kąta między płaszczyzną wielokąta a płaszczyzną projekcji: .

Prawidłowy wzór na obliczenie pola przekroju to: gdzie jest pole rzutu ortogonalnego figury uzyskanej w przekroju i jest to kąt między płaszczyzną cięcia a płaszczyzną, na którą rzutowana jest figura. Dzięki temu rozwiązaniu konieczne jest skonstruowanie rzutu ortogonalnego figury uzyskanej w przekroju i obliczenie

Jeśli w opisie problemu jest napisane, że należy zbudować przekrój i znaleźć pole powstałego przekroju, to w pierwszym etapie należy uzasadnić skonstruowanie danego przekroju, a następnie oczywiście określić rodzaj uzyskanej figury sekcja itp.

Zwróćmy uwagę na następujący fakt: skoro konstruuje się przekroje wielościanów wypukłych, to wielokąt przekroju również będzie wypukły, więc jego pole można obliczyć dzieląc go na trójkąty, czyli pole przekroju jest równe sumie pól trójkąty, z których jest zbudowany.

Zadanie 1.

– regularna trójkątna piramida o boku podstawy równym i wysokości równej Skonstruuj przekrój piramidy z płaszczyzną przechodzącą przez punkty, w których jest środek boku i oblicz jej pole (ryc. 8).

Rozwiązanie.

Przekrój piramidy to trójkąt. Znajdźmy jego pole.

Ponieważ podstawą piramidy jest trójkąt równoboczny, a punkt jest środkiem boku, jest to wysokość, a następnie .

Pole trójkąta można znaleźć:

Zadanie 2.

Boczna krawędź prostopadłościanu foremnego jest równa bokowi podstawy. Konstruuj przekroje pryzmatu z płaszczyznami przechodzącymi przez punktA, prostopadle do linii prostej Jeśli znajdziemy pole powstałego przekroju pryzmatu.

Rozwiązanie.

Skonstruujmy zadaną sekcję. Zróbmy to na podstawie rozważań czysto geometrycznych, na przykład w następujący sposób.

W płaszczyźnie przechodzącej przez daną prostą i dany punkt narysuj linię prostopadłą do prostej przechodzącej przez ten punkt (rys. 9). W tym celu wykorzystajmy fakt, że w trójkącie oznacza to, że jego mediana jest również wysokością tego trójkąta. Więc to jest proste.

Przez ten punkt rysujemy kolejną linię prostopadłą do tej linii. Narysujmy to na przykład w płaszczyźnie przechodzącej przez linię prostą. Jest oczywiste, że ta linia jest linią prostą

W ten sposób konstruowane są dwie przecinające się linie, prostopadłe do linii. Linie te definiują płaszczyznę przechodzącą przez punkt prostopadły do ​​tej linii, czyli wyznaczana jest płaszczyzna cięcia.

Skonstruujmy odcinek pryzmatu z tą płaszczyzną. Zauważ, że ponieważ linia jest równoległa do płaszczyzny. Następnie płaszczyzna przechodząca przez linię przecina płaszczyznę wzdłuż linii równoległej do linii, czyli linii. Narysujmy linię prostą przez punkt i połączmy powstały punkt z kropką.

Dany przekrój czworoboczny. Określmy jego powierzchnię.

Oczywiste jest, że czworokąt jest prostokątem, to znaczy jego pole wynosi

ryż. 9

Czy wiesz, jak nazywa się przekrój wielościanu przez płaszczyznę? Jeśli nadal wątpisz w poprawność swojej odpowiedzi na to pytanie, możesz to sprawdzić w prosty sposób. Sugerujemy wykonanie krótkiego testu poniżej.

Pytanie. Jaki numer ma figura przedstawiająca przekrój równoległościanu przez płaszczyznę?

Zatem prawidłowa odpowiedź znajduje się na rysunku 3.

Jeśli odpowiesz poprawnie, jest to potwierdzenie, że rozumiesz, z czym masz do czynienia. Ale niestety nawet poprawna odpowiedź na pytanie testowe nie gwarantuje najwyższych ocen na lekcjach na temat „Przekroje wielościanów”. Przecież najtrudniejszą rzeczą nie jest rozpoznawanie przekrojów na gotowych rysunkach, choć to też jest bardzo ważne, ale ich konstrukcja.

Na początek sformułujmy definicję przekroju wielościanu. Zatem przekrój wielościanu jest wielokątem, którego wierzchołki leżą na krawędziach wielościanu, a boki leżą na jego ścianach.

Poćwiczmy teraz szybkie i dokładne konstruowanie punktów przecięcia daną linię prostą z daną płaszczyzną. Aby to zrobić, rozwiążmy następujący problem.

Skonstruuj punkty przecięcia prostej MN z płaszczyznami dolnej i górnej podstawy graniastosłupa trójkątnego ABCA 1 B 1 C 1, pod warunkiem, że punkt M należy do krawędzi bocznej CC 1, a punkt N do krawędzi BB 1.

Zacznijmy od przedłużenia prostej MN w obu kierunkach na rysunku (rys. 1). Następnie, aby uzyskać wymagane w zadaniu punkty przecięcia, przedłużamy linie leżące w podstawach górnej i dolnej. I teraz nadchodzi najtrudniejszy moment w rozwiązaniu problemu: które linie w obu bazach należy przedłużyć, skoro każda z nich ma trzy linie.

Aby poprawnie zakończyć ostatni etap budowy, konieczne jest określenie, które z bezpośrednich podstaw znajdują się w tej samej płaszczyźnie, co interesująca nas prosta MN. W naszym przypadku jest to proste CB w dolnej części i C 1 B 1 w górnej podstawie. I to właśnie je rozciągamy, aż przetną się z prostą NM (ryc. 2).

Powstałe punkty P i P 1 są punktami przecięcia prostej MN z płaszczyznami górnej i dolnej podstawy trójkątnego pryzmatu ABCA 1 B 1 C 1 .

Po przeanalizowaniu przedstawionego problemu można przejść bezpośrednio do konstruowania przekrojów wielościanów. Kluczowym punktem będzie tutaj rozumowanie, które pomoże Ci osiągnąć pożądany rezultat. W rezultacie docelowo spróbujemy stworzyć szablon, który będzie odzwierciedlał kolejność działań przy rozwiązywaniu problemów tego typu.

Rozważmy zatem następujący problem. Skonstruuj odcinek trójkątnego pryzmatu ABCA 1 B 1 C 1 z płaszczyzną przechodzącą przez punkty X, Y, Z należące odpowiednio do krawędzi AA 1, AC i BB 1.

Rozwiązanie: Narysujmy rysunek i określmy, które pary punktów leżą na tej samej płaszczyźnie.

Pary punktów X i Y, X i Z można połączyć, ponieważ leżą w tej samej płaszczyźnie.

Skonstruujmy dodatkowy punkt, który będzie leżał na tej samej ścianie co punkt Z. W tym celu przedłużymy linie XY i CC 1, ponieważ leżą w płaszczyźnie ściany AA 1 C 1 C. Wynikowy punkt nazwijmy P.

Punkty P i Z leżą w tej samej płaszczyźnie - w płaszczyźnie ściany CC 1 B 1 B. Dlatego możemy je połączyć. Prosta PZ przecina krawędź CB w pewnym punkcie, nazwijmy ją T. Punkty Y i T leżą w dolnej płaszczyźnie pryzmatu, połącz je. W ten sposób powstał czworobok YXZT i jest to pożądany przekrój.

Podsumujmy. Aby skonstruować odcinek wielościanu z płaszczyzną, należy:

1) poprowadzić linie proste przez pary punktów leżących na tej samej płaszczyźnie.

2) znajdź linie, wzdłuż których przecinają się płaszczyzny przekroju i ściany wielościanu. Aby to zrobić, należy znaleźć punkty przecięcia prostej należącej do płaszczyzny przekroju z linią prostą leżącą w jednej ze ścian.

Proces konstruowania przekrojów wielościanów jest skomplikowany, ponieważ w każdym konkretnym przypadku jest inny. I żadna teoria nie opisuje tego od początku do końca. Tak naprawdę istnieje tylko jeden pewny sposób, aby nauczyć się szybko i dokładnie konstruować przekroje dowolnego wielościanu - jest to ciągła praktyka. Im więcej sekcji zbudujesz, tym łatwiej będzie Ci to zrobić w przyszłości.

blog.site, przy kopiowaniu materiału w całości lub w części wymagany jest link do oryginalnego źródła.