Wzór Picka

1. Wprowadzenie

2. Wzór Peaka. Wystawa I.

Dowód II.

Dowód Sz.

3. Cele.

4. Wzór na pole wielokąta za pomocą współrzędnych wierzchołków.

5. Zadania.

6. Literatura

Wzór Peaka.

1. Wprowadzenie.

Czerpiemy mądrość z historii,

w poezji - dowcip,

w matematyce - wgląd.

F. Bekon

Fabuła rozwinie się na zwykłej kartce papieru w kratkę.

Linie biegnące wzdłuż boków komórek tworzą siatkę, a wierzchołki komórek stanowią węzły tej siatki. Narysujmy na arkuszu wielokąt z wierzchołkami w węzłach i znajdźmy jego pole.

Można go szukać na różne sposoby. Na przykład możesz pociąć wielokąt na dość proste kształty, znaleźć ich pola i dodać je.

Ale czeka nas tutaj wiele kłopotów. Figurę można łatwo podzielić na prostokąty, trapezy i trójkąty, a jej pole oblicza się bez wysiłku.

Chociaż wielokąt wygląda dość prosto, obliczenie jego pola wymaga dużo pracy. A co by było, gdyby wielokąt wyglądał bardziej fantazyjnie? Okazuje się, że pola wielokątów, których wierzchołki znajdują się w węzłach siatki, można obliczyć znacznie prościej: istnieje wzór, który wiąże ich pole z liczbą węzłów leżących wewnątrz i na granicy wielokąta. Ta wspaniała i prosta formuła nazywa się formułą Pick.

2. Wzór Peaka.

Wierzchołki wielokąta (niekoniecznie wypukłego) znajdują się w węzłach sieci liczb całkowitych. Wewnątrz znajdują się węzły sieci B, a na granicy węzły G. Udowodnijmy, że jego pole jest równe B + – 1 (Wybierz formułę).

Wystawa I.

Rozważmy wielokąt, którego wierzchołki znajdują się w węzłach sieci całkowitej, to znaczy mają współrzędne całkowite.

Dzielimy wielokąt na trójkąty z wierzchołkami w węzłach sieci, niezawierające żadnych węzłów ani wewnątrz, ani po bokach.

Oznaczmy:

N– liczba boków wielokąta,

M– liczba trójkątów o wierzchołkach w węzłach sieci, które nie zawierają węzłów ani wewnątrz, ani po bokach,

B – liczba węzłów wewnątrz wielokąta,

Г – liczba węzłów po bokach, łącznie z wierzchołkami.

Pole wszystkich tych trójkątów jest takie samo i równe.

Dlatego obszar wielokąta wynosi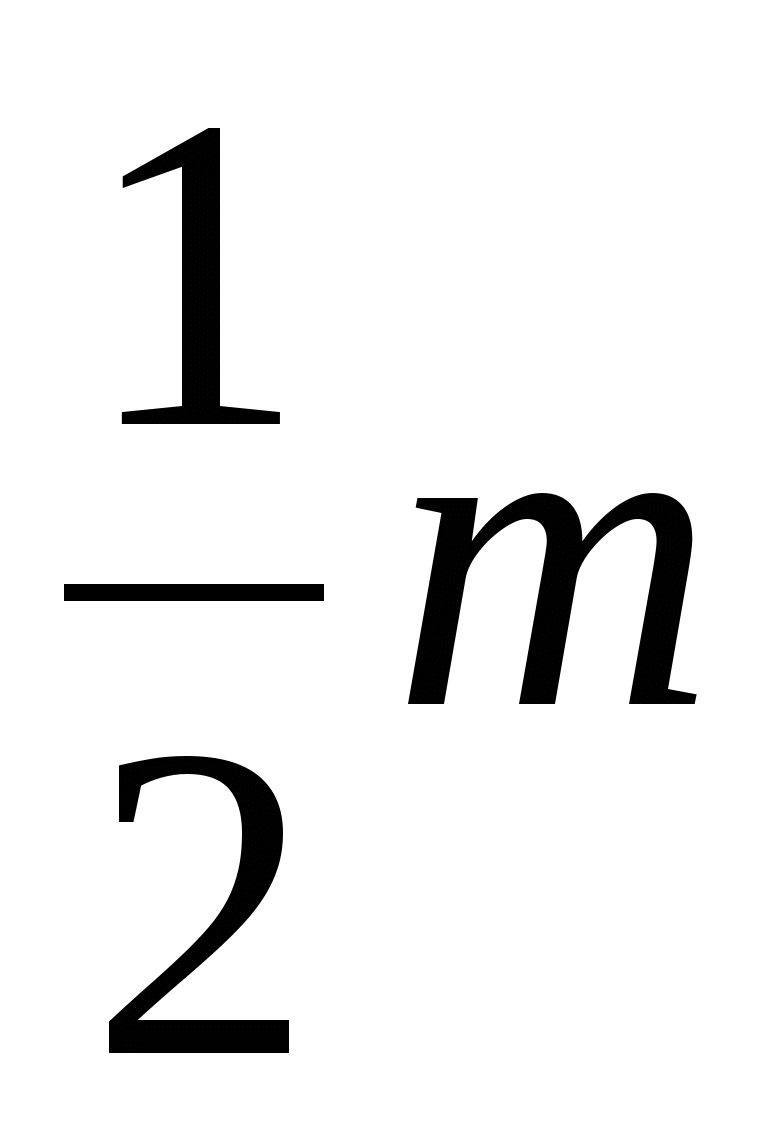
.

180 0 M .

Teraz znajdźmy tę kwotę w inny sposób.

Suma kątów z wierzchołkiem w dowolnym węźle wewnętrznym wynosi 360 0.

Wtedy suma kątów z wierzchołkami we wszystkich węzłach wewnętrznych jest równa 360 0 V.

Całkowita suma kątów dla węzłów po bokach, ale nie na wierzchołkach, wynosi 180 0 (G - N).

Suma kątów w wierzchołkach wielokąta wynosi 180 0 ( N – 2) .

Całkowita suma kątów wszystkich trójkątów wynosi 360 0 V + 180 0 (G – N) + 180 0 (N – 2).

Więc 180 0 M= 360 0 V + 180 0 (G – N) + 180 0 (N – 2),

180 0 M= 360 0 V + 180 0 G – 180 0 N + 180 0 N– 180 0 2,

180 0 M= 360 0 V + 180 0 G – 360 0,

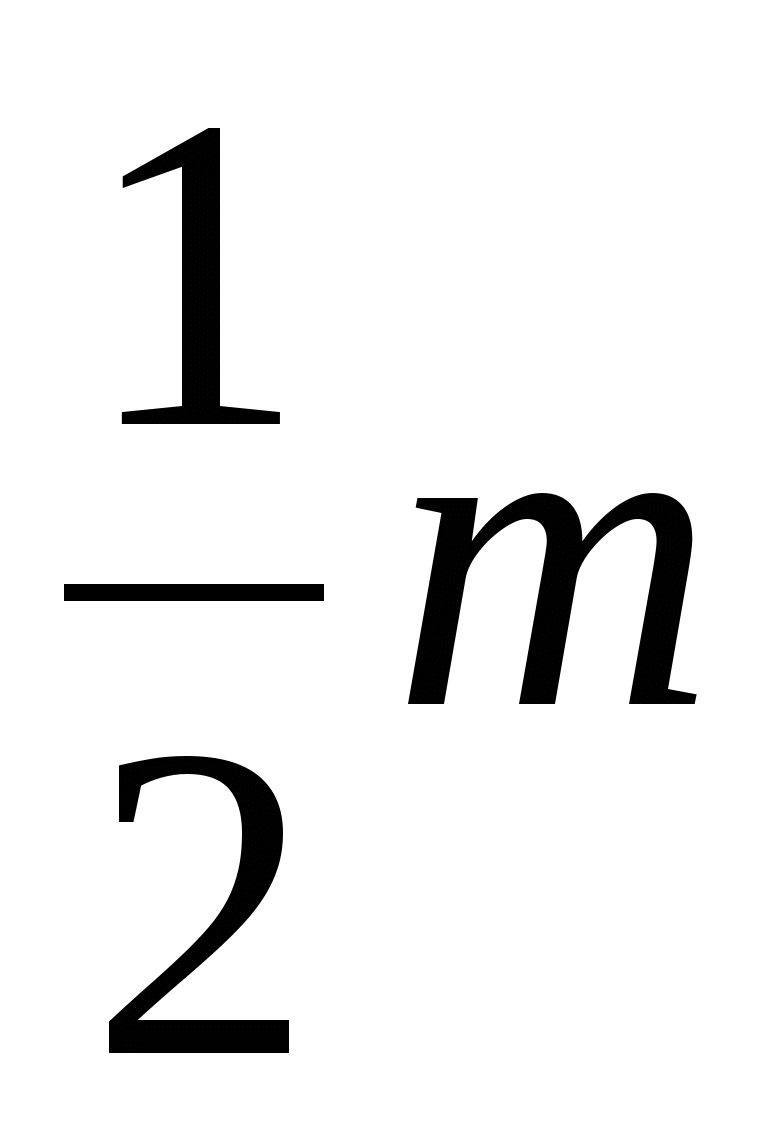= B + – 1 ,

z czego otrzymujemy wyrażenie na pole S wielokąta:

S= B + – 1 ,

znany jako wzór Picka.

Na rysunku: B = 24, D = 9, zatemS = 24 + – 1 = 27,5.

Znajdźmy obszar pierwszego wielokąta, korzystając ze wzoru Peaka:

B = 28 (zielone kropki);

G = 20 (niebieskie kropki).

Otrzymujemy, S =
= 37 jednostek kwadratowych

Dowód II.

Każdemu wielokątowi M, którego wierzchołki znajdują się w węzłach sieci całkowitej, przypisujemy liczbę f (M) =
, gdzie sumowanie odbywa się po wszystkich węzłach sieci należących do M, oraz kąt definiuje się następująco: =
dla wewnętrznego punktu wielokąta, =
dla punktu granicznego innego niż wierzchołek, oraz – kąt wierzchołkowy, jeżeli węzeł ten jest wierzchołkiem. Łatwo zobaczyć, że f(M) =
+
= B + – 1. Pozostaje sprawdzić, czy liczba f (M) jest równa polu wielokąta M.

Niech wielokąt M zostanie pocięty na wielokąty M 1 i M 2 z wierzchołkami w węzłach sieci. Następnie f (M) = f (M 1) + f (M 2), ponieważ dla każdego węzła dodawane są kąty. Zatem, jeśli wzór Picka jest prawdziwy dla dwóch wielokątów M, M 1 i M 2, to jest on również prawdziwy dla trzeciego.

Jeśli M jest prostokątem o bokach P I Q, następnie skierowane wzdłuż linii siatki

fa (M) = (p – 1)(q – 1) +
= p.p.

W tym przypadku obowiązuje wzór Peaka. Dzieląc prostokąt M o przekątnej na trójkąty M 1 i M 2 i wykorzystując fakt, że f (M) = f (M 1) + f (M 2) i f (M 1) = f (M 2), to łatwo jest udowodnić słuszność wzoru Picka dla dowolnego trójkąta prostokątnego o ramionach skierowanych wzdłuż linii siatki. Wycinając kilka takich trójkątów z prostokąta, możesz uzyskać dowolny trójkąt.

Aby zakończyć dowód wzoru Picka, pozostaje zauważyć, że dowolny wielokąt można pociąć na trójkąty za pomocą rozłącznych przekątnych.

Dowód Sz.

Zależność pola figury od liczby węzłów wchodzących w skład tej figury jest szczególnie wyraźnie widoczna w przypadku prostokąta.

Pozwalać ABCD- prostokąt z wierzchołkami w węzłach i bokami biegnącymi wzdłuż linii siatki.

Oznaczmy przez W liczba węzłów leżących wewnątrz prostokąta i przez G- liczba węzłów na jego granicy. Przesuńmy siatkę o połowę komórki w prawo i połowę komórki w dół.

Następnie obszar prostokąta można „rozdzielić” pomiędzy węzłami w następujący sposób: każdy z W węzły „kontrolują” całą komórkę przesuniętej siatki, każda z nich G– 4 węzły graniczne niebędące narożnikami to połowa komórki, a każdy z punktów narożnych to ćwierć komórki. Dlatego obszar prostokąta S jest równy

Zatem dla prostokątów z wierzchołkami w węzłach i bokami wzdłuż linii siatki ustaliliśmy wzór

Udowodnimy, że wzór ten jest prawdziwy nie tylko dla prostokątów, ale także dla dowolnych wielokątów z wierzchołkami w węzłach siatki.

Oznaczmy przez S M obszar wielokątaM z wierzchołkami w węzłach i przezP M – rozmiar
, GdzieW M – liczba węzłów wewnątrzM, A G M - liczba węzłów na granicy. Następnie wzór Peaka można zapisać jako
.

Dowód wzoru podzielimy na kilka etapów.

Krok 1.

Jeśli wielokątM z wierzchołkami w węzłach siatki pociętymi na 2 wielokątyM 1 I M 2 , wówczas również mający wierzchołki tylko w węzłach siatki
. Niech wielokątM pociąć na wielokątyM 1 I M 2 z wierzchołkami w węzłach segmentu AB. Wszystkie węzły z wyjątkiem tych, które należą do segmentuAB, wnieś równy udział w lewą i prawą stronę wzoru. Rozważmy węzły leżące na odcinku AB.

Jeśli taki węzeł leży pomiędzy A i B (na przykład C), to dla wielokątaM jest wewnętrzny i dla wielokątówM 1 I M 2 – graniczny. Dlatego jego wkład wP M jest równe 1 i w każdym z wyrażeń
I
– 0,5 każdy, czyli wkład takiego węzła doP M I
są równe.

Rozważmy węzły A i B. Są to węzły graniczne dla obu M, i dla M 1 , M 2 .

Dlatego wkład każdego z tych węzłów wP M równy 0,5 cala
- jednostka. Oznacza to, że całkowity udział węzłów A i B wP M jest równe 1, czyli o 1 mniej niż ich udział w
. Ale
, A .

Z całkowitego „wkładu” wszystkich węzłów P M 1 jest odejmowane i od
2 jest odejmowane, co kompensuje różnicę we wkładach węzłów A i B.

Więc,
.

Krok 2.

Jeśli wielokąt M z wierzchołkami w węzłach siatki pociętymi na dwa wielokąty M 1 I M 2 (również z wierzchołkami w węzłach), a wzór jest poprawny dla niektórych dwóch wielokątów MM 1 , M 2 , to dotyczy to również trzeciego wielokąta.

Niech tak będzie npM 1 I M 2 , to jest
. Następnie (w pierwszym kroku), ale (wg pierwszy krok) ostatnie wyrażenie jest równeP M , i równość
i istnieje wzór na Szczyt.

Krok 3.

Udowodnimy wzór Peaka na trójkąt prostokątny z wierzchołkami w węzłach siatki i ramionami leżącymi na liniach siatki.

Trójkąt ABC zbuduj go w kształcie prostokąta ABCD .

W przypadku prostokątów wzór Picka jest poprawny: S ABCD = P ABCD . Według pierwszego kroku P ABCD = P ABC + P ACD , P ABC = P ACD , Więc P ABCD = 2P ABC . Ale S ABCD = 2 S ABC . Dlatego S ABC = P ABC .

Krok 4.

Wzór Picka jest prawdziwy dla dowolnego trójkąta z wierzchołkami w węzłach siatki.

Po zbadaniu rysunku łatwo jest to zrozumieć: każdy taki trójkąt można uzyskać, „odcinając” z pewnego prostokąta o bokach wzdłuż linii siatki, kilka prostokątów i trójkątów prostokątnych z nogami na liniach siatki. A ponieważ wzór Picka jest prawdziwy dla prostokątów i trójkątów prostokątnych, to (pamiętaj o kroku 2) jest on również prawdziwy dla pierwotnego trójkąta.

Udowodniliśmy, że jeśli wielokąt można pociąć na trójkąty o wierzchołkach w węzłach siatki, to wzór Peaka jest dla niego prawdziwy.

3. Cele.

Znajdź obszar figur:

1
.

B=9

G = 4

B=9

G = 5

Wielokąt bez samoprzecięć nazywa się kratą, jeśli wszystkie jego wierzchołki znajdują się w punktach o współrzędnych całkowitych (w kartezjańskim układzie współrzędnych).

Twierdzenie Picka

Formuła

Dajmy sobie jakiś wielokąt kratowy o niezerowym polu powierzchni.

Oznaczmy jego pole przez ; liczba punktów o współrzędnych całkowitych leżących ściśle wewnątrz wielokąta przelotowego; liczba punktów o współrzędnych całkowitych leżących na bokach wielokąta przelotowego.

Następnie relacja wywołana Wzór Picka:

W szczególności, jeśli dla pewnego wielokąta znane są wartości I i B, wówczas jego powierzchnię można obliczyć jako , nawet nie znając współrzędnych jego wierzchołków.

Zależność tę odkrył i udowodnił austriacki matematyk Georg Alexander Pick w 1899 roku.

Dowód

Dowód przeprowadza się w kilku etapach: od najprostszych figur po dowolne wielokąty:

Uogólnienie na wyższe wymiary

Niestety, ta prosta i piękna formuła Peake'a nie daje się dobrze uogólnić na wyższe wymiary.

Wyraźnie wykazał to Reeve, który w 1957 roku zaproponował rozważenie czworościanu (obecnie zwanego czworościan Reeve’a) z następującymi wierzchołkami:

gdzie jest dowolną liczbą naturalną. Wtedy ten czworościan dla każdego nie zawiera ani jednego punktu o współrzędnych całkowitych w środku, a na jego granicy znajdują się tylko cztery punkty , , i żadnych innych. Zatem objętość i powierzchnia tego czworościanu może być różna, natomiast liczba punktów wewnątrz i na granicy pozostaje niezmieniona; dlatego wzór Picka nie pozwala na uogólnienia nawet na przypadek trójwymiarowy.

Niemniej jednak nadal istnieje pewne podobne uogólnienie na przestrzenie o wyższych wymiarach - to Wielomiany Ehrharta(Wielomian Ehrharta), ale są one bardzo złożone i zależą nie tylko od liczby punktów wewnątrz i na brzegu figury.

Aby oszacować powierzchnię wielokąta na papierze w kratkę, wystarczy policzyć, ile komórek obejmuje ten wielokąt (powierzchnię komórki przyjmujemy jako jeden). Dokładniej, jeśli S- pole wielokąta, - liczba komórek znajdujących się w całości wewnątrz wielokąta, oraz - liczba komórek, które mają przynajmniej jeden punkt wspólny z wnętrzem wielokąta.

Poniżej rozważymy tylko takie wielokąty, których wszystkie wierzchołki leżą w węzłach kraciastego papieru - w tych, w których przecinają się linie siatki. Okazuje się, że dla takich wielokątów można określić następujący wzór:

gdzie jest teren, R- liczba węzłów leżących ściśle wewnątrz wielokąta.

Formuła ta nazywa się „formułą Pick” – od nazwiska matematyka, który ją odkrył w 1899 roku.

Proste trójkąty

Pole dowolnego trójkąta narysowanego na papierze w kratkę można łatwo obliczyć, przedstawiając go jako sumę lub różnicę pól trójkątów prostokątnych i prostokątów, których boki podążają za liniami siatki przechodzącymi przez wierzchołki narysowanego trójkąta. Robiąc to na przykład dla trójkątów pokazanych na rysunku 1.34, możesz upewnić się, że pole jest zawsze równe liczbie „otrzymanej” - liczbie w postaci, gdzie jest liczbą całkowitą.

Nazwijmy trójkąt prostym, jeśli nie ma w nim ani po bokach, z wyjątkiem wierzchołków, żadnych węzłów siatki. Wszystkie proste trójkąty na ryc. 1,34 ma powierzchnię. Zobaczymy, że nie jest to przypadkowe.

Zadanie. Trzy koniki polne (trzy punkty) w początkowej chwili siadają na trzech wierzchołkach jednej komórki, a następnie zaczynają „bawić się w żabę”: każdy może przeskoczyć jeden z dwóch pozostałych, po czym kończy się w punkcie symetrycznym względem siebie do siebie (ryc. 1.35 wyraźnie widać, że po dowolnej liczbie takich skoków koniki polne wpadają w węzły kraciastego papieru). W jakich potrójnych punktach mogą znaleźć się koniki polne po kilku skokach?

Nazwijmy trójkąt osiągalnym, jeśli na jego wierzchołkach mogą jednocześnie pojawić się trzy koniki polne, które początkowo znajdowały się w trzech wierzchołkach jednej komórki; skokiem nazwiemy transformację trójkąta, która polega na tym, że jeden z wierzchołków przechodzi do punktu, który jest symetryczny względem któregokolwiek z dwóch pozostałych wierzchołków (te dwa wierzchołki pozostają na miejscu).

Twierdzenie 1. Następujące trzy właściwości trójkątów z wierzchołkami w węzłach papieru w kratkę są sobie równoważne:

1) trójkąt ma pole,

2) trójkąt jest prosty,

3) trójkąt jest osiągalny.

Zapoznajmy się z następującymi właściwościami prostego trójkąta, które prowadzą do ważności tego twierdzenia.

1. Pole trójkąta nie zmienia się podczas skoku.

2. Każdy osiągalny trójkąt ma pole.

3. Jeśli ukończysz prosty trójkąt ABC do równoległoboku ABCD, to nie będzie żadnych węzłów (nie licząc wierzchołków) ani wewnątrz, ani po bokach tego równoległoboku.

4. Z prostego trójkąta podczas skoku uzyskuje się prosty trójkąt.

5. Z prostego trójkąta jeden z kątów jest rozwarty lub prosty (przy czym ten drugi przypadek jest możliwy tylko w przypadku trójkąta, którego trzy wierzchołki należą do jednej komórki; taki prosty trójkąt o bokach 1, 1 nazwiemy minimalnym).

6. Z dowolnego prostego trójkąta, który nie jest minimalny, jednym skokiem można uzyskać trójkąt, którego najdłuższy bok jest mniejszy od najdłuższego boku pierwotnego.

7. Dowolny prosty trójkąt można przekształcić w trójkąt minimalny za pomocą skończonej liczby skoków.

8. Dowolny prosty trójkąt jest osiągalny.

9. Każdy prosty trójkąt ma pole.

10. Dowolny trójkąt można pociąć na proste.

11. Pole dowolnego trójkąta jest równe i za każdym razem, gdy jest dzielony na liczby pierwsze, ich liczba jest równa M.

12. Dowolny trójkąt o polu jest prosty.

13. Dla dowolnych dwóch węzłów A I W kraty, na odcinku, pomiędzy którym nie ma innych węzłów, znajduje się węzeł Z taki, że trójkąt ABC- prosty.

14. Węzeł Z w poprzedniej właściwości zawsze możesz wybrać taki kąt ŚREDNICA będzie tępy lub prosty.

15. Podzielmy płaszczyznę szachownicy na równe równoległoboki tak, aby wszystkie węzły były wierzchołkami równoległoboków. Wtedy każdy z trójkątów, w który przecina się jeden z tych równoległoboków przez jego przekątną, jest prosty.

16. (Rewers 15). Trójkąt ABC- proste wtedy i tylko wtedy, gdy uzyskano wszystkie możliwe trójkąty ABC tłumaczenia równoległe przenoszące węzeł A w różne węzły sieci, nie nakładają się na siebie.

17. Jeśli siatka - węzły kraciastego papieru - zostanie podzielona na cztery podsieci z komórkami (ryc. 1.36), wówczas wierzchołki prostego trójkąta z konieczności wpadną na trzy różne podsieci (wszystkie trzy mają różne oznaczenia).

Poniższe dwie właściwości dostarczają odpowiedzi na problem trzech koników polnych.

18. Trzy koniki polne mogą jednocześnie trafić w te i tylko te trójki punktów, które służą jako wierzchołki prostego trójkąta i mają ten sam znak, co odpowiadające im wierzchołki początkowego trójkąta.

19. Dwa koniki polne mogą jednocześnie trafić w te i tylko te pary węzłów odpowiednich znaków, na odcinku pomiędzy którymi nie ma innych węzłów.

Triangulacja wielokątów

Rozważymy konkretny typ wielokątów na papierze w kratkę, który odpowiada wartościom w formule Pick. Ale od tego konkretnego przypadku można przejść od razu do najbardziej ogólnego, korzystając z twierdzenia o pocięciu dowolnego wielokąta na trójkąty (papier w kratkę nie jest już potrzebny).

Niech na płaszczyźnie będzie dany wielokąt i jakiś zbiór skończony DO punkty leżące wewnątrz wielokąta i na jego granicy (a wszystkie wierzchołki wielokąta należą do zbioru DO).

Triangulacja z wierzchołkami DO nazywa się podziałem danego wielokąta na trójkąty o wierzchołkach w zbiorze DO tak, że każdy punkt z DO służy jako wierzchołek każdego z trójkątów triangulacyjnych, do których należy ten punkt (to znaczy punktów z DO nie wpadaj do środka ani na boki trójkątów, rys. 1,37).

Twierdzenie 2. a) Dowolne N-trójkąt można podzielić po przekątnej na trójkąty, a liczba trójkątów będzie równa N- 2 (ten podział jest triangulacją z wierzchołkami na wierzchołkach N-gon).

b) Niech zostanie zaznaczona granica wielokąta R punkty (w tym wszystkie wierzchołki), wewnątrz - więcej I zwrotnica. Następnie następuje triangulacja z wierzchołkami w zaznaczonych punktach i liczba trójkątów takiej triangulacji będzie równa.

Oczywiście a) jest szczególnym przypadkiem b), kiedy.

Ważność tego twierdzenia wynika z następujących stwierdzeń.

1) Od wierzchołka największego kąta N-gon(), zawsze możesz narysować przekątną, która leży całkowicie wewnątrz wielokąta.

2) Jeśli N-kwadrat jest cięty po przekątnej R-kwadrat i Q-Gon, zatem.

3) Suma kątów N-gon jest równy.

4) Dowolny N-trójkąt można podzielić po przekątnej na trójkąty.

5) Dla dowolnego trójkąta, wewnątrz i na granicy którego zaznaczono kilka punktów (w tym wszystkie trzy jego wierzchołki), zachodzi triangulacja z wierzchołkami w zaznaczonych punktach.

6) To samo dotyczy każdego N-gon.

7) Liczba trójkątów triangulacyjnych jest równa, gdzie I I R- liczba zaznaczonych kilku punktów odpowiednio wewnątrz i na granicy wielokąta. Nazwijmy partycję N-gon na kilka wielokątów jest poprawny, jeśli każdy wierzchołek jednego z wielokątów przegrody służy jako wierzchołek wszystkich pozostałych wielokątów przegrody, do której należy. 8) Jeśli z wierzchołków k-gony, na które są podzielone w odpowiedni sposób N-gon, I wierzchołki leżą wewnątrz i R- na granicy N-gon, a następnie ilość k- gony są równe

9) Jeżeli punkty płaszczyzny i odcinki zakończone w tych punktach tworzą wielokąt poprawnie podzielony na wielokąty, to (ryc. 1.38)

Z twierdzeń 1 i 2 wynika wzór na szczyt:

1.5 Twierdzenie Pitagorasa o sumie pól kwadratów zbudowanych na bokach trójkąta prostokątnego

Twierdzenie. Suma pól kwadratów zbudowanych na bokach trójkąta prostokątnego jest równa polu kwadratu zbudowanego na przeciwprostokątnej tego trójkąta. Pozwalać ABC(ryc. 1.39) jest trójkątem prostokątnym i BDEA, AFGE I BCKH- kwadraty zbudowane na nogach i przeciwprostokątnej; musisz udowodnić, że suma pól pierwszych dwóch kwadratów jest równa powierzchni trzeciego kwadratu.

Przeprowadźmy Słoneczny. Następnie kwadrat BCKH zostanie podzielony na dwa prostokąty. Udowodnimy, że prostokąt BLMH równy kwadratowi BDEA i prostokąt LCKM równy kwadratowi AFGC.

Narysujmy linie pomocnicze DC I JAKIŚ. Rozważ trójkąty DCB I ABH. Trójkąt DCB mając podstawę BD, wspólne z kwadratem BDEA i wysokość CN, równa wysokości AB ten kwadrat jest równy połowie kwadratu. Trójkąt AVN mając podstawę VN, wspólne z prostokątem BLMH i wysokość AR, równa wysokości B.L. tego prostokąta o wielkości równej jego połowie. Porównując te dwa trójkąty ze sobą, stwierdzamy, że tak BD = VA I BC = VN(jak boki kwadratu);

Ponadto, DCB = AVN, ponieważ każdy z tych kątów składa się ze wspólnej części - ABC i kąt prosty. Zatem trójkąty AVN I BCD są równe. Wynika z tego, że prostokąt BLMN równy kwadratowi BDEA. W ten sam sposób udowodniono, że prostokąt LGKM równy kwadratowi AFGC. Wynika z tego, że kwadrat VSKN równa sumie kwadratów BDEA I AFGC.

Obliczanie pola figury.

Wybierz metodę

Praca uczennicy klasy 5B Gimnazjum nr 23 MBOU w Irkucku

Balsukova Aleksandra

Kierownik: Khodyreva T.G.

2014

Obliczanie pola figury. Wybierz metodę

Przedmiot badań : problemy na papierze w kratkę

Przedmiot badań : problemy obliczania pola wielokąta na papierze w kratkę, metody i techniki ich rozwiązywania.

Metody badawcze : porównanie, uogólnienie, analogie, badanie literatury i zasobów Internetu, analiza informacji.

Cel badania:

wybierz główną, interesującą i zrozumiałą informację

Analizuj i usystematyzuj otrzymane informacje

Znajdź różne metody i techniki rozwiązywania problemów na papierze w kratkę

sprawdź wzory do obliczania pól figur geometrycznych za pomocą wzoru Pick

Stwórz elektroniczną prezentację pracy, prezentującą zebrany materiał

Geometria jest najpotężniejszym środkiem wyostrzającym nasze zdolności umysłowe i umożliwiającym nam prawidłowe myślenie i rozumowanie.

(G. Galileo)

Trafność tematu

Pasja do matematyki często zaczyna się od myślenia o problemie. Tak więc, studiując temat „Obszar wielokątów”, pojawia się pytanie, czy istnieją problemy inne niż problemy omówione w podręczniku. Do takich problemów zaliczają się problemy na papierze w kratkę. Jaka jest specyfika takich problemów, czy istnieją specjalne metody i techniki rozwiązywania problemów na papierze w kratkę. Na lekcji matematyki nauczyciel przedstawił nam ciekawą metodę obliczania wielokątów. Zacząłem studiować literaturę i zasoby internetowe na ten temat. Wydawać by się mogło, że coś fascynującego można znaleźć na płaszczyźnie w kratkę, czyli na niekończącej się kartce papieru, ułożonej w jednakowe kwadraty. Okazuje się, że zadania związane z papierem w kratkę są dość różnorodne. Nauczyłem się obliczać pole wielokątów narysowanych na kartce papieru w kratkę. W przypadku wielu problemów zapisanych na papierze w kratkę nie ma ogólnej reguły rozwiązywania ani konkretnych metod i technik. To właśnie ich właściwość decyduje o ich wartości dla rozwoju nie konkretnej zdolności czy umiejętności akademickiej, ale w ogóle umiejętności myślenia, refleksji, analizowania, szukania analogii, czyli zadania te rozwijają umiejętność myślenia w najszerszym znaczeniu.

Dowiedziałem się też, że takie zadania są uwzględniane w materiałach testowo-pomiarowych Państwowej Akademii Nauk i Jednolitego Egzaminu Państwowego. Dlatego uważam, że przestudiowanie tego materiału jest przydatne nie tylko do wykorzystania go w dalszym procesie edukacyjnym, ale także do rozwiązywania niestandardowych problemów olimpijskich.

2.Pojęcie obszaru

Kwadrat- numeryczna charakterystyka dwuwymiarowej figury geometrycznej, pokazująca wielkość tej figury. Historycznie rzecz biorąc, nazywano to obliczaniem powierzchni . Figura posiadająca pole nazywa się do kwadratu .

Powierzchnia płaskiej figury pod względem geometrycznym

1. Kwadrat-miara figury płaskiej w stosunku do figury standardowej, jaką jest kwadrat o boku równym jednej jednostce długości.

2. Kwadrat- cecha liczbowa przypisana płaskim figurom określonej klasy (na przykład wielokątom). Pole kwadratu o boku równym jednostce długości, przyjmowane jako równe jednostce pola

3. Kwadrat- wielkość dodatnia, której wartość liczbowa ma następujące właściwości:

 Równe figury mają równe pola;

 Jeśli figura jest podzielona na części, które są figurami prostymi (to znaczy takimi, które można podzielić na skończoną liczbę płaskich trójkątów), wówczas pole tej figury jest równe sumie pól jej części;

 Pole kwadratu o boku równym jednej jednostce miary jest równe jeden.

Możemy zatem stwierdzić, że powierzchnia nie jest określoną wielkością, a jedynie daje pewną warunkową charakterystykę dowolnej płaskiej figury. Aby znaleźć obszar dowolnej figury, musisz określić, ile kwadratów o boku równym jednej jednostce długości zawiera. Weźmy na przykład prostokąt, w którym centymetr kwadratowy mieści się dokładnie 6 razy. Oznacza to, że pole prostokąta wynosi 6 cm 2.

Wybór pola kwadratu o boku równym jednostce miary jako minimalnej jednostki miary wszystkich pól nie jest przypadkowy. Jest to wynik porozumienia między ludźmi, które powstało w wyniku wielowiekowej „naturalnej” selekcji. Ponadto pojawiły się inne propozycje jednostki miary. Na przykład proponowano przyjąć jako taką jednostkę powierzchnię trójkąta równobocznego (tj. dowolną płaską figurę można przedstawić jako „sumę” pewnej liczby trójkątów równobocznych), co prowadziłoby do zmiana numerycznej reprezentacji obszarów.

Zatem wzory do obliczania obszarów pojawiły się w matematyce i nie zostały od razu zrealizowane przez człowieka - to wielu naukowców żyjących w różnych epokach i różnych krajach. (Niepoprawne formuły nie znalazły miejsca w nauce i poszły w zapomnienie). Prawdziwe formuły były uzupełniane, poprawiane i potwierdzane przez tysiące lat, aż dotarły do ​​nas w nowoczesnej postaci.

To samo pomiar powierzchni polega na porównaniu pola danej figury z polem figury przyjętym jako jednostka miary. W wyniku porównania otrzymuje się pewną liczbę – liczbową wartość pola danej figury. Liczba ta pokazuje, ile razy pole danej figury jest większe (lub mniejsze) od pola figury przyjętego jako jednostka pola.

T Możemy zatem stwierdzić, że pole jest sztuczną wielkością, historycznie wprowadzoną przez człowieka do pomiaru jakiejś właściwości płaskiej figury. Konieczność wpisania takiej wartości została podyktowana rosnącą potrzebą wiedzy o tym, jak duże jest dane terytorium, ile zboża potrzeba do obsiewania pola czy obliczenia powierzchni podłogi pod ułożenie płytek ozdobnych.

Wzór Picka

Aby oszacować powierzchnię wielokąta na papierze w kratkę, wystarczy policzyć, ile komórek obejmuje ten wielokąt (powierzchnię komórki przyjmujemy jako jeden). Dokładniej, jeśliS to powierzchnia wielokąta, B to liczba komórek znajdujących się całkowicie wewnątrz wielokąta, a G to liczba komórek, które mają wnętrze. Rozważymy tylko takie wielokąty, których wszystkie wierzchołki leżą w węzłach szachownicy - takie, w których linie siatki wielokątów przecinają się co najmniej w jednym punkcie wspólnym.

Pole dowolnego trójkąta narysowanego na papierze w kratkę można łatwo obliczyć, przedstawiając go jako sumę lub różnicę pól trójkątów prostokątnych i prostokątów, których boki podążają za liniami siatki przechodzącymi przez wierzchołki narysowanego trójkąta.

Aby obliczyć powierzchnię takiego wielokąta, możesz skorzystać z następującego twierdzenia:

Twierdzenie . Pozwalać - liczba punktów całkowitych wewnątrz wielokąta, - liczba punktów całkowitych na jego granicy, - jego obszar. Wtedy jest sprawiedliwieWzór Picka:

Przykład. Dla wielokąta na rysunkuL = 7 (czerwone kropki), 9 (zielone kropki) takS = 7+ 9/2 -1 = 10,5 jednostki kwadratowe.

Twierdzenie Picka- klasyczny wynik I .

Pole trójkąta z wierzchołkami w węzłach i niezawierającego żadnych węzłów ani wewnątrz, ani po bokach (z wyjątkiem wierzchołków) wynosi 1/2. Ten fakt.

3. Historia

Wzór Picka odkrył austriacki matematyk Georg Alexander (1859-1942). . W wieku 16 lat Georg ukończył szkołę i wstąpił do szkoły. W wieku 20 lat otrzymał uprawnienia do nauczania fizyki i matematyki. W 1884 Peake wyjechał do Do . Tam poznał kolejnego ucznia Kleina,. Później, w 1885 roku, powrócił do, gdzie spędził resztę swojej kariery naukowej.

Georg Pieck przyjaźnił się z Einsteinem. Peake i Einstein mieli nie tylko wspólne zainteresowania naukowe, ale także pasję do muzyki. Pick, który grał w kwartecie złożonym z profesorów uniwersyteckich, wprowadził Einsteina do towarzystw naukowych i muzycznych Pragi.

Zakres zainteresowań matematycznych Peake'a był niezwykle szeroki. W szczególności mają ponad 50 prac naukowych. Twierdzenie Picka o obliczaniu pola wielokąta, odkryte przez niego w 1899 roku, stało się powszechnie znane. W Niemczech twierdzenie to znajduje się w podręcznikach szkolnych.

4.Zastosowania formuły Picka

Wzór Picka służy nie tylko do obliczania pól wielokątów, ale także do rozwiązywania wielu problemów na poziomie olimpijskim.

Kilka przykładów wykorzystania formuły Pick przy rozwiązywaniu problemów:

1) Król szachowy chodził po planszy złożonej z komórek 8 × 8, odwiedzając każdą

pole domu dokładnie raz i ostatnim ruchem powracającym do oryginału

pole. Linia przerywana łącząca kolejno środki pól

minął króla, nie ma samoprzecięć. Jaki obszar może

ograniczyć tę przerywaną linię? (Bok komórki to 1.)

Ze wzoru Peaka od razu wynika, że ​​obszar ograniczony lo-

mana równa 64/2 - 1 = 31; tutaj węzły sieci są środkami 64

pola i pod warunkiem, że wszystkie leżą na granicy wielokąta. Więc

Tak więc, chociaż takich „trajektorii” króla jest sporo, to wszystkie są

związane wielokąty o równych polach.

Zadania z materiałów testowo-pomiarowych Państwowej Agencji Egzaminacyjnej i Jednolitego Egzaminu Państwowego

Zadanie B3

Znajdź obszar figury przedstawiony na papierze w kratkę o rozmiarze komórki 1 cm 1 cm (patrz rysunek). Podaj odpowiedź w centymetrach kwadratowych.

4.Wniosek

W trakcie badań zapoznawałem się z literaturą referencyjną i popularnonaukową. Dowiedziałem się, że problem znalezienia pola wielokąta z wierzchołkami w węzłach siatki skłonił austriackiego matematyka Piecka do udowodnienia niezwykłej formuły Piecka w 1899 roku.

W wyniku mojej pracy poszerzyłem swoją wiedzę na temat rozwiązywania problemów na papierze w kratkę, ustaliłem dla siebie klasyfikację badanych problemów i utwierdziłem się w ich różnorodności.

Nauczyłem się obliczać pola wielokątów narysowanych na kartce papieru w kratkę. Rozważane zadania mają różny stopień trudności – od prostych po olimpijskie. Każdy może znaleźć wśród nich zadania o możliwym do osiągnięcia poziomie złożoności, od których będzie można przejść do rozwiązywania trudniejszych.

Doszedłem do wniosku, że temat, który mnie interesował, był dość wieloaspektowy, problemy na papierze w kratkę były różnorodne, różne były też metody i techniki ich rozwiązywania. Dlatego postanowiliśmy kontynuować prace w tym kierunku.

5. Wykorzystana literatura:

1. Wasiljew N. B. Wokół formuły Pick // Quantum. - 1974. - nr 12

2. K o k e P r as o l o v V. V. Zagadnienia planimetrii. - M.: MTsNMO, 2006.t e r G.S.M. Wprowadzenie do geometrii. - M.: Nauka, 1966

3.Roslova L.O., Sharygin I.F. Pomiary. – M.: Wydawnictwo. „Otwarty świat”, 2005.

Zasoby internetowe:

:

Informacje zwrotne do pracy

„Obliczanie pól figur płaskich. Wybierz metodę”

Uwzględnienie tego tematu zwiększy aktywność poznawczą ucznia, który później zacznie dostrzegać harmonię rysunku na lekcjach geometrii i przestanie postrzegać geometrię (i w ogóle matematykę) jako nudną naukę.

Recenzowana przez nauczyciela matematyki

Chodyrewa Tatiana Georgiewna