Lekcja nr.2
Temat: Funkcja wykładnicza, jej własności i wykres.
Cel: Sprawdź jakość opanowania koncepcji „funkcji wykładniczej”; kształcenie umiejętności i umiejętności rozpoznawania funkcji wykładniczej, korzystania z jej własności i wykresów, nauczenie studentów posługiwania się analitycznymi i graficznymi formami zapisu funkcji wykładniczej; zapewnić środowisko pracy w klasie.
Sprzęt: tablica, plakaty
Formularz lekcji: lekcja klasowa
Typ lekcji: lekcja praktyczna
Typ lekcji: lekcja umiejętności i umiejętności nauczania
Plan lekcji
1. Moment organizacyjny
2. Samodzielna praca i sprawdzanie zadań domowych
3. Rozwiązywanie problemów
4. Podsumowanie
5. Praca domowa
Postęp lekcji.
1. Moment organizacyjny :
Cześć. Otwórz zeszyty, zapisz dzisiejszą datę i temat lekcji „Funkcja wykładnicza”. Dzisiaj będziemy kontynuować badanie funkcji wykładniczej, jej właściwości i wykresu.
2. Samodzielna praca i sprawdzanie zadań domowych .
Cel: sprawdź jakość opanowania pojęcia „funkcji wykładniczej” i sprawdź zaliczenie części teoretycznej pracy domowej
Metoda: zadanie testowe, badanie czołowe
Jako zadanie domowe otrzymaliście cyfry z zeszytu zadań i akapit z podręcznika. Nie będziemy teraz sprawdzać Twojego wykonania liczb z podręcznika, ale zeszyty oddasz na koniec lekcji. Teraz teoria zostanie sprawdzona w formie małego testu. Zadanie jest takie samo dla wszystkich: dostajesz listę funkcji, musisz dowiedzieć się, które z nich mają charakter orientacyjny (podkreśl je). A obok funkcji wykładniczej musisz napisać, czy rośnie, czy maleje.
Opcja 1 Odpowiedź B) D) - wykładniczy, malejący | Opcja 2 Odpowiedź D) - wykładniczy, malejący D) - wykładniczy, rosnący |
Opcja 3 Odpowiedź A) - wykładniczy, rosnący B) - wykładniczy, malejący | Opcja 4 Odpowiedź A) - wykładniczy, malejący W) - wykładniczy, rosnący |
Zapamiętajmy teraz wspólnie, która funkcja nazywa się wykładniczą?
Funkcja postaci , gdzie i nazywana jest funkcją wykładniczą.
Jaki jest zakres tej funkcji?
Wszystkie liczby rzeczywiste.
Jaki jest zakres funkcji wykładniczej?
Wszystkie dodatnie liczby rzeczywiste.
Zmniejsza się, jeśli podstawa potęgi jest większa od zera, ale mniejsza od jedności.
W jakim przypadku funkcja wykładnicza maleje w swojej dziedzinie definicji?
Zwiększanie, jeśli podstawa potęgi jest większa niż jeden.
3. Rozwiązywanie problemów
Cel: rozwinięcie umiejętności rozpoznawania funkcji wykładniczej, wykorzystania jej własności i wykresów, nauczenie studentów posługiwania się analitycznymi i graficznymi formami zapisu funkcji wykładniczej
Metoda: pokaz rozwiązywania typowych problemów przez nauczyciela, praca ustna, praca przy tablicy, praca w zeszycie, rozmowa nauczyciela z uczniami.
Właściwości funkcji wykładniczej można wykorzystać przy porównywaniu 2 lub więcej liczb. Na przykład: nr 000. Porównaj wartości i jeśli a) ![]() ..gif" szerokość="37" wysokość="20 src=">, to jest to dość skomplikowane zadanie: musielibyśmy wziąć pierwiastek sześcienny z 3 i 9 i porównać je. Wiemy jednak, że to rośnie, to na swój sposób oznacza, że wraz ze wzrostem argumentu wzrasta wartość funkcji, to znaczy wystarczy porównać wartości argumentu i , jest oczywiste, że
..gif" szerokość="37" wysokość="20 src=">, to jest to dość skomplikowane zadanie: musielibyśmy wziąć pierwiastek sześcienny z 3 i 9 i porównać je. Wiemy jednak, że to rośnie, to na swój sposób oznacza, że wraz ze wzrostem argumentu wzrasta wartość funkcji, to znaczy wystarczy porównać wartości argumentu i , jest oczywiste, że ![]() (można wykazać na plakacie przedstawiającym rosnącą funkcję wykładniczą). I zawsze, rozwiązując takie przykłady, najpierw określasz podstawę funkcji wykładniczej, porównujesz ją z 1, określasz monotoniczność i przystępujesz do porównywania argumentów. W przypadku funkcji malejącej: gdy argument rośnie, wartość funkcji maleje, dlatego przy przejściu od nierówności argumentów do nierówności funkcji zmieniamy znak nierówności. Następnie rozwiązujemy ustnie: b)
(można wykazać na plakacie przedstawiającym rosnącą funkcję wykładniczą). I zawsze, rozwiązując takie przykłady, najpierw określasz podstawę funkcji wykładniczej, porównujesz ją z 1, określasz monotoniczność i przystępujesz do porównywania argumentów. W przypadku funkcji malejącej: gdy argument rośnie, wartość funkcji maleje, dlatego przy przejściu od nierówności argumentów do nierówności funkcji zmieniamy znak nierówności. Następnie rozwiązujemy ustnie: b) ![]()
- ![]()
W) ![]()
- ![]()
G) ![]()
- ![]()
- Nr 000. Porównaj liczby: a) i

Zatem funkcja rośnie
Dlaczego ?
Zwiększanie funkcji i ![]()
Zatem funkcja jest malejąca ![]()
Obie funkcje rosną w całej swojej dziedzinie definicji, ponieważ są wykładnicze z podstawą potęgi większą niż jeden.
Jakie kryje się za tym znaczenie?
Budujemy wykresy:

Która funkcja rośnie szybciej podczas wysiłku https://pandia.ru/text/80/379/images/image062_0.gif" szerokość="20 wysokość=25" wysokość="25">
Która funkcja maleje szybciej podczas wysiłku https://pandia.ru/text/80/379/images/image062_0.gif" szerokość="20 wysokość=25" wysokość="25">
Która z funkcji ma w danym punkcie większą wartość na przedziale?
D), https://pandia.ru/text/80/379/images/image068_0.gif" szerokość="69" wysokość="57 src=">. Najpierw poznajmy zakres definicji tych funkcji. Czy pokrywają się?
Tak, dziedziną tych funkcji są wszystkie liczby rzeczywiste.
Nazwij zakres każdej z tych funkcji.
Zakresy tych funkcji pokrywają się: wszystkie dodatnie liczby rzeczywiste.
Określ rodzaj monotoniczności każdej funkcji.
Wszystkie trzy funkcje maleją w całej dziedzinie definicji, ponieważ są wykładnicze o podstawie potęg mniejszej niż jeden i większej niż zero.
Jaki specjalny punkt istnieje na wykresie funkcji wykładniczej?
Jakie kryje się za tym znaczenie?
Niezależnie od podstawy stopnia funkcji wykładniczej, jeśli wykładnik zawiera 0, wówczas wartość tej funkcji wynosi 1.
Budujemy wykresy:

Przeanalizujmy wykresy. Ile punktów przecięcia mają wykresy funkcji?
Która funkcja maleje szybciej podczas wysiłku https://pandia.ru/text/80/379/images/image070.gif" szerokość="41 wysokość=57" wysokość="57">
Która funkcja rośnie szybciej podczas wysiłku https://pandia.ru/text/80/379/images/image070.gif" szerokość="41 wysokość=57" wysokość="57">
Która z funkcji ma w danym punkcie większą wartość na przedziale?
Która z funkcji ma w danym punkcie większą wartość na przedziale?
Dlaczego funkcje wykładnicze o różnych podstawach mają tylko jeden punkt przecięcia?
Funkcje wykładnicze są ściśle monotoniczne w całej swojej dziedzinie definicji, więc mogą przecinać się tylko w jednym punkcie.
Następne zadanie skupi się na wykorzystaniu tej właściwości. Nr 000. Znajdź największą i najmniejszą wartość danej funkcji w danym przedziale a) . Przypomnijmy, że funkcja ściśle monotoniczna przyjmuje wartości minimalne i maksymalne na końcach danego odcinka. A jeśli funkcja jest rosnąca, to jej największa wartość będzie na prawym końcu odcinka, a najmniejsza na lewym końcu odcinka (pokaz na plakacie na przykładzie funkcji wykładniczej). Jeżeli funkcja maleje, to jej największa wartość będzie na lewym końcu odcinka, a najmniejsza na prawym końcu odcinka (pokaz na plakacie na przykładzie funkcji wykładniczej). Funkcja rośnie, ponieważ zatem najmniejsza wartość funkcji będzie w punkcie https://pandia.ru/text/80/379/images/image075_0.gif" szerokość="145" wysokość="29" >. Punkty b)  , V)
, V)  d) samodzielnie rozwiąż zeszyty, my sprawdzimy je ustnie.
d) samodzielnie rozwiąż zeszyty, my sprawdzimy je ustnie.
Uczniowie rozwiązują zadanie w swoich zeszytach
|
Funkcja malejąca
|
Funkcja malejąca
|
Funkcja rosnąca
|
- nr 000. Znajdź największą i najmniejszą wartość danej funkcji w podanym przedziale a) ![]() . To zadanie jest prawie takie samo jak poprzednie. Ale tutaj nie jest podany odcinek, ale promień. Wiemy, że funkcja jest rosnąca i nie ma ani największej, ani najmniejszej wartości na całej osi liczbowej https://pandia.ru/text/80/379/images/image063_0.gif" szerokość="68" wysokość = "20">, i dąży do , czyli na półprostej funkcja at dąży do 0, ale nie ma najmniejszej wartości, ale największą wartość ma w punkcie
. To zadanie jest prawie takie samo jak poprzednie. Ale tutaj nie jest podany odcinek, ale promień. Wiemy, że funkcja jest rosnąca i nie ma ani największej, ani najmniejszej wartości na całej osi liczbowej https://pandia.ru/text/80/379/images/image063_0.gif" szerokość="68" wysokość = "20">, i dąży do , czyli na półprostej funkcja at dąży do 0, ale nie ma najmniejszej wartości, ale największą wartość ma w punkcie ![]() . Punkty b)
. Punkty b)  , V)
, V) ![]() , G)
, G)  rozwiąż samodzielnie zeszyty, my sprawdzimy je ustnie.
rozwiąż samodzielnie zeszyty, my sprawdzimy je ustnie.
1. Funkcja wykładnicza jest funkcją postaci y(x) = a x, w zależności od wykładnika x, o stałej wartości podstawy stopnia a, gdzie a > 0, a ≠ 0, xϵR (R jest zbiór liczb rzeczywistych).
Rozważmy wykres funkcji jeśli podstawa nie spełnia warunku: a>0
a)< 0
Jeśli< 0 – возможно возведение в целую степень или в рациональную степень с нечетным показателем.
a = -2

Jeśli a = 0, funkcja y = jest zdefiniowana i ma stałą wartość 0

c) a =1
Jeśli a = 1, funkcja y = jest zdefiniowana i ma stałą wartość 1
Domena funkcji (DOF) Zakres dopuszczalnych wartości funkcji (APV) 3. Zera funkcji (y = 0) 4. Punkty przecięcia z osią rzędnych oy (x = 0) 5. Funkcje rosnące, malejące Jeśli , to funkcja f(x) rośnie 6. Funkcja parzysta, nieparzysta Funkcja y = nie jest symetryczna względem osi 0y i względem początku współrzędnych, zatem nie jest ani parzysta, ani nieparzysta. (Funkcja ogólna) 7. Funkcja y = nie ma ekstremów 8. Właściwości stopnia z wykładnikiem rzeczywistym: Niech a > 0; a≠1 Następnie dla xϵR; tyR: Właściwości stopnia monotoniczności: jeśli, to Jeśli a > 0, to . 9. Względne położenie funkcji Im większa podstawa a, tym bliżej osi x i oy a > 1, a = 20 Przykład 1. Rozwiązanie większości problemów matematycznych w taki czy inny sposób polega na przekształcaniu wyrażeń numerycznych, algebraicznych lub funkcjonalnych. Powyższe dotyczy w szczególności decyzji. W wersjach Unified State Exam z matematyki do tego typu zadania zalicza się w szczególności zadanie C3. Nauka rozwiązywania zadań C3 jest ważna nie tylko po to, aby pomyślnie zdać egzamin Unified State Exam, ale także dlatego, że umiejętność ta przyda się podczas nauki matematyki w szkole średniej. Wykonując zadania C3 trzeba rozwiązywać różnego rodzaju równania i nierówności. Należą do nich racjonalne, irracjonalne, wykładnicze, logarytmiczne, trygonometryczne, zawierające moduły (wartości bezwzględne), a także połączone. W artykule omówiono główne typy równań i nierówności wykładniczych, a także różne metody ich rozwiązywania. O rozwiązywaniu innych typów równań i nierówności przeczytasz w dziale „” w artykułach poświęconych metodom rozwiązywania problemów C3 z Unified State Examination z matematyki. Zanim zaczniemy analizować konkretne Równania i nierówności wykładnicze Jako korepetytor matematyki sugeruję, abyś odświeżył trochę materiału teoretycznego, który będzie nam potrzebny. Funkcja formy y = x, Gdzie A> 0 i A≠ 1 nazywa się funkcja wykładnicza. Podstawowy własności funkcji wykładniczej y = x: Wykres funkcji wykładniczej to wykładnik potęgowy: Wykresy funkcji wykładniczych (wykładniki) Orientacyjny nazywane są równaniami, w których nieznana zmienna występuje tylko w wykładnikach niektórych potęg. Aby rozwiązać równania wykładnicze musisz znać i umieć zastosować następujące proste twierdzenie: Twierdzenie 1. Równanie wykładnicze A F(X) = A G(X) (Gdzie A > 0, A≠ 1) jest równoważne równaniu F(X) = G(X). Ponadto warto zapamiętać podstawowe formuły i operacje na stopniach: Title="Wyrenderowane przez QuickLaTeX.com">!} Przykład 1. Rozwiąż równanie: Rozwiązanie: Korzystamy z powyższych wzorów i podstawień: Równanie staje się wówczas: Dyskryminator otrzymanego równania kwadratowego jest dodatni: Title="Wyrenderowane przez QuickLaTeX.com">!} Oznacza to, że to równanie ma dwa pierwiastki. Znajdujemy je: Przechodząc do odwrotnego podstawienia, otrzymujemy: Drugie równanie nie ma pierwiastków, ponieważ funkcja wykładnicza jest ściśle dodatnia w całej dziedzinie definicji. Rozwiążmy drugie: Biorąc pod uwagę to, co zostało powiedziane w Twierdzeniu 1, przechodzimy do równoważnego równania: X= 3. To będzie odpowiedź na zadanie. Odpowiedź: X = 3. Przykład 2. Rozwiąż równanie: Rozwiązanie: Równanie nie ma ograniczeń co do zakresu dopuszczalnych wartości, ponieważ wyrażenie radykalne ma sens dla dowolnej wartości X(funkcja wykładnicza y = 9 4 -X dodatnia i różna od zera). Równanie rozwiązujemy za pomocą przekształceń równoważnych, korzystając z zasad mnożenia i dzielenia potęg: Ostatnie przejście przeprowadzono zgodnie z Twierdzeniem 1. Odpowiedź:X= 6.
Przykład 3. Rozwiąż równanie: Rozwiązanie: obie strony pierwotnego równania można podzielić przez 0,2 X. To przejście będzie równoważne, ponieważ to wyrażenie jest większe od zera dla dowolnej wartości X(funkcja wykładnicza jest ściśle dodatnia w swojej dziedzinie definicji). Wtedy równanie przyjmuje postać: Odpowiedź: X = 0. Przykład 4. Rozwiąż równanie: Rozwiązanie: upraszczamy równanie do elementarnego poprzez przekształcenia równoważne, korzystając z podanych na początku artykułu zasad dzielenia i mnożenia potęg: Dzielenie obu stron równania przez 4 X, jak w poprzednim przykładzie, jest równoważną transformacją, ponieważ to wyrażenie nie jest równe zero dla żadnej wartości X. Odpowiedź: X = 0. Przykład 5. Rozwiąż równanie: Rozwiązanie: funkcjonować y = 3X, stojąca po lewej stronie równania, rośnie. Funkcjonować y = —X Wartość -2/3 po prawej stronie równania maleje. Oznacza to, że jeśli wykresy tych funkcji przecinają się, to co najwyżej w jednym punkcie. W tym przypadku łatwo zgadnąć, że wykresy przecinają się w tym punkcie X= -1. Innych korzeni nie będzie. Odpowiedź: X = -1. Przykład 6. Rozwiąż równanie: Rozwiązanie: upraszczamy równanie za pomocą przekształceń równoważnych, pamiętając wszędzie, że funkcja wykładnicza jest ściśle większa od zera dla dowolnej wartości X i korzystając z zasad obliczania iloczynu i ilorazu potęg podanych na początku artykułu: Odpowiedź: X = 2. Orientacyjny nazywane są nierównościami, w których nieznana zmienna jest zawarta tylko w wykładnikach niektórych potęg. Aby rozwiązać nierówności wykładnicze wymagana jest znajomość następującego twierdzenia: Twierdzenie 2. Jeśli A> 1, to nierówność A F(X) > A G(X) jest równoważne nierówności o tym samym znaczeniu: F(X) > G(X). Jeśli 0< A < 1, то показательное неравенство A F(X) > A G(X) jest równoważne nierówności o odwrotnym znaczeniu: F(X) < G(X). Przykład 7. Rozwiąż nierówność: Rozwiązanie: Przedstawiamy pierwotną nierówność w postaci: Podzielmy obie strony tej nierówności przez 3 2 X, w tym przypadku (ze względu na dodatniość funkcji y= 3 2X) znak nierówności nie ulegnie zmianie: Skorzystajmy z podstawienia: Wtedy nierówność będzie miała postać: Zatem rozwiązaniem nierówności jest przedział: przechodząc do odwrotnego podstawienia, otrzymujemy: Ze względu na dodatniość funkcji wykładniczej lewa nierówność jest spełniona automatycznie. Korzystając ze znanej własności logarytmu, przechodzimy do równoważnej nierówności: Ponieważ podstawa stopnia jest liczbą większą niż jeden, równoważne (zgodnie z Twierdzeniem 2) jest przejście do następującej nierówności: Więc w końcu dostajemy odpowiedź: Przykład 8. Rozwiąż nierówność: Rozwiązanie: Korzystając z własności mnożenia i dzielenia potęg, zapisujemy nierówność w postaci: Wprowadźmy nową zmienną: Uwzględniając to podstawienie, nierówność przyjmuje postać: Mnożąc licznik i mianownik ułamka przez 7, otrzymujemy równoważną nierówność: Zatem następujące wartości zmiennej spełniają nierówność T: Następnie przechodząc do odwrotnego podstawienia otrzymujemy: Ponieważ podstawa stopnia jest tutaj większa niż jeden, przejście do nierówności będzie równoważne (zgodnie z Twierdzeniem 2): Wreszcie dostajemy odpowiedź: Przykład 9. Rozwiąż nierówność: Rozwiązanie: Obie strony nierówności dzielimy według wyrażenia: Jest ona zawsze większa od zera (ze względu na dodatniość funkcji wykładniczej), więc znaku nierówności nie trzeba zmieniać. Otrzymujemy: t znajdujący się w przedziale: Przechodząc do odwrotnego podstawienia, okazuje się, że pierwotna nierówność dzieli się na dwa przypadki: Pierwsza nierówność nie ma rozwiązań ze względu na dodatniość funkcji wykładniczej. Rozwiążmy drugie: Przykład 10. Rozwiąż nierówność: Rozwiązanie: Gałęzie paraboli y = 2X+2-X 2 są skierowane w dół, dlatego jest ograniczona od góry wartością, jaką osiąga na swoim wierzchołku: Gałęzie paraboli y = X 2 -2X+2 we wskaźniku są skierowane w górę, co oznacza, że jest on ograniczony od dołu wartością, jaką osiąga na swoim wierzchołku: Jednocześnie funkcja okazuje się również ograniczona od dołu y = 3 X 2 -2X+2, co jest po prawej stronie równania. Najmniejszą wartość osiąga w tym samym punkcie, co parabola wykładnika, a wartość ta wynosi 3 1 = 3. Zatem pierwotna nierówność może być prawdziwa tylko wtedy, gdy funkcja po lewej stronie i funkcja po prawej stronie przyjmą wartość , równy 3 (przecięciem zakresów wartości tych funkcji jest tylko ta liczba). Warunek ten jest spełniony w jednym punkcie X = 1. Odpowiedź: X= 1. Aby nauczyć się decydować równania i nierówności wykładnicze, konieczne jest ciągłe szkolenie w ich rozwiązywaniu. W tym trudnym zadaniu pomogą Ci różnorodne pomoce dydaktyczne, zeszyty zadań z matematyki elementarnej, zbiory zadań konkursowych, zajęcia z matematyki w szkole, a także lekcje indywidualne z profesjonalnym korepetytorem. Serdecznie życzę sukcesów w przygotowaniach i doskonałych wyników na egzaminie. P.S. Drodzy Goście! Proszę nie pisać w komentarzach próśb o rozwiązanie równań. Niestety nie mam na to kompletnie czasu. Takie wiadomości będą usuwane. Proszę przeczytać artykuł. Być może znajdziesz w nim odpowiedzi na pytania, które nie pozwoliły Ci samodzielnie rozwiązać zadania. Wprowadźmy najpierw definicję funkcji wykładniczej. Funkcja wykładnicza $f\lewo(x\prawo)=a^x$, gdzie $a >1$. Przedstawmy własności funkcji wykładniczej dla $a >1$. \ \[bez korzeni\] \ Przecięcie z osiami współrzędnych. Funkcja nie przecina osi $Ox$, ale przecina oś $Oy$ w punkcie $(0,1)$. $f""\lewo(x\prawo)=(\lewo(a^xlna\prawo))"=a^x(ln)^2a$ \ \[bez korzeni\] \ Wykres (ryc. 1). Rysunek 1. Wykres funkcji $f\left(x\right)=a^x,\ for\ a >1$. Przedstawmy właściwości funkcji wykładniczej przy wartości 0 $ Dziedziną definicji są wszystkie liczby rzeczywiste. $f\left(-x\right)=a^(-x)=\frac(1)(a^x)$ -- funkcja nie jest ani parzysta, ani nieparzysta. $f(x)$ jest ciągłe w całym obszarze definicji. Zakres wartości to przedział $(0,+\infty)$. $f"(x)=\lewo(a^x\prawo)"=a^xlna$ \ \[bez korzeni\] \ \[bez korzeni\] \ Funkcja jest wypukła w całej dziedzinie definicji. Zachowanie na końcach domeny: \[(\mathop(lim)_(x\to -\infty ) a^x\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) a^x\ ) =0\] Wykres (ryc. 2). Zbadaj i wykreśl funkcję $y=2^x+3$. Rozwiązanie. Przeprowadźmy badanie, korzystając z powyższego przykładowego diagramu: Dziedziną definicji są wszystkie liczby rzeczywiste. $f\left(-x\right)=2^(-x)+3$ -- funkcja nie jest ani parzysta, ani nieparzysta. $f(x)$ jest ciągłe w całym obszarze definicji. Zakres wartości to przedział $(3,+\infty)$. $f"\lewo(x\prawo)=(\lewo(2^x+3\prawo))"=2^xln2>0$ Funkcja rośnie w całym obszarze definicji. $f(x)\ge 0$ w całym obszarze definicji. Przecięcie z osiami współrzędnych. Funkcja nie przecina osi $Ox$, ale przecina oś $Oy$ w punkcie ($0,4)$ $f""\lewo(x\prawo)=(\lewo(2^xln2\prawo))"=2^x(ln)^22>0$ Funkcja jest wypukła w całej dziedzinie definicji. Zachowanie na końcach domeny: \[(\mathop(lim)_(x\to -\infty ) a^x\ )=0\] \[(\mathop(lim)_(x\to +\infty ) a^x\ )=+ \infty\] Wykres (ryc. 3). Rysunek 3. Wykres funkcji $f\left(x\right)=2^x+3$ Hipermarket wiedzy >>Matematyka >>Matematyka 10 klasa >> Funkcja wykładnicza, jej własności i wykres Rozważmy wyrażenie 2x i znajdź jego wartości dla różnych wymiernych wartości zmiennej x, na przykład dla x = 2; Ogólnie rzecz biorąc, niezależnie od tego, jakie racjonalne znaczenie przypiszemy zmiennej x, zawsze możemy obliczyć odpowiadającą jej wartość liczbową wyrażenia 2 x. Można więc mówić o wykładniczym funkcje y=2 x, określone na zbiorze Q liczb wymiernych: Przyjrzyjmy się niektórym właściwościom tej funkcji. Właściwość 1.- funkcja rosnąca. Dowód przeprowadzamy w dwóch etapach. Po lewej stronie ostatniej nierówności mamy , a po prawej stronie 1. Oznacza to, że ostatnią nierówność można zapisać w postaci Drugi etap. Niech x 1 i x 2 będą liczbami, a x 1 i x 2< х2. Составим разность 2 х2 -2 х1 и выполним некоторые ее преобразования: (różnicę x 2 - x 1 oznaczyliśmy literą r). Ponieważ r jest dodatnią liczbą wymierną, to zgodnie z tym, co udowodniono na pierwszym etapie, 2 r > 1, tj. 2 r -1 >0. Liczba 2x" jest również dodatnia, co oznacza, że iloczyn 2 x-1 (2· -1) również jest dodatni. W ten sposób udowodniliśmy, że nierówność 2Xg -2x" >0. Zatem z nierówności x 1< х 2 следует, что 2х" <2 x2 , а это и означает, что функция у -2х - возрастающая. Własność 2. ograniczone od dołu i nie ograniczone od góry. To, że funkcja ta nie jest najważniejsza, jest oczywiste, ponieważ, jak właśnie widzieliśmy, nie jest ona ograniczona powyżej. Ale jest ograniczona od dołu, dlaczego nie ma wartości minimalnej? Załóżmy, że 2 r jest najmniejszą wartością funkcji (r jest jakimś wymiernym wskaźnikiem). Weźmy liczbę wymierną q<г. Тогда в силу возрастания функции у=2 х будем иметь 2 x <2г. А это значит, что 2 r не может служить наименьшим значением функции. Wszystko to dobrze, mówisz, ale dlaczego funkcji y-2 x rozważamy tylko na zbiorze liczb wymiernych, dlaczego nie rozważamy jej jak innych znanych funkcji na całej osi liczbowej lub na jakimś ciągłym przedziale liczby oś liczbowa? Co nas powstrzymuje? Zastanówmy się nad sytuacją. Oś liczbowa zawiera nie tylko liczby wymierne, ale także liczby niewymierne. W przypadku wcześniej badanych funkcji nie przeszkadzało nam to. Na przykład równie łatwo znaleźliśmy wartości funkcji y = x2 zarówno dla wymiernych, jak i niewymiernych wartości x: wystarczyło podnieść podaną wartość x do kwadratu. Ale w przypadku funkcji y=2 x sytuacja jest bardziej skomplikowana. Jeżeli argumentowi x nadajemy racjonalne znaczenie, to w zasadzie x można obliczyć (wróćmy jeszcze raz na początek akapitu, gdzie dokładnie to zrobiliśmy). Co się stanie, jeśli argument x otrzyma irracjonalne znaczenie? Jak na przykład obliczyć? Tego jeszcze nie wiemy. Wiadomo, że 1; 1,7; 1,73; 1,732; 1,7320; 1,73205; 1,732050; 1,7320508;... . Oczywiste jest, że 1,732 = 1,7320, a 1,732050 = 1,73205. Aby uniknąć takich powtórzeń, odrzucamy te elementy sekwencji, które kończą się liczbą 0. Otrzymujemy wówczas ciąg rosnący: 1; 1,7; 1,73; 1,732; 1,73205; 1,7320508;... . W związku z tym sekwencja wzrasta Wszystkie wyrazy tego ciągu są liczbami dodatnimi mniejszymi niż 22, tj. ta kolejność jest ograniczona. Zgodnie z twierdzeniem Weierstrassa (patrz § 30), jeśli ciąg jest rosnący i ograniczony, to jest zbieżny. Ponadto z § 30 wiemy, że jeśli ciąg jest zbieżny, to tylko do jednej granicy. Uzgodniono, że tę pojedynczą granicę należy traktować jako wartość wyrażenia liczbowego. I nie ma znaczenia, że bardzo trudno jest znaleźć nawet przybliżoną wartość wyrażenia liczbowego 2; ważne, żeby to była konkretna liczba (w końcu nie baliśmy się powiedzieć, że to na przykład pierwiastek równania wymiernego, Zaznaczmy punkty na płaszczyźnie współrzędnych (ryc. 194), zaznaczymy określoną linię, narysujmy ją (ryc. 195). Rygorystyczne dowody wymienionych własności funkcji y-2 x podaje się w toku matematyki wyższej. Niektóre z tych właściwości w mniejszym lub większym stopniu omawialiśmy wcześniej, niektóre z nich wyraźnie widać na skonstruowanym wykresie (patrz ryc. 195). Na przykład brak parzystości lub nieparzystości funkcji jest geometrycznie powiązany z brakiem symetrii wykresu odpowiednio względem osi y lub względem początku układu współrzędnych. Dowolna funkcja postaci y = a x, gdzie a > 1, ma podobne właściwości. Na ryc. Skonstruowano 196 w jednym układzie współrzędnych, wykresy funkcji y=2 x, y=3 x, y=5 x. Rozważmy teraz funkcję i utwórz dla niej tabelę wartości: 1) Definicja. Funkcja postaci nazywana jest funkcją wykładniczą. Wykres funkcji y=a x dla a > 1 pokazano na rys. 201 i dla 0<а < 1 - на рис. 202. Krzywa pokazana na ryc. Liczba 201 lub 202 nazywana jest wykładnikiem. W rzeczywistości matematycy zwykle nazywają samą funkcję wykładniczą y = a x. Zatem terminu „wykładnik” używa się w dwojakim znaczeniu: zarówno do nazwania funkcji wykładniczej, jak i do nazwania wykresu funkcji wykładniczej. Zwykle znaczenie jest jasne, czy mówimy o funkcji wykładniczej, czy o jej wykresie. Zwróć uwagę na cechę geometryczną wykresu funkcji wykładniczej y=ax: oś x jest asymptotą poziomą wykresu. To prawda, że to stwierdzenie jest zwykle wyjaśniane w następujący sposób. Innymi słowy To są przykłady funkcji potęgowych; Generalnie y = x r, gdzie r jest określoną liczbą, jest funkcją potęgową (argument x zawarty jest w podstawie stopnia); Funkcja „egzotyczna”, taka jak y = x”, nie jest uważana ani za wykładniczą, ani za potęgową (czasami nazywa się ją wykładniczą). Druga ważna uwaga. Zwykle nie rozważa się funkcji wykładniczej o podstawie a = 1 lub o podstawie a spełniającej nierówność a<0 (вы, конечно, помните, что выше, в определении показательной функции, оговорены условия: а >0 i a Faktem jest, że jeśli a = 1, to dla dowolnej wartości x zachodzi równość Ix = 1. Zatem funkcja wykładnicza y = a” przy a = 1 „degeneruje się” do funkcji stałej y = 1 – to. nie jest interesujące, jeśli a = 0, to 0x = 0 dla dowolnej dodatniej wartości x, czyli otrzymujemy funkcję y = 0, określoną dla x > 0 - to też jest nieciekawe. Jeśli w końcu a.<0, то выражение а" имеет смысл лишь при целых значениях х, а мы все-таки предпочитаем рассматривать функции, определенные на сплошных промежутках. Zanim przejdziesz do rozwiązywania przykładów, zwróć uwagę, że funkcja wykładnicza znacznie różni się od wszystkich funkcji, które do tej pory badałeś. Aby dokładnie przestudiować nowy obiekt, należy rozważyć go pod różnymi kątami, w różnych sytuacjach, więc będzie wiele przykładów. Rozwiązanie, a) Konstruując wykresy funkcji y = 2 x i y = 1 w jednym układzie współrzędnych zauważamy (ryc. 203), że mają one jeden punkt wspólny (0; 1). Oznacza to, że równanie 2x = 1 ma pojedynczy pierwiastek x =0. Zatem z równania 2x = 2° otrzymujemy x = 0. b) Konstruując wykresy funkcji y = 2 x i y = 4 w jednym układzie współrzędnych zauważamy (ryc. 203), że mają one jeden punkt wspólny (2; 4). Oznacza to, że równanie 2x = 4 ma pojedynczy pierwiastek x = 2. Zatem z równania 2 x = 2 2 otrzymujemy x = 2. c) i d) Na podstawie tych samych rozważań dochodzimy do wniosku, że równanie 2 x = 8 ma jeden pierwiastek i aby go znaleźć, nie trzeba budować wykresów odpowiednich funkcji; jasne jest, że x = 3, ponieważ 2 · 3 = 8. Podobnie znajdujemy jedyny pierwiastek równania Rozwiązanie. Możesz postępować w ten sposób: zbuduj wykres funkcji y-3 x, następnie rozciągnij go od osi x 3-krotnie, a następnie podnieś powstały wykres w górę o 2 jednostki skali. Ale wygodniej jest skorzystać z faktu, że 3- 3* = 3 * + 1 i dlatego zbudować wykres funkcji y = 3 x * 1 + 2. Przejdźmy dalej, jak to robiliśmy wielokrotnie w takich przypadkach, do pomocniczego układu współrzędnych z początkiem w punkcie (-1; 2) - linie kropkowane x = - 1 i 1x = 2 na ryc. 207. „Połączmy” funkcję y=3* z nowym układem współrzędnych. W tym celu należy wybrać punkty kontrolne dla funkcji Przykład 4. Rozwiąż równania i nierówności: Rozwiązanie, a) Skonstruujmy wykresy funkcji y=5* i y=6-x w jednym układzie współrzędnych (rys. 208). Przecinają się w jednym punkcie; sądząc po rysunku jest to punkt (1; 5). Kontrola pokazuje, że faktycznie punkt (1; 5) spełnia zarówno równanie y = 5*, jak i równanie y = 6-x. Odcięta tego punktu służy jako jedyny pierwiastek danego równania. Zatem równanie 5 x = 6 - x ma pojedynczy pierwiastek x = 1. b) i c) Wykładnik y-5x leży powyżej prostej y=6-x, jeśli x>1, widać to wyraźnie na rys. 208. Oznacza to, że rozwiązanie nierówności 5*>6 można zapisać następująco: x>1. I rozwiązanie nierówności 5x<6 - х можно записать так: х < 1. Przykład 5. Biorąc pod uwagę funkcję 
2. Przyjrzyjmy się bliżej funkcji wykładniczej:
0


Jeżeli , to funkcja f(x) maleje
Funkcja y= , przy 0
Wynika to z właściwości monotoniczności potęgi o wykładniku rzeczywistym.
b> 0; b≠1
Na przykład:


Funkcja wykładnicza jest ciągła w dowolnym punkcie ϵ R.


Jeśli a0, to funkcja wykładnicza przyjmuje postać bliską y = 0.
Jeżeli a1, to dalej od osi wół i oy i wykres przyjmuje postać zbliżoną do funkcji y = 1.
Skonstruuj wykres y =
Funkcja wykładnicza
Co to jest funkcja wykładnicza?
Wykres funkcji wykładniczej
Rozwiązywanie równań wykładniczych

![]()

![]()
![]()
![]()
![]()
Rozwiązywanie nierówności wykładniczych

![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
Siergiej Waleriewicz
Funkcja wykładnicza $f\lewo(x\prawo)=a^x$, gdzie $0
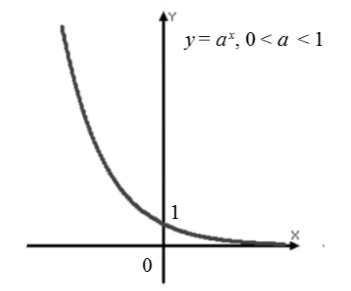
Przykład zadania konstrukcji funkcji wykładniczej

Pierwszy etap. Udowodnimy, że jeśli r jest dodatnią liczbą wymierną, to 2 r >1.
Możliwe są dwa przypadki: 1) r jest liczbą naturalną, r = n; 2) zwykłe nieredukowalne frakcja, 
Zatem w każdym przypadku zachodzi nierówność 2 r > 1 i właśnie to należało udowodnić.
Ograniczenie funkcji od dołu wynika z nierówności 2 x >0, która obowiązuje dla dowolnych wartości x z dziedziny definicji funkcji. Jednocześnie niezależnie od tego, jaką liczbę dodatnią M wybierzesz, zawsze możesz wybrać wykładnik x taki, że będzie spełniona nierówność 2 x >M - co charakteryzuje nieograniczoność funkcji z góry. Podajmy kilka przykładów. 
Własność 3. nie ma ani najmniejszej, ani największej wartości.
Matematycy znaleźli wyjście; tak rozumowali.![]() Rozważ sekwencję liczb wymiernych - dziesiętne przybliżenia liczby ze względu na wadę:
Rozważ sekwencję liczb wymiernych - dziesiętne przybliżenia liczby ze względu na wadę:![]() pierwiastek równania trygonometrycznego, bez zastanowienia się, czym dokładnie są te liczby:
pierwiastek równania trygonometrycznego, bez zastanowienia się, czym dokładnie są te liczby: ![]()
Dowiedzieliśmy się więc, jakie znaczenie matematycy nadają symbolowi 2^. Podobnie możesz określić, czym i ogólnie czym jest a, gdzie a jest liczbą niewymierną, a a > 1.
Ale co jeśli 0<а <1? Как вычислить, например, ? Самым естественным способом: считать, что свести вычисления к случаю, когда основание степени больше 1.
Teraz możemy mówić nie tylko o potęgach o dowolnych wykładnikach wymiernych, ale także o potęgach o dowolnych wykładnikach rzeczywistych. Udowodniono, że stopnie z dowolnymi wykładnikami rzeczywistymi mają wszystkie zwykłe właściwości stopni: przy mnożeniu potęg o tych samych podstawach wykładniki są dodawane, przy dzieleniu odejmuje się je, przy podnoszeniu stopnia do potęgi mnoży się, itp. Ale najważniejsze jest to, że teraz możemy mówić o funkcji y-ax określonej na zbiorze wszystkich liczb rzeczywistych.
Wróćmy do funkcji y = 2 x i skonstruujmy jej wykres. W tym celu utwórzmy tabelę wartości funkcji y=2x:

Własności funkcji y - 2 x:
1)
2) nie jest ani parzysty, ani nieparzysty; 248
3) podwyżki;
5) nie ma ani największej, ani najmniejszej wartości;
6) ciągły;
7)
8) wypukły w dół.
Zaznaczmy punkty na płaszczyźnie współrzędnych (ryc. 197), zaznaczymy określoną linię, narysujmy ją (ryc. 198).
Właściwości funkcji
2) nie jest ani parzysty, ani nieparzysty;
3) maleje;
4) nieograniczony od góry, ograniczony od dołu;
5) nie ma wartości największej ani najmniejszej;
6) ciągły;
7)
8) wypukły w dół.
Dowolna funkcja postaci y = a x ma podobne właściwości, gdzie O<а <1. На рис. 200 в одной системе координат построены графики функций ![]()
Uwaga: wykresy funkcji ![]() te. y=2 x, symetrycznie względem osi y (ryc. 201). Jest to konsekwencja twierdzenia ogólnego (patrz § 13): wykresy funkcji y = f(x) i y = f(-x) są symetryczne względem osi y. Podobnie wykresy funkcji y = 3 x i
te. y=2 x, symetrycznie względem osi y (ryc. 201). Jest to konsekwencja twierdzenia ogólnego (patrz § 13): wykresy funkcji y = f(x) i y = f(-x) są symetryczne względem osi y. Podobnie wykresy funkcji y = 3 x i
Podsumowując to, co zostało powiedziane, podamy definicję funkcji wykładniczej i podkreślimy jej najważniejsze właściwości.
Podstawowe własności funkcji wykładniczej y = a x
Oś x jest poziomą asymptotą wykresu funkcji

Pierwsza ważna uwaga. Uczniowie często mylą pojęcia: funkcja potęgowa, funkcja wykładnicza. Porównywać:![]()
To są przykłady funkcji wykładniczych.
y = a”, gdzie a jest określoną liczbą (dodatnią i różną od 1), jest funkcją wykładniczą (argument x zawarty jest w wykładniku).
Przykład 1. 
Zatem z równania 2x = 2 3 otrzymaliśmy x = 3, a z równania 2 x = 2 x otrzymaliśmy x = -4.
e) Wykres funkcji y = 2 x znajduje się nad wykresem funkcji y = 1 dla x > 0 - widać to wyraźnie na ryc. 203. Oznacza to, że rozwiązaniem nierówności 2x > 1 jest przedział
f) Wykres funkcji y = 2 x znajduje się pod wykresem funkcji y = 4 w x<2 - это хорошо читается по рис. 203. Значит, решением неравенства 2х <4служит промежуток
Zapewne zauważyłeś, że podstawą wszystkich wniosków, jakie wyciągnięto przy rozwiązywaniu przykładu 1, była własność monotoniczności (wzrostu) funkcji y = 2 x. Podobne rozumowanie pozwala zweryfikować zasadność dwóch kolejnych twierdzeń. 
![]() , ale zbudujemy je nie w starym, ale w nowym układzie współrzędnych (punkty te zaznaczono na ryc. 207). Następnie z punktów skonstruujemy wykładnik - będzie to wymagany wykres (patrz ryc. 207).
, ale zbudujemy je nie w starym, ale w nowym układzie współrzędnych (punkty te zaznaczono na ryc. 207). Następnie z punktów skonstruujemy wykładnik - będzie to wymagany wykres (patrz ryc. 207).
Aby znaleźć największą i najmniejszą wartość danej funkcji na odcinku [-2, 2], wykorzystujemy fakt, że dana funkcja jest rosnąca i dlatego przyjmuje odpowiednio jej najmniejszą i największą wartość w punkcie lewy i prawy koniec segmentu.
Więc:![]()
Odpowiedź: a)x = 1; b)x>1; c)x<1.
![]() Udowodnij to
Udowodnij to ![]()
Rozwiązanie. Zgodnie z warunkiem, który mamy.



 największa wartość funkcji w segmencie
największa wartość funkcji w segmencie najmniejsza wartość funkcji w segmencie
najmniejsza wartość funkcji w segmencie