Una de las figuras tridimensionales más simples es la pirámide triangular, ya que consta del menor número de caras a partir de las cuales se puede formar una figura en el espacio. En este artículo veremos fórmulas que se pueden usar para encontrar el volumen de una pirámide triangular regular.
pirámide triangular
Según la definición general, una pirámide es un polígono, todos cuyos vértices están conectados a un punto que no se encuentra en el plano de este polígono. Si este último es un triángulo, entonces toda la figura se llama pirámide triangular.
La pirámide en cuestión consta de una base (triángulo) y tres caras laterales (triángulos). El punto en el que se conectan las tres caras laterales se llama vértice de la figura. La perpendicular desde este vértice hasta la base es la altura de la pirámide. Si el punto de intersección de la perpendicular con la base coincide con el punto de intersección de las medianas del triángulo en la base, entonces hablamos de una pirámide regular. De lo contrario quedará inclinado.
Como ya hemos dicho, la base de una pirámide triangular puede ser un tipo general de triángulo. Sin embargo, si es equilátero y la pirámide en sí es recta, entonces se habla de una figura tridimensional regular.
Cualquier pirámide triangular tiene 4 caras, 6 aristas y 4 vértices. Si las longitudes de todas las aristas son iguales, entonces dicha figura se llama tetraedro.
tipo general
Antes de escribir una pirámide triangular regular, damos una expresión para esta cantidad física para una pirámide de tipo general. Esta expresión se parece a:
Aquí S o es el área de la base, h es la altura de la figura. Esta igualdad será válida para cualquier tipo de base de polígono piramidal, así como para un cono. Si en la base hay un triángulo con una longitud de lado a y una altura h o bajada sobre él, entonces la fórmula para el volumen se escribirá de la siguiente manera:
Fórmulas para el volumen de una pirámide triangular regular.
Una pirámide triangular regular tiene un triángulo equilátero en la base. Se sabe que la altura de este triángulo está relacionada con la longitud de su lado por la igualdad:
Sustituyendo esta expresión en la fórmula del volumen de una pirámide triangular escrita en el párrafo anterior, obtenemos:
V = 1/6*a*h o *h = √3/12*a 2 *h.
El volumen de una pirámide regular de base triangular es función de la longitud del lado de la base y de la altura de la figura.
Dado que cualquier polígono regular puede inscribirse en un círculo, cuyo radio determinará de forma única la longitud del lado del polígono, entonces esta fórmula se puede escribir en términos del radio correspondiente r:
Esta fórmula se puede obtener fácilmente a partir de la anterior, si tenemos en cuenta que el radio r del círculo circunscrito que pasa por la longitud del lado a del triángulo está determinado por la expresión:
Problema de determinar el volumen de un tetraedro.
Mostraremos cómo utilizar las fórmulas anteriores al resolver problemas de geometría específicos.
Se sabe que un tetraedro tiene una longitud de arista de 7 cm. Encuentre el volumen de una pirámide-tetraedro triangular regular.
Recuerde que un tetraedro es regular en el que todas las bases son iguales entre sí. Para utilizar la fórmula del volumen triangular, necesitas calcular dos cantidades:
- longitud del lado del triángulo;
- altura de la figura.
La primera cantidad se conoce a partir del planteamiento del problema:
Para determinar la altura, considere la cifra que se muestra en la figura.

El triángulo marcado ABC es un triángulo rectángulo, donde el ángulo ABC mide 90°. El lado AC es la hipotenusa y su longitud es a. Usando un razonamiento geométrico simple, se puede demostrar que el lado BC tiene la longitud:
Tenga en cuenta que la longitud BC es el radio del círculo circunscrito alrededor del triángulo.
h = AB = √(AC 2 - BC 2) = √(a 2 - a 2 /3) = a*√(2/3).
Ahora puedes sustituir h y a en la fórmula correspondiente para el volumen:
V = √3/12*a 2 *a*√(2/3) = √2/12*a 3 .
Así, hemos obtenido la fórmula para el volumen de un tetraedro. Se puede ver que el volumen depende únicamente de la longitud del borde. Si sustituimos el valor de las condiciones del problema en la expresión, obtenemos la respuesta:
V = √2/12*7 3 ≈ 40,42 cm 3.
Si comparamos este valor con el volumen de un cubo que tiene la misma arista, encontramos que el volumen del tetraedro es 8,5 veces menor. Esto indica que el tetraedro es una figura compacta que se presenta en algunas sustancias naturales. Por ejemplo, la molécula de metano tiene forma tetraédrica y cada átomo de carbono del diamante está conectado a otros cuatro átomos para formar un tetraedro.

Problema de la pirámide homotética
Resolvamos un problema geométrico interesante. Supongamos que hay una pirámide regular triangular con un cierto volumen V 1. ¿Cuántas veces se debe reducir el tamaño de esta figura para obtener una pirámide homotética con un volumen tres veces menor que el original?

Comencemos a resolver el problema escribiendo la fórmula de la pirámide regular original:
V 1 = √3/12*a 1 2 *h 1 .
Deje que el volumen de la figura requerido por las condiciones del problema se obtenga multiplicando sus parámetros por el coeficiente k. Tenemos:
V 2 = √3/12*k 2 *a 1 2 *k*h 1 = k 3 *V 1 .
Dado que la relación de los volúmenes de las figuras se conoce por la condición, obtenemos el valor del coeficiente k:
k = ∛(V 2 /V 1) = ∛(1/3) ≈ 0,693.
Tenga en cuenta que obtendríamos un valor similar para el coeficiente k para una pirámide de cualquier tipo, y no sólo para una triangular normal.
Metas y objetivos de la lección:
- derivar fórmulas para el volumen de una pirámide usando la fórmula básica para el volumen de cuerpos y el volumen de una pirámide truncada.
- Sistematizar conocimientos teóricos sobre el tema de encontrar el volumen de una pirámide.
- Desarrollar la habilidad de encontrar el volumen de una pirámide cuyo vértice se proyecta hacia el centro de un círculo inscrito o circunscrito cerca de la base.
- Desarrollar habilidades para resolver problemas estándar usando fórmulas para los volúmenes de una pirámide y una pirámide truncada.
Progreso de la lección
I.Explicaciónmaterial nuevo.
La demostración del teorema se realiza mediante un proyector multimedia.
Demostremos el teorema: el volumen de la pirámide esun tercio, el producto del área de la base por la altura.

Prueba:
Primero demostramos el teorema de una pirámide triangular y luego de una arbitraria.
1. Considere una pirámide triangular OABC con volumen V, área base S y altura h. Dibujemos el eje oh (OM2- altura), considere la sección A 1 B 1 C 1 pirámide con un plano perpendicular al eje Oh y, por tanto, paralelo al plano de la base. Denotemos por incógnita punto de abscisa METRO 1
intersección de este plano con el eje x, y a través de S(incógnita)- área de la sección transversal. vamos a expresar S(incógnita) a través de S, h Y incógnita. Tenga en cuenta que ![]()
En efecto , por eso, .
Triángulos Rectángulos ![]() , también son similares (tienen un ángulo agudo común con el vértice ACERCA DE).
, también son similares (tienen un ángulo agudo común con el vértice ACERCA DE).

Apliquemos ahora la fórmula básica para calcular los volúmenes de cuerpos en a = 0, segundo =h obtenemos

2. Demostremos ahora el teorema de una pirámide arbitraria con altura h y área base S. Una pirámide de este tipo se puede dividir en pirámides triangulares con una altura total h. Expresemos el volumen de cada pirámide triangular usando la fórmula que hemos probado y sumemos estos volúmenes. Sacando el factor común de paréntesis, obtenemos entre paréntesis la suma de las bases de pirámides triangulares, es decir área S de las bases de la pirámide original.
Por tanto, el volumen de la pirámide original es. El teorema ha sido demostrado.
II. Resolver problemas utilizando dibujos ya hechos.

Tarea 1. (Fig.3)
Dado:abecedarioD- pirámide regular AB = 3; anuncio= . Encontrar: A) Sbásico; b) JSC; V) HACER GRAMO) V .
Tarea 2. (Fig.4)
Dado:abecedarioDF- pirámide regular .
Tarea 3. (Fig.5)
Dado:abecedarioDEKF- pirámide regular
Encontrar: A) Sbásico ; b) v.
Tarea4. (fig.. 6)
Encontrar: v.
Los problemas se prueban utilizando un proyector multimedia con un análisis detallado de una solución paso a paso.
Tarea 1. (Fig.3)
a) (la fórmula se utiliza para calcular el área de un triángulo regular)
AB = = 3, tenemos ![]()
b) ![]() (fórmula para el radio de un círculo circunscrito usando el lado de un triángulo equilátero)
(fórmula para el radio de un círculo circunscrito usando el lado de un triángulo equilátero) ![]() .
.

Tarea 2. (Fig.4)
1) Consideremos, pues,
– isósceles, OS = FO = 2.

Tarea 3. (Fig.5)

Tarea 4. (Fig.6)

III. Comprobar el resultado de la fórmula para calcular el volumen de una pirámide truncada (el mensaje del alumno en la pizarra se realiza mediante un proyector multimedia)
Respuesta del estudiante:
El volumen de una pirámide truncada se considera como la diferencia entre los volúmenes de la pirámide completa y el que está cortado de ella por un plano paralelo a la base (Fig. 1).


Sustituyamos esta expresión por incógnita en la primera fórmula,

Trabajo en forma de test, con verificación a través de un proyector multimedia.
1. En un prisma inclinado, el borde lateral mide 7 cm, la sección perpendicular es un triángulo rectángulo con catetos: 4 cm y 3 cm. Calcula el volumen del prisma.
a) 10 cm 3, b) 42 cm 3, c) 60 cm 3, d) 30 cm 3.
2. En una pirámide hexagonal regular, el lado de su base mide 2 cm. El volumen de la pirámide es 6 cm 3. ¿Cuál es la altura?

3. El volumen de la pirámide es de 56 cm 3, el área de la base es de 14 cm 2. ¿Cuál es la altura?
a) 14 cm, b) 12 cm, c) 16 cm.
4. En una pirámide triangular regular, la altura es de 5 cm y los lados de la base miden 3 cm. ¿Cuál es el volumen de la pirámide?

5. En una pirámide cuadrangular regular, la altura es de 9 cm. El lado de la base mide 4 cm.
a) 50 cm 3, b) 48 cm 3, c) 16 cm 3.
6. El volumen de una pirámide cuadrangular regular es 27 cm 3, altura 9 cm Encuentra el lado de la base.
a) 12 cm, b) 9 cm, c) 3 cm.
7. El volumen de una pirámide truncada es de 210 cm 3, el área de la base inferior es de 36 cm 2 y la superior es de 9 cm 2. Encuentra la altura de la pirámide.
a) 1 cm, b) 15 cm, c) 10 cm.
8. Un prisma del mismo tamaño y una pirámide cuadrangular regular tienen alturas iguales. ¿Cuál es el lado de la base de la pirámide si el área de la base del prisma es S?

Tabla de respuestas.
| Tarea | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Respuesta | b | A | b | A | b | V | V | V |
Tarea: 1. Resolver los problemas No. 695v, No. 697, No. 690
2. Considere las tareas básicas
Tarea 1.
Demuestre que si los bordes laterales de la pirámide son iguales (o forman ángulos iguales con el plano de la base), entonces la cima de la pirámide se proyecta hacia el centro del círculo circunscrito alrededor de la base.

Demuestre que si los ángulos diédricos en la base de la pirámide son iguales (o iguales a las alturas de las caras laterales dibujadas desde el vértice de la pirámide), entonces el vértice de la pirámide se proyecta hacia el centro del círculo inscrito en el base de la pirámide.

Aquí veremos ejemplos relacionados con el concepto de volumen. Para resolver este tipo de problemas, debes conocer la fórmula para calcular el volumen de una pirámide:

S
h – altura de la pirámide
La base puede ser cualquier polígono. Pero en la mayoría de los problemas del Examen Estatal Unificado, la condición suele referirse a pirámides regulares. Déjame recordarte una de sus propiedades:
La cima de una pirámide regular se proyecta hacia el centro de su base.
Mire la proyección de las pirámides regulares triangulares, cuadrangulares y hexagonales (VISTA SUPERIOR):

Puedes hacerlo en el blog, donde se discutieron los problemas relacionados con encontrar el volumen de una pirámide.Consideremos las tareas:
27087. Calcula el volumen de una pirámide triangular regular cuyos lados de base son iguales a 1 y cuya altura es igual a la raíz de tres.


S– área de la base de la pirámide
h– altura de la pirámide
Encontremos el área de la base de la pirámide, este es un triángulo regular. Usemos la fórmula: el área de un triángulo es igual a la mitad del producto de los lados adyacentes por el seno del ángulo entre ellos, lo que significa:


Respuesta: 0,25
27088. Calcula la altura de una pirámide triangular regular cuyos lados de la base son iguales a 2 y cuyo volumen es igual a la raíz de tres.

Conceptos como la altura de una pirámide y las características de su base están relacionados mediante la fórmula del volumen:

S– área de la base de la pirámide
h– altura de la pirámide
Conocemos el volumen en sí, podemos encontrar el área de la base, ya que conocemos los lados del triángulo, que es la base. Conociendo los valores indicados, podemos encontrar fácilmente la altura.
Para encontrar el área de la base, usamos la fórmula: el área de un triángulo es igual a la mitad del producto de los lados adyacentes y el seno del ángulo entre ellos, lo que significa:

Así, sustituyendo estos valores en la fórmula del volumen, podemos calcular la altura de la pirámide:

La altura es tres.
Respuesta: 3
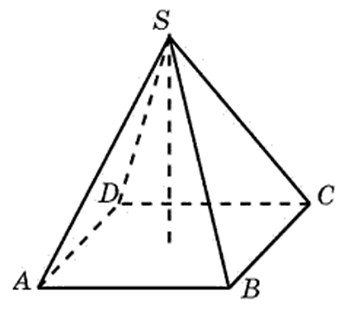
27109. En una pirámide cuadrangular regular, la altura es 6 y el borde lateral es 10. Encuentra su volumen.
El volumen de la pirámide se calcula mediante la fórmula:

S– área de la base de la pirámide
h– altura de la pirámide
Sabemos la altura. Necesitas encontrar el área de la base. Permítanme recordarles que la cima de una pirámide regular se proyecta hacia el centro de su base. La base de una pirámide cuadrangular regular es un cuadrado. Podemos encontrar su diagonal. Considere un triángulo rectángulo (resaltado en azul):

El segmento que conecta el centro del cuadrado con el punto B es un cateto que es igual a la mitad de la diagonal del cuadrado. Podemos calcular este cateto usando el teorema de Pitágoras:
Esto significa BD = 16. Calculemos el área del cuadrado usando la fórmula para el área de un cuadrilátero:

Por eso:
Por tanto, el volumen de la pirámide es:

Respuesta: 256
27178. En una pirámide cuadrangular regular, la altura es 12 y el volumen es 200. Encuentra el borde lateral de esta pirámide.

Se conoce la altura de la pirámide y su volumen, lo que significa que podemos encontrar el área del cuadrado, que es la base. Conociendo el área de un cuadrado podemos encontrar su diagonal. A continuación, considerando un triángulo rectángulo usando el teorema de Pitágoras, calculamos la arista lateral:

Encontremos el área del cuadrado (base de la pirámide):

Calculemos la diagonal del cuadrado. Como su área es 50, el lado será igual a la raíz de cincuenta y según el teorema de Pitágoras:
El punto O divide la diagonal BD por la mitad, lo que significa que el cateto del triángulo rectángulo OB = 5.
Así, podemos calcular a qué es igual el borde lateral de la pirámide:
Respuesta: 13
245353. Encuentra el volumen de la pirámide que se muestra en la figura. Su base es un polígono cuyos lados adyacentes son perpendiculares y uno de los bordes laterales es perpendicular al plano de la base e igual a 3.

Como se ha dicho muchas veces, el volumen de la pirámide se calcula mediante la fórmula:

S– área de la base de la pirámide
h– altura de la pirámide
El borde lateral perpendicular a la base es igual a tres, lo que significa que la altura de la pirámide es tres. La base de la pirámide es un polígono cuya área es igual a:
De este modo:

Respuesta: 27
27086. La base de la pirámide es un rectángulo con lados 3 y 4. Su volumen es 16. Calcula la altura de esta pirámide.
Eso es todo. ¡Buena suerte para ti!
Atentamente, Alexander Krutitskikh.
P.D: Le agradecería que me hablara del sitio en las redes sociales.
La principal característica de cualquier figura geométrica en el espacio es su volumen. En este artículo veremos qué es una pirámide con un triángulo en la base y también mostraremos cómo encontrar el volumen de una pirámide triangular: regular, completa y truncada.
¿Qué es esto? ¿Una pirámide triangular?
Todo el mundo ha oído hablar de las pirámides del antiguo Egipto, pero son cuadrangulares regulares, no triangulares. Expliquemos cómo conseguir una pirámide triangular.
Tomemos un triángulo arbitrario y conectemos todos sus vértices con algún punto ubicado fuera del plano de este triángulo. La figura resultante se llamará pirámide triangular. Se muestra en la siguiente figura.
Como puedes ver, la figura en cuestión está formada por cuatro triángulos, que en el caso general son diferentes. Cada triángulo son los lados de la pirámide o su cara. Esta pirámide a menudo se llama tetraedro, es decir, figura tridimensional tetraédrica.
Además de los lados, la pirámide también tiene aristas (hay 6) y vértices (de 4).
con base triangular
Una figura que se obtiene utilizando un triángulo arbitrario y un punto en el espacio será una pirámide inclinada irregular en el caso general. Ahora imagine que el triángulo original tiene lados idénticos y un punto en el espacio está ubicado exactamente encima de su centro geométrico a una distancia h del plano del triángulo. La pirámide construida con estos datos iniciales será correcta.
Evidentemente, el número de aristas, lados y vértices de una pirámide triangular regular será el mismo que el de una pirámide construida a partir de un triángulo arbitrario.
Sin embargo, la figura correcta tiene algunas características distintivas:
- su altura extraída desde el vértice interceptará exactamente la base en el centro geométrico (el punto de intersección de las medianas);
- la superficie lateral de dicha pirámide está formada por tres triángulos idénticos, que son isósceles o equiláteros.
Una pirámide triangular regular no es sólo un objeto geométrico puramente teórico. Algunas estructuras en la naturaleza tienen su forma, por ejemplo la red cristalina del diamante, donde un átomo de carbono está conectado a cuatro átomos iguales mediante enlaces covalentes, o una molécula de metano, donde los vértices de la pirámide están formados por átomos de hidrógeno.

pirámide triangular
Puedes determinar el volumen de absolutamente cualquier pirámide con un n-gón arbitrario en la base usando la siguiente expresión:
Aquí el símbolo S o denota el área de la base, h es la altura de la figura dibujada hasta la base marcada desde la cima de la pirámide.
Dado que el área de un triángulo arbitrario es igual a la mitad del producto de la longitud de su lado a y la apotema h a caída en este lado, la fórmula para el volumen de una pirámide triangular se puede escribir de la siguiente forma:
V = 1/6 × a × h a × h
Para el tipo general, determinar la altura no es una tarea fácil. Para resolverlo, la forma más sencilla es utilizar la fórmula de la distancia entre un punto (vértice) y un plano (base triangular), representada por una ecuación general.

Para el correcto, tiene una apariencia específica. El área de la base (de un triángulo equilátero) es igual a:
Sustituyéndolo en la expresión general de V, obtenemos:
V = √3/12 × a 2 × h
Un caso especial es la situación en la que todos los lados de un tetraedro resultan ser triángulos equiláteros idénticos. En este caso, su volumen sólo puede determinarse basándose en el conocimiento del parámetro de su borde a. La expresión correspondiente se ve así:
Pirámide truncada
Si la parte superior que contiene el vértice se corta de una pirámide triangular regular, se obtiene una figura truncada. A diferencia del original, estará formado por dos bases triangulares equiláteras y tres trapecios isósceles.
La foto de abajo muestra cómo se ve una pirámide triangular truncada regular hecha de papel.

Para determinar el volumen de una pirámide triangular truncada es necesario conocer sus tres características lineales: cada uno de los lados de las bases y la altura de la figura, igual a la distancia entre las bases superior e inferior. La fórmula correspondiente para el volumen se escribe de la siguiente manera:
V = √3/12 × h × (A 2 + a 2 + A × a)
Aquí h es la altura de la figura, A y a son las longitudes de los lados de los triángulos equiláteros grande (inferior) y pequeño (superior), respectivamente.
solución del problema
Para que la información del artículo sea más clara para el lector, mostraremos con un ejemplo claro cómo utilizar algunas de las fórmulas escritas.
Sea el volumen de la pirámide triangular 15 cm 3 . Se sabe que la cifra es correcta. Es necesario encontrar la apotema a b del borde lateral si se sabe que la altura de la pirámide es de 4 cm.
Como se conocen el volumen y la altura de la figura, puedes utilizar la fórmula adecuada para calcular la longitud del lado de su base. Tenemos:
V = √3/12 × a 2 × h =>
a = 12 × V / (√3 × h) = 12 × 15 / (√3 × 4) = 25,98 cm
a b = √(h 2 + a 2/12) = √(16 + 25,98 2/12) = 8,5 cm
La longitud calculada de la apotema de la figura resultó ser mayor que su altura, lo cual es válido para cualquier tipo de pirámide.
Una de las figuras tridimensionales más simples es la pirámide triangular, ya que consta del menor número de caras a partir de las cuales se puede formar una figura en el espacio. En este artículo veremos fórmulas que se pueden usar para encontrar el volumen de una pirámide triangular regular.
pirámide triangular
Según la definición general, una pirámide es un polígono, todos cuyos vértices están conectados a un punto que no se encuentra en el plano de este polígono. Si este último es un triángulo, entonces toda la figura se llama pirámide triangular.
La pirámide en cuestión consta de una base (triángulo) y tres caras laterales (triángulos). El punto en el que se conectan las tres caras laterales se llama vértice de la figura. La perpendicular desde este vértice hasta la base es la altura de la pirámide. Si el punto de intersección de la perpendicular con la base coincide con el punto de intersección de las medianas del triángulo en la base, entonces hablamos de una pirámide regular. De lo contrario quedará inclinado.
Como ya hemos dicho, la base de una pirámide triangular puede ser un tipo general de triángulo. Sin embargo, si es equilátero y la pirámide en sí es recta, entonces se habla de una figura tridimensional regular.
Cualquier pirámide triangular tiene 4 caras, 6 aristas y 4 vértices. Si las longitudes de todas las aristas son iguales, entonces dicha figura se llama tetraedro.
Volumen de una pirámide triangular general.
Antes de escribir la fórmula para el volumen de una pirámide triangular regular, damos una expresión para esta cantidad física para una pirámide de tipo general. Esta expresión se parece a:
Sobre el tema: Inga Budkevich: biografía y filmografía de la actriz.
Aquí S o es el área de la base, h es la altura de la figura. Esta igualdad será válida para cualquier tipo de base de polígono piramidal, así como para un cono. Si en la base hay un triángulo con una longitud de lado a y una altura h o bajada sobre él, entonces la fórmula para el volumen se escribirá de la siguiente manera:
V = 1/6*a*h o *h.
Fórmulas para el volumen de una pirámide triangular regular.
Una pirámide triangular regular tiene un triángulo equilátero en la base. Se sabe que la altura de este triángulo está relacionada con la longitud de su lado por la igualdad:
Sustituyendo esta expresión en la fórmula del volumen de una pirámide triangular escrita en el párrafo anterior, obtenemos:
V = 1/6*a*h o *h = √3/12*a 2 *h.
El volumen de una pirámide regular de base triangular es función de la longitud del lado de la base y de la altura de la figura.
Dado que cualquier polígono regular puede inscribirse en un círculo, cuyo radio determinará de forma única la longitud del lado del polígono, entonces esta fórmula se puede escribir en términos del radio correspondiente r:
V = √3/4*h*r 2 .
Esta fórmula se puede obtener fácilmente a partir de la anterior, si tenemos en cuenta que el radio r del círculo circunscrito que pasa por la longitud del lado a del triángulo está determinado por la expresión:
Problema de determinar el volumen de un tetraedro.
Mostraremos cómo utilizar las fórmulas anteriores al resolver problemas de geometría específicos.
Se sabe que un tetraedro tiene una longitud de arista de 7 cm. Encuentre el volumen de una pirámide-tetraedro triangular regular.
Recordemos que un tetraedro es una pirámide triangular regular en la que todas las bases son iguales entre sí. Para usar la fórmula para el volumen de una pirámide triangular regular, necesitas calcular dos cantidades:
Sobre el tema: Estación principal de Praga: dirección, descripción. Viajar a Praga en tren
- longitud del lado del triángulo;
- altura de la figura.
La primera cantidad se conoce a partir del planteamiento del problema:
Para determinar la altura, considere la cifra que se muestra en la figura.

El triángulo marcado ABC es un triángulo rectángulo, donde el ángulo ABC mide 90°. El lado AC es la hipotenusa y su longitud es a. Usando un razonamiento geométrico simple, se puede demostrar que el lado BC tiene la longitud:
Tenga en cuenta que la longitud BC es el radio del círculo circunscrito alrededor del triángulo.
h = AB = √(AC 2 - BC 2) = √(a 2 - a 2 /3) = a*√(2/3).
Ahora puedes sustituir h y a en la fórmula correspondiente para el volumen:
V = √3/12*a 2 *a*√(2/3) = √2/12*a 3 .
Así, hemos obtenido la fórmula para el volumen de un tetraedro. Se puede ver que el volumen depende únicamente de la longitud del borde. Si sustituimos el valor de las condiciones del problema en la expresión, obtenemos la respuesta:
V = √2/12*7 3 ≈ 40,42 cm 3.
Si comparamos este valor con el volumen de un cubo que tiene la misma arista, encontramos que el volumen del tetraedro es 8,5 veces menor. Esto indica que el tetraedro es una figura compacta que se presenta en algunas sustancias naturales. Por ejemplo, la molécula de metano tiene forma tetraédrica y cada átomo de carbono del diamante está conectado a otros cuatro átomos para formar un tetraedro.

Problema de la pirámide homotética
