fórmula de elección

1. Introducción

2. Fórmula de Peak. Anexo I.

Prueba II.

Prueba sh.

3. Objetivos.

4. Fórmula para el área de un polígono utilizando las coordenadas de los vértices.

5. Tareas.

6. Literatura

La fórmula de Peak.

1. Introducción.

Extraemos sabiduría de la historia,

en poesía - ingenio,

en matemáticas - perspicacia.

F. tocino

La trama se desarrollará en una hoja de papel normal y corriente.

Las líneas que corren a lo largo de los lados de las celdas forman una cuadrícula, y la parte superior de las celdas son los nodos de esta cuadrícula. Dibujemos un polígono en la hoja con vértices en los nodos y encontremos su área.

Puedes buscarlo de diferentes formas. Por ejemplo, puedes cortar un polígono en formas bastante simples, encontrar sus áreas y sumarlas.

Pero aquí nos esperan muchos problemas. La figura se divide fácilmente en rectángulos, trapecios y triángulos, y su área se calcula sin esfuerzo.

Aunque el polígono parece bastante simple, calcular su área requiere mucho trabajo. ¿Qué pasaría si el polígono pareciera más elegante? Resulta que las áreas de los polígonos cuyos vértices se encuentran en los nodos de la cuadrícula se pueden calcular de manera mucho más sencilla: existe una fórmula que relaciona su área con el número de nodos que se encuentran dentro y en el borde del polígono. Esta maravillosa y sencilla fórmula se llama fórmula Pick.

2. Fórmula de Peak.

Los vértices de un polígono (no necesariamente convexos) están ubicados en los nodos de una red de números enteros. En su interior se encuentran los nodos B de la red y en el límite hay nodos G. Demostremos que su área es igual a B + – 1 (Elegir fórmula).

Anexo I.

Consideremos un polígono cuyos vértices están ubicados en los nodos de una red entera, es decir, tienen coordenadas enteras.

Dividimos el polígono en triángulos con vértices en los nodos de la red, que no contienen nodos ni en el interior ni en los lados.

Denotemos:

norte– número de lados del polígono,

metro– el número de triángulos con vértices en nodos de red que no contienen nodos ni en el interior ni en los lados,

B – número de nodos dentro del polígono,

Г – número de nodos en los lados, incluidos los vértices.

Las áreas de todos estos triángulos son iguales e iguales.

Por tanto, el área del polígono es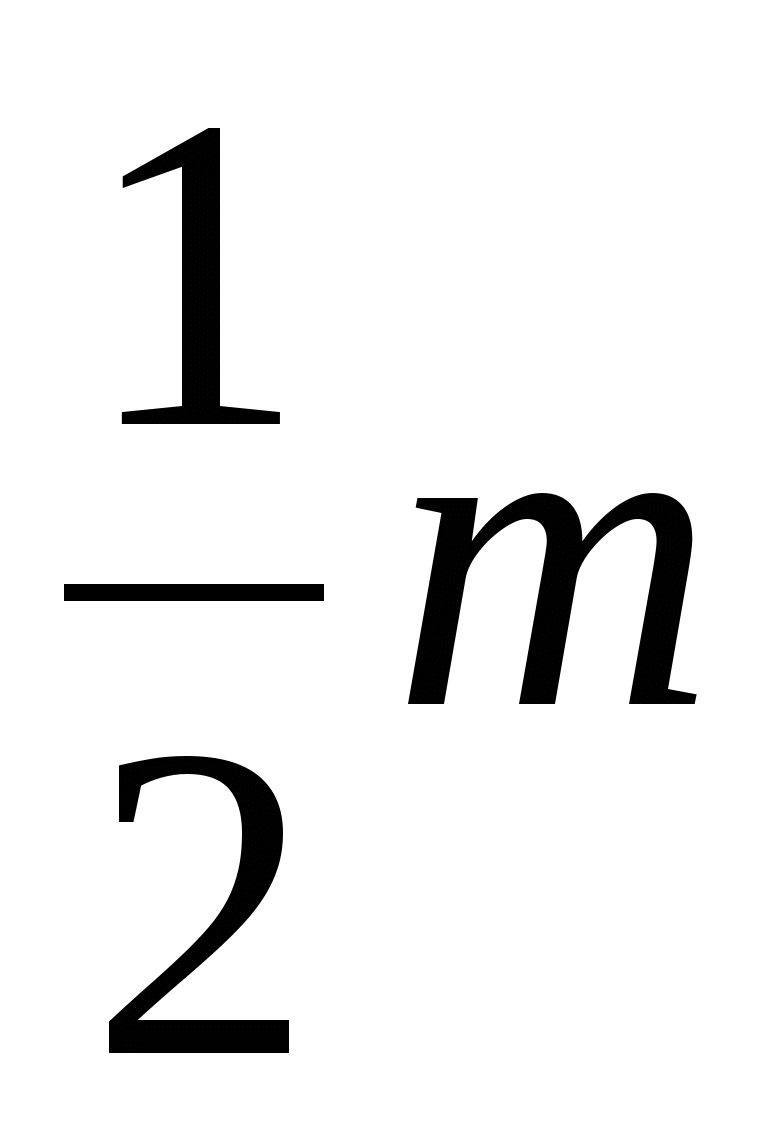
.

180 0 metro .

Ahora encontremos esta cantidad de otra manera.

La suma de los ángulos con vértice en cualquier nodo interno es 360 0.

Entonces la suma de los ángulos con vértices en todos los nodos internos es igual a 360 0 V.

La suma total de los ángulos de los nodos en los lados, pero no en los vértices, es 180 0 (G - norte).

La suma de los ángulos en los vértices del polígono es 180 0 ( norte – 2) .

La suma total de los ángulos de todos los triángulos es 360 0 V + 180 0 (G – norte) + 180 0 (norte – 2).

entonces 180 0 metro= 360 0 V + 180 0 (G – norte) + 180 0 (norte – 2),

180 0 metro= 360 0 V + 180 0 G – 180 0 norte + 180 0 norte– 180 0 2,

180 0 metro= 360 0 V + 180 0 G – 360 0,

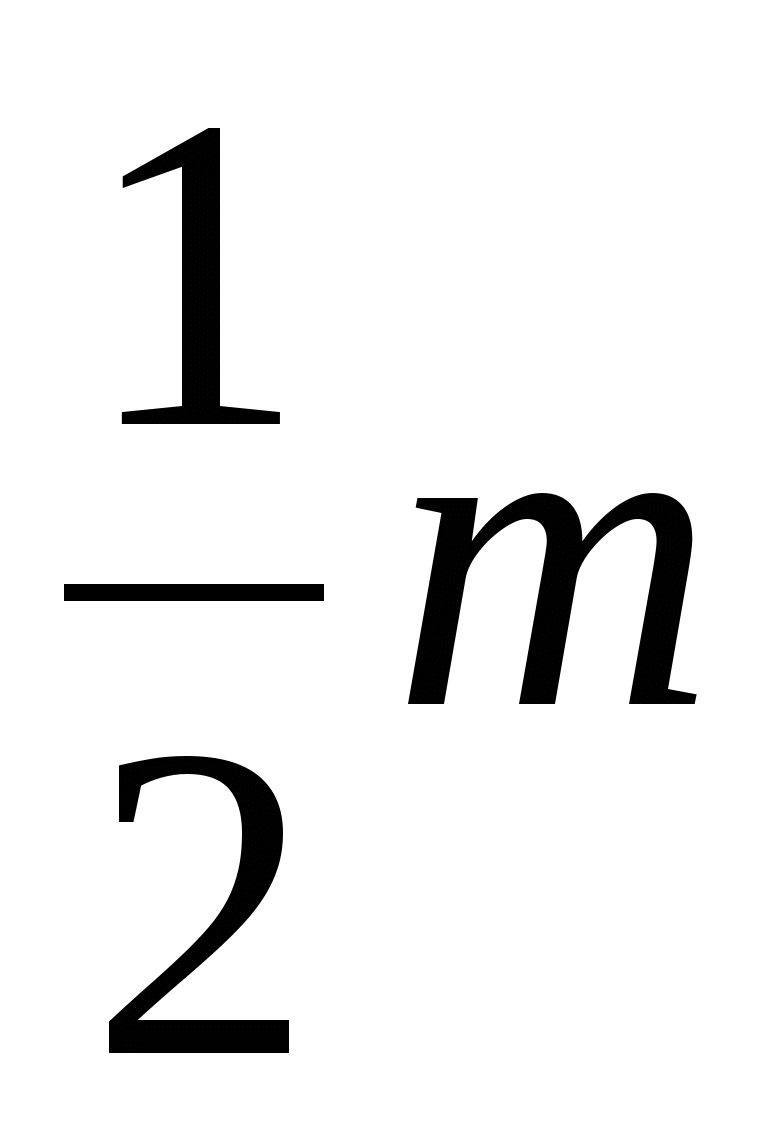= B + – 1 ,

de donde obtenemos la expresión para el área S del polígono:

S= B + – 1 ,

conocida como fórmula de Pick.

En la figura: B = 24, D = 9, por lo tanto,S = 24 + – 1 = 27,5.

Encontremos el área del primer polígono usando la fórmula de Peak:

B = 28 (puntos verdes);

G = 20 (puntos azules).

Obtenemos, S =
= 37 unidades cuadradas

Prueba II.

A cada polígono M con vértices en los nodos de una red entera le asignamos un número f (M) =
, donde la suma se realiza sobre todos los nodos de la red que pertenecen a M, y el ángulo se define de la siguiente manera: =
para el punto interior del polígono, =
para un punto límite distinto de un vértice, y – ángulo del vértice, si este nodo es un vértice. Es fácil ver que f(M) =
+
= B + – 1. Queda por comprobar que el número f (M) es igual al área del polígono M.

Sea el polígono M cortado en polígonos M 1 y M 2 con vértices en los nodos de la red. Entonces f (M) = f (M 1) + f (M 2), ya que para cada nodo se suman los ángulos. Por lo tanto, si la fórmula de Pick es verdadera para dos de los polígonos M, M 1 y M 2, entonces también lo es para el tercero.

Si M es un rectángulo con lados pag Y q, dirigido a lo largo de las líneas de la red, entonces

f (M) = (p – 1)(q – 1) +
= pq.

En este caso, la fórmula de Peak es válida. Cortando un rectángulo M con una diagonal en triángulos M 1 y M 2 y usando el hecho de que f (M) = f (M 1) + f (M 2) y f (M 1) = f (M 2), se Es fácil demostrar la validez de la fórmula de Pick para cualquier triángulo rectángulo con catetos dirigidos a lo largo de las líneas de la red. Al cortar varios de estos triángulos de un rectángulo, puedes obtener cualquier triángulo.

Para completar la prueba de la fórmula de Pick, queda señalar que cualquier polígono se puede cortar en triángulos mediante diagonales disjuntas.

Prueba sh.

La relación entre el área de una figura y el número de nodos incluidos en esta figura es especialmente visible en el caso de un rectángulo.

Dejar ABCD- un rectángulo con vértices en los nodos y lados a lo largo de las líneas de la cuadrícula.

Denotemos por EN el número de nodos que se encuentran dentro del rectángulo y a través de GRAMO- el número de nodos en su frontera. Movamos la cuadrícula media celda hacia la derecha y media celda hacia abajo.

Entonces el territorio del rectángulo se puede "distribuir" entre los nodos de la siguiente manera: cada uno de EN Los nodos "controlan" una celda completa de la cuadrícula desplazada, cada uno de GRAMO– 4 nodos fronterizos que no son esquinas son media celda y cada uno de los puntos de las esquinas es un cuarto de celda. Por tanto, el área del rectángulo S es igual a

Entonces, para rectángulos con vértices en nodos y lados a lo largo de las líneas de la cuadrícula, hemos establecido la fórmula

Demostremos que esta fórmula es cierta no solo para rectángulos, sino también para polígonos arbitrarios con vértices en los nodos de la cuadrícula.

Denotemos por S metro área del polígonoMETRO con vértices en los nodos, y a través dePAG metro - tamaño
, DóndeEN metro – número de nodos dentroMETRO, A GRAMO metro - número de nodos en la frontera. Entonces la fórmula de Peak se puede escribir como
.

Dividiremos la prueba de la fórmula en varios pasos.

Paso 1.

Si el polígonoMETRO con vértices en los nodos de malla cortados en 2 polígonosMETRO 1 Y METRO 2 , también teniendo vértices solo en los nodos de la cuadrícula, entonces
. Deja que el polígonoMETRO cortar en polígonosMETRO 1 Y METRO 2 con vértices en nodos por un segmento AB. Todos los nodos excepto los que caen en el segmento.AB, hacer contribuciones iguales a los lados izquierdo y derecho de la fórmula. Consideremos los nodos que se encuentran en el segmento AB.

Si dicho nodo se encuentra entre A y B (por ejemplo, C), entonces para un polígonoMETRO es interno y para polígonosMETRO 1 Y METRO 2 – límite. Por ello su contribución aPAG metro es igual a 1, y en cada una de las expresiones
Y
– 0,5 cada uno, es decir, las contribuciones de dicho nodo aPAG metro Y
son iguales.

Consideremos los nodos A y B. Son nodos límite para ambos. METRO, y para METRO 1 , METRO 2 .

Por tanto, la contribución de cada uno de estos nodos aPAG metro igual a 0,5 a pulg
- unidad. Esto significa que la contribución total de los nodos A y B aPAG metro es igual a 1, que es 1 menos que su contribución a
. Pero
, A .

De la “contribución” total de todos los nodos PAG metro Se resta 1 y de
Se resta 2 y esto compensa la diferencia en las contribuciones de los nodos A y B.

Entonces,
.

Paso 2.

Si el polígono METRO con vértices en los nodos de la malla cortados en dos polígonos METRO 1 Y METRO 2 (también con vértices en los nodos) y la fórmula es correcta para algunos dos de los polígonos MM 1 , m 2 , entonces también es válido para el tercer polígono.

Sea, por ejemplo, cierto paraMETRO 1 Y METRO 2 , eso es
. Luego (por el primer paso), pero (por primer paso) la última expresión es igual aPAG metro , y la igualdad
y existe la fórmula Peak.

Paso 3.

Probemos la fórmula de Peak para un triángulo rectángulo con vértices en los nodos de la cuadrícula y catetos sobre líneas de la cuadrícula.

Triángulo abecedario construirlo en un rectángulo ABCD .

Para rectángulos, la fórmula de Pick es correcta: S ABCD =P ABCD . Según el primer paso PAG ABCD =P abecedario +P ACD , PAG abecedario =P ACD , Entonces PAG ABCD = 2P abecedario . Pero S ABCD = 2 S abecedario . Es por eso S abecedario =P abecedario .

Paso 4.

La fórmula de Pick es válida para un triángulo arbitrario con vértices en los nodos de la cuadrícula.

Habiendo examinado la figura, es fácil de entender: cualquier triángulo de este tipo se puede obtener "cortando" de un determinado rectángulo con lados a lo largo de las líneas de la cuadrícula, varios rectángulos y triángulos rectángulos con catetos a lo largo de las líneas de la cuadrícula. Y dado que la fórmula de Peak es válida para rectángulos y triángulos rectángulos, entonces (recuerde el paso 2) también es válida para el triángulo original.

Hemos demostrado que si un polígono se puede cortar en triángulos con vértices en los nodos de la cuadrícula, entonces la fórmula de Peak es válida para él.

3. Objetivos.

Encuentra el área de las figuras:

1
.

B=9

GRAMO = 4

B=9

G = 5

Un polígono sin autointersecciones se llama celosía si todos sus vértices están ubicados en puntos con coordenadas enteras (en el sistema de coordenadas cartesiano).

teorema de pick

Fórmula

Se nos dará un polígono de celosía con un área distinta de cero.

Denotemos su área por ; el número de puntos con coordenadas enteras que se encuentran estrictamente dentro del polígono; el número de puntos con coordenadas enteras que se encuentran en los lados del polígono.

Entonces la relación llamada fórmula de elección:

En particular, si se conocen los valores de I y B para un determinado polígono, entonces su área se puede calcular como , incluso sin conocer las coordenadas de sus vértices.

Esta relación fue descubierta y demostrada por el matemático austriaco Georg Alexander Pick en 1899.

Prueba

La demostración se realiza en varias etapas: desde las figuras más simples hasta polígonos arbitrarios:

Generalización a dimensiones superiores.

Desafortunadamente, esta sencilla y hermosa fórmula de Peake no se generaliza bien a dimensiones superiores.

Esto fue claramente demostrado por Reeve, quien propuso en 1957 considerar el tetraedro (ahora llamado tetraedro de reeve) con los siguientes vértices:

¿Dónde está cualquier número natural? Entonces este tetraedro, para cualquiera, no contiene un solo punto con coordenadas enteras en su interior, y en su límite solo hay cuatro puntos , , , y ningún otro. Así, el volumen y la superficie de este tetraedro pueden ser diferentes, mientras que el número de puntos dentro y en el borde no cambia; por tanto, la fórmula de Pick no permite generalizaciones ni siquiera al caso tridimensional.

Sin embargo, todavía existe alguna generalización similar a espacios de dimensiones superiores: esto polinomios de Ehrhart(Polinomio de Ehrhart), pero son muy complejos y dependen no sólo del número de puntos dentro y del borde de la figura.

Para estimar el área de un polígono en papel cuadriculado, basta con contar cuántas celdas cubre este polígono (tomamos el área de una celda como uno). Más precisamente, si S- el área del polígono, - el número de celdas que se encuentran completamente dentro del polígono, y - el número de celdas que tienen al menos un punto común con el interior del polígono.

A continuación consideraremos sólo aquellos polígonos cuyos vértices se encuentran en los nodos del papel cuadriculado, en aquellos donde se cruzan las líneas de la cuadrícula. Resulta que para tales polígonos se puede especificar la siguiente fórmula:

¿Dónde está el área? r- el número de nodos que se encuentran estrictamente dentro del polígono.

Esta fórmula se llama "fórmula Pick", en honor al matemático que la descubrió en 1899.

Triángulos simples

El área de cualquier triángulo dibujado en papel cuadriculado se puede calcular fácilmente representándola como la suma o diferencia de las áreas de triángulos rectángulos y rectángulos cuyos lados siguen las líneas de la cuadrícula que pasan por los vértices del triángulo dibujado. Habiendo hecho esto, por ejemplo, para los triángulos que se muestran en la Figura 1.34, puede asegurarse de que el área sea siempre igual al número "recibido", un número de la forma donde es un número entero.

Llamemos simple a un triángulo si no hay nodos de malla en su interior o en sus lados, a excepción de sus vértices. Todos los triángulos simples de la Fig. 1,34 tienen área. Veremos que esto no es casual.

Tarea. Tres saltamontes (tres puntos) en el momento inicial se sientan en los tres vértices de una celda y luego comienzan a "jugar al salto": cada uno puede saltar sobre uno de los otros dos, después de lo cual termina en un punto simétrico relativo por sí solo (Fig. 1.35, claramente, que después de cualquier número de tales saltos los saltamontes caerán en los nudos de papel cuadriculado). ¿En qué triples de puntos pueden acabar los saltamontes tras unos cuantos saltos?

Llamemos a un triángulo alcanzable si en sus vértices pueden aparecer simultáneamente tres saltamontes, que inicialmente estaban en tres vértices de una celda; Llamaremos salto a una transformación de triángulo, que consiste en que uno de los vértices va a un punto que es simétrico respecto a cualquiera de los otros dos vértices (estos dos vértices permanecen en su lugar).

Teorema 1. Las siguientes tres propiedades de triángulos con vértices en nodos de papel cuadriculado son equivalentes entre sí:

1) el triángulo tiene área,

2) el triángulo es simple,

3) el triángulo es alcanzable.

Conozcamos las siguientes propiedades de un triángulo simple, que conducen a la validez de este teorema.

1. El área del triángulo no cambia al saltar.

2. Cualquier triángulo alcanzable tiene área.

3. Si completas un triángulo simple abecedario al paralelogramo ABCD, entonces no habrá nodos (sin contar los vértices) ni dentro ni a los lados de este paralelogramo.

4. De un triángulo simple al saltar se obtiene un triángulo simple.

5. De un triángulo simple, uno de los ángulos es obtuso o recto (y este último caso sólo es posible para un triángulo cuyos tres vértices pertenecen a una celda; un triángulo tan simple con lados 1, 1 se llamará mínimo).

6. De cualquier triángulo simple no mínimo se puede obtener de un salto un triángulo cuyo lado mayor sea menor que el lado mayor del original.

7. Cualquier triángulo simple se puede convertir en uno mínimo mediante un número finito de saltos.

8. Cualquier triángulo simple es alcanzable.

9. Cualquier triángulo simple tiene área.

10. Cualquier triángulo se puede cortar en triángulos simples.

11. El área de cualquier triángulo es igual y cada vez que se corta en números primos, su número es igual. metro.

12. Cualquier triángulo de área es simple.

13. Para dos nodos cualesquiera A Y EN celosías, en un segmento entre el cual no hay otros nodos, hay un nodo CON tal que un triangulo abecedario- simple.

14. Nudo CON en la propiedad anterior siempre puedes elegir para que el ángulo dia será obtuso o recto.

15. Corte el plano cuadriculado en paralelogramos iguales de modo que todos los nodos sean vértices de paralelogramos. Entonces cada uno de los triángulos en que se corta uno de estos paralelogramos por su diagonal es simple.

16. (Reverso 15). Triángulo abecedario- simple si y sólo si todos los triángulos posibles se obtienen de abecedario traducciones paralelas transfiriendo el nodo A en diferentes nodos de red, no se superpongan entre sí.

17. Si la red, los nodos de papel cuadriculado, se divide en cuatro subredes con celdas (figura 1.36), entonces los vértices de un triángulo simple necesariamente caerán en tres subredes diferentes (las tres tienen designaciones diferentes).

Las dos propiedades siguientes proporcionan la respuesta al problema de los tres saltamontes.

18. Tres saltamontes pueden golpear simultáneamente aquellos y sólo aquellos tripletes de puntos que sirven como vértices de un triángulo simple y tienen el mismo signo que los vértices correspondientes del triángulo inicial.

19. Dos saltamontes pueden golpear simultáneamente aquellos y sólo aquellos pares de nodos de los signos correspondientes, en el segmento entre los cuales no hay otros nodos.

Triangulación de polígonos

Consideraremos un tipo particular de polígonos en papel cuadriculado, que corresponden a valores en la fórmula Pick. Pero de este caso particular se puede pasar directamente al más general, utilizando el teorema de cortar un polígono arbitrario en triángulos (ya no se necesita papel cuadriculado).

Sea un polígono y un conjunto finito en el plano. A puntos que se encuentran dentro del polígono y en su borde (y todos los vértices del polígono pertenecen al conjunto A).

Triangulación con vértices A se llama partición de un polígono dado en triángulos con vértices en el conjunto A tal que cada punto de A sirve como vértice de cada uno de esos triángulos de triangulación a los que pertenece este punto (es decir, puntos de A no caiga dentro ni a los lados de los triángulos, fig. 1.37).

Teorema 2. a) Cualquiera norte-un triángulo se puede cortar diagonalmente en triángulos, y el número de triángulos será igual norte- 2 (esta partición es una triangulación con vértices en los vértices norte-gón).

b) Deje que se marque el límite del polígono. r puntos (incluidos todos los vértices), dentro - más i agujas. Luego se realiza una triangulación con vértices en los puntos marcados, y el número de triángulos de dicha triangulación será igual.

Por supuesto, a) es un caso especial de b), cuando.

La validez de este teorema se desprende de las siguientes afirmaciones.

1) Desde el vértice del ángulo mayor norte-gon () siempre es posible dibujar una diagonal que se encuentre completamente dentro del polígono.

2) si norte-el cuadrado se corta en diagonal r-cuadrado y q-gon, entonces.

3) Suma de ángulos norte-gon es igual.

4) Cualquiera norte-un triángulo se puede cortar en diagonal en triángulos.

5) Para cualquier triángulo, dentro y en cuyo borde están marcados varios puntos (incluidos sus tres vértices), existe una triangulación con vértices en los puntos marcados.

6) Lo mismo ocurre con cualquiera. norte-gon.

7) El número de triángulos de triangulación es igual a, donde i Y r- número de puntos marcados, respectivamente, dentro y en el borde del polígono. Llamemos a la partición norte-gon en varios polígonos es correcto si cada vértice de uno de los polígonos de la partición sirve como vértice de todos los demás polígonos de la partición a la que pertenece. 8) Si desde los vértices k-gonos en los que se dividen de la forma correcta norte-gón, i los vértices se encuentran dentro y r- en la frontera norte-gon, entonces la cantidad k-los gons son iguales

9) Si los puntos del plano y los segmentos con extremos en estos puntos forman un polígono correctamente dividido en polígonos, entonces (figura 1.38)

De los teoremas 1 y 2 se deduce la fórmula del pico:

1.5 Teorema de Pitágoras sobre la suma de las áreas de cuadrados construidos sobre los lados de un triángulo rectángulo

Teorema. La suma de las áreas de los cuadrados construidos sobre los lados de un triángulo rectángulo es igual al área del cuadrado construido sobre la hipotenusa de este triángulo. Dejar abecedario(figura 1.39) es un triángulo rectángulo, y BDEA, AFGE Y BCKH- cuadrados construidos sobre sus catetos y su hipotenusa; debes demostrar que la suma de las áreas de los dos primeros cuadrados es igual al área del tercer cuadrado.

llevemos a cabo Sol. luego cuadrado BCKH se dividirá en dos rectángulos. Demostremos que el rectángulo BLMH igual a un cuadrado BDEA, y el rectángulo LCKM igual a un cuadrado AFGC.

Dibujemos líneas auxiliares. corriente continua Y UN. Considere los triángulos DCB Y ABH. Triángulo DCB tener una base BD, común con cuadrado BDEA, y la altura CN, igual a la altura AB de este cuadrado es igual a la mitad del cuadrado. Triángulo AVN tener una base VN, común con rectángulo BLMH y altura Arkansas, igual a la altura LICENCIADO EN DERECHO. de este rectángulo, igual en tamaño a su mitad. Comparando estos dos triángulos entre sí, encontramos que tienen BD = Virginia Y BC = VN(como los lados de un cuadrado);

Además, DCB = AVN, ya que cada uno de estos ángulos consta de una parte común: abecedario y ángulo recto. entonces triangulos AVN Y BCD son iguales. Se deduce que el rectángulo BLMN igual a un cuadrado BDEA. De la misma manera se demuestra que el rectángulo LGKM igual a un cuadrado AFGC. De ello se deduce que el cuadrado VSKN igual a la suma de cuadrados BDEA Y AFGC.

Cálculo del área de una figura.

método de selección

Trabajo de un estudiante de 5B de la escuela secundaria n.º 23 de MBOU en Irkutsk

Balsukova Alexandra

Responsable: Khodyreva T.G.

2014

Cálculo del área de una figura. método de selección

Objeto de estudio : problemas en papel cuadriculado

Tema de investigación : problemas de cálculo del área de un polígono en papel cuadriculado, métodos y técnicas para resolverlos.

Métodos de investigación : comparación, generalización, analogías, estudio de literatura y recursos de Internet, análisis de información.

Propósito del estudio:

elija la información principal, interesante y comprensible

Analizar y sistematizar la información recibida.

Encuentra diferentes métodos y técnicas para resolver problemas en papel cuadriculado.

consulte las fórmulas para calcular las áreas de figuras geométricas utilizando la fórmula Pick

Crear una presentación electrónica del trabajo para presentar el material recopilado.

La geometría es el medio más poderoso para agudizar nuestras facultades mentales y permitirnos pensar y razonar correctamente.

(G. Galileo)

Relevancia del tema.

La pasión por las matemáticas a menudo comienza pensando en un problema. Entonces, al estudiar el tema "Área de polígonos", surge la pregunta de si existen problemas que sean diferentes de los problemas discutidos en el libro de texto. Estos problemas incluyen problemas sobre papel cuadriculado. ¿Cuál es la peculiaridad de tales problemas? ¿Existen métodos y técnicas especiales para resolver problemas en papel cuadriculado? Durante una lección de matemáticas, el profesor nos presentó un método interesante para calcular polígonos. Comencé a estudiar literatura y recursos de Internet sobre este tema. Parecería que se puede encontrar algo fascinante en un plano cuadriculado, es decir, en una hoja de papel interminable, alineada en cuadrados idénticos. Resulta que las tareas asociadas con el papel cuadriculado son bastante diversas. Aprendí a calcular el área de polígonos dibujados en una hoja de papel a cuadros. Para muchos problemas en papel cuadriculado no existe una regla general para resolverlos ni métodos y técnicas específicos. Esta es su propiedad que determina su valor para el desarrollo no de una habilidad o destreza académica específica, sino en general la capacidad de pensar, reflexionar, analizar, buscar analogías, es decir, estas tareas desarrollan habilidades de pensamiento en su sentido más amplio.

Y también aprendí que tales tareas se consideran en los materiales de prueba y medición de la Academia Estatal de Ciencias y del Examen Estatal Unificado. Por lo tanto, considero que estudiar este material es útil para aplicarlo no solo en el proceso educativo posterior, sino también para resolver problemas no estándar de la Olimpiada.

2.Concepto de área

Cuadrado- una característica numérica de una figura geométrica bidimensional, que muestra el tamaño de esta figura. Históricamente, el cálculo del área se llamaba . Una figura que tiene área se llama al cuadrado .

Área de una figura plana en términos de geometría.

1. Cuadrado-medida de una figura plana con relación a una figura estándar, que es un cuadrado de lado igual a una unidad de longitud.

2. Cuadrado- una característica numérica atribuida a figuras planas de una determinada clase (por ejemplo, polígonos). El área de un cuadrado con un lado igual a una unidad de longitud, considerada igual a una unidad de área

3. Cuadrado- una cantidad positiva cuyo valor numérico tiene las siguientes propiedades:

 Figuras iguales tienen áreas iguales;

 Si una figura se divide en partes que son figuras simples (es decir, aquellas que se pueden dividir en un número finito de triángulos planos), entonces el área de esta figura es igual a la suma de las áreas de sus partes;

 El área de un cuadrado con un lado igual a una unidad de medida es igual a uno.

Por tanto, podemos concluir que el área no es una cantidad específica, sino que solo da alguna característica condicional de cualquier figura plana. Para encontrar el área de una figura arbitraria, debes determinar cuántos cuadrados con un lado igual a una unidad de longitud contiene. Por ejemplo, tomemos un rectángulo en el que cabe un centímetro cuadrado exactamente 6 veces. Esto significa que el área del rectángulo es de 6 cm 2.

La elección del área de un cuadrado con un lado igual a la unidad de medida como unidad mínima de medida de todas las áreas no es accidental. Este es el resultado de un acuerdo entre personas, que surgió en el curso de una selección "natural" centenaria. Además, hubo otras propuestas para una unidad de medida. Así, por ejemplo, se propuso tomar como unidad el área de un triángulo equilátero (es decir, cualquier figura plana podría representarse como la “suma” de un cierto número de triángulos equiláteros), lo que conduciría a una cambio en la representación numérica de las áreas.

Por lo tanto, las fórmulas para calcular áreas aparecieron en matemáticas y el hombre no las comprendió de inmediato; Muchos científicos viven en diferentes épocas y diferentes países. (Las fórmulas incorrectas no encontraron lugar en la ciencia y desaparecieron en el olvido). Las verdaderas fórmulas fueron completadas, corregidas y fundamentadas durante miles de años hasta que nos llegaron en su forma moderna.

Lo mismo medición de área Consiste en comparar el área de una figura determinada con el área de la figura tomada como unidad de medida. Como resultado de la comparación, se obtiene un cierto número: el valor numérico del área de una figura determinada. Este número muestra cuántas veces el área de una figura determinada es mayor (o menor) que el área de la figura tomada como unidad de medida del área.

t Así, podemos concluir que el área es una cantidad artificial, históricamente introducida por el hombre para medir alguna propiedad de una figura plana. La necesidad de introducir dicho valor estuvo determinada por la creciente necesidad de saber qué tan grande es un territorio determinado, cuánto grano se necesita para sembrar un campo o calcular la superficie del suelo para decorar baldosas ornamentales.

fórmula de elección

Para estimar el área de un polígono en papel cuadriculado, basta con contar cuántas celdas cubre este polígono (tomamos el área de una celda como uno). Más precisamente, siS es el área del polígono, B es el número de celdas que se encuentran completamente dentro del polígono y G es el número de celdas que tienen un interior. Consideraremos sólo aquellos polígonos cuyos vértices se encuentren en los nodos del papel cuadriculado, aquellos donde las líneas de la cuadrícula del polígono se cruzan con al menos un punto común.

El área de cualquier triángulo dibujado en papel cuadriculado se puede calcular fácilmente representándola como la suma o diferencia de las áreas de triángulos rectángulos y rectángulos cuyos lados siguen las líneas de la cuadrícula que pasan por los vértices del triángulo dibujado.

Para calcular el área de dicho polígono, puedes utilizar el siguiente teorema:

Teorema . Dejar - el número de puntos enteros dentro del polígono, - el número de puntos enteros en su límite, - su área. Entonces es justofórmula de elección:

Ejemplo. Para el polígono de la figura.l = 7 (puntos rojos), 9 (puntos verdes) entoncesS = 7+ 9/2 -1 = 10,5 unidades cuadradas.

teorema de pick- resultado clásico Y .

El área de un triángulo con vértices en los nodos y que no contiene nodos ni en el interior ni en los lados (excepto los vértices) es 1/2. Este hecho.

3. Historia

La fórmula de Pick fue descubierta por el matemático austriaco Georg Alexander (1859-1942) en . A la edad de 16 años, Georg se graduó de la escuela y entró en la. A los 20 años recibió el derecho a enseñar física y matemáticas. En 1884 Peake partió hacia A . Allí conoció a otro de los estudiantes de Klein,. Posteriormente, en 1885, regresó a, donde pasó el resto de su carrera científica.

Georg Pieck era amigo de Einstein. Peake y Einstein no sólo tenían intereses científicos comunes, sino que también sentían pasión por la música. Pick, que tocaba en un cuarteto formado por profesores universitarios, introdujo a Einstein en las sociedades científicas y musicales de Praga.

La gama de intereses matemáticos de Peake era extremadamente amplia. En particular, cuentan con más de 50 artículos científicos. El teorema de Pick para calcular el área de un polígono, descubierto por él en 1899, se hizo ampliamente conocido. En Alemania, este teorema está incluido en los libros de texto escolares.

4.Aplicaciones de la fórmula Pick

La fórmula de Pick se utiliza no solo para calcular las áreas de polígonos, sino también para resolver muchos problemas a nivel de Olimpiada.

Algunos ejemplos del uso de la fórmula Pick al resolver problemas:

1) El rey del ajedrez caminó alrededor de un tablero de 8 × 8 celdas, visitando cada una

campo de la casa exactamente una vez y con el último movimiento volviendo al original

campo. Una línea discontinua que conecta secuencialmente los centros de los campos que

pasó el rey, no tiene intersecciones propias. ¿Qué área puede

limitar esta línea discontinua? (El lado de la celda es 1.)

De la fórmula de Peak se deduce inmediatamente que el área limitada por el lo-

maná, igual a 64/2 − 1 = 31; aquí los nodos de la red son los centros 64

campos y, por condición, todos se encuentran en el límite del polígono. Entonces

Por lo tanto, aunque hay bastantes “trayectorias” del rey, todas son

polígonos unidos de áreas iguales.

Tareas de los materiales de prueba y medición de la Agencia Estatal de Exámenes y el Examen Estatal Unificado

Tarea B3

Encuentre el área de la figura representada en papel cuadriculado con un tamaño de celda de 1 cm 1 cm (ver figura). Da tu respuesta en centímetros cuadrados.

4.Conclusión

Durante el proceso de investigación, estudié literatura de referencia y divulgación científica. Aprendí que el problema de encontrar el área de un polígono con vértices en los nodos de la cuadrícula llevó al matemático austriaco Pieck a demostrar la notable fórmula de Pieck en 1899.

Como resultado de mi trabajo, amplié mis conocimientos sobre la resolución de problemas en papel cuadriculado, determiné por mí mismo la clasificación de los problemas en estudio y me convencí de su diversidad.

Aprendí a calcular las áreas de polígonos dibujados en una hoja de papel a cuadros. Las tareas consideradas tienen diferentes niveles de dificultad, desde las simples hasta las olímpicas. Todos pueden encontrar entre ellos tareas de un nivel de complejidad factible, a partir de las cuales será posible pasar a resolver otras más difíciles.

Llegué a la conclusión de que el tema que me interesaba era bastante multifacético, los problemas en papel cuadriculado eran variados y los métodos y técnicas para resolverlos también eran variados. Por eso decidimos seguir trabajando en esta dirección.

5. Literatura utilizada:

1. Vasil'ev N. B. Alrededor de la fórmula Pick // Quantum. - 1974. - No. 12

2. K o k e P r a s o l o v V. V. Problemas de planimetría. - M.: MTsNMO, 2006.t e r G.S.M. Introducción a la geometría. - M.: Ciencia, 1966

3.Roslova L.O., Sharygin I.F. Medidas. – M.: Editorial. "Mundo Abierto", 2005.

recursos de internet:

:

Comentarios para el trabajo

“Cálculo de áreas de figuras planas. Método de selección"

La consideración de este tema aumentará la actividad cognitiva del estudiante, quien posteriormente comenzará a ver la armonía del dibujo en las lecciones de geometría y dejará de percibir la geometría (y las matemáticas en general) como una ciencia aburrida.

Revisado por un profesor de matemáticas.

Jodyreva Tatyana Georgievna