Axioms of planimetry:
In different textbooks, the properties of lines and planes can be presented in different ways, in the form of an axiom, a corollary from it, a theorem, lemma, etc. Consider the textbook by Pogorelov A.V.
A straight line divides a plane into two half-planes.
0
From any half-line an angle with a given degree measure less than 180 can be plotted into a given half-plane. 0 , and only one.
Whatever a triangle is, there is an equal triangle in a given location relative to a given half-line.
Through a point not lying on a given line, it is possible to draw on the plane at most one straight line parallel to the given one.
Axioms of stereometry:
Whatever the plane, there are points that belong to this plane, and points that do not belong to this plane, and points that do not belong to it.
If two different planes have a common point, then they intersect along a straight line passing through this point.
If two different lines have a common point, then a plane can be drawn through them, and only one.
Whatever the line, there are points that belong to this line and points that do not belong to it.
Through any two points you can draw a straight line, and only one.
Of the three points on a line, one and only one lies between the other two.
Each segment has a certain length greater than zero. The length of a segment is equal to the sum of the lengths of the parts into which it is divided by any of its points.
A straight line belonging to a plane divides this plane into two half-planes.
Each angle has a certain degree measure greater than zero. The straight angle is 180 0 . The degree measure of an angle is equal to the sum of the degree measures of the angles into which it is divided by any ray passing between its sides.
On any half-line from its starting point, you can plot a segment of a given length, and only one.
From a half-line on the plane containing it, an angle with a given degree measure less than 180 can be plotted into a given half-plane 0 , and only one.
Whatever the triangle, there is an equal triangle in a given plane in a given location relative to a given half-line in that plane.
On a plane, through a given point that does not lie on a given line, it is possible to draw at most one straight line parallel to the given one.
Section
In space, two figures, for our case a plane and a polyhedron, can have the following relative positions: do not intersect, intersect at a point, intersect in a straight line and the plane intersects the polyhedron along its interior (Fig. 1), and at the same time form the following figures:
a) empty figure (do not intersect)
b) point
c) segment
d) polygon
If there is a polygon at the intersection of a polyhedron and a plane, then this polygoncalled a section of a polyhedron with a plane .
Fig.1
Definition. Section spatial body (for example, a polyhedron) is the figure resulting from the intersection of the body with a plane.
Cutting plane polyhedron let's call any plane on both sides of which there are points of a given polyhedron.
We will consider only the case when the plane intersects the polyhedron along its interior. In this case, the intersection of this plane with each face of the polyhedron will be a certain segment.
If the planes intersect in a straight line, then the straight line is calledfollowing one of these planes onto the other.
In general, the cutting plane of a polyhedron intersects the plane of each of its faces (as well as any other cutting plane of this polyhedron). It also intersects each of the lines on which the edges of the polyhedron lie.
The straight line along which the cutting plane intersects the plane of any face of the polyhedron is calledfollowing the cutting plane on the plane of this face, and the point at which the cutting plane intersects the line containing any edge of the polyhedron is calledfollowing the cutting plane onthis straight line. This point is also the trace of a line on the cutting plane. If the cutting plane directly intersects the face of the polyhedron, then we can talk about the trace of the cutting plane on the face, and, similarly, abouttrace of the cutting plane on the edge of the polyhedron, that is, about the trace of an edge on a cutting plane.
Since a straight line is uniquely determined by two points, to find the trace of a cutting plane on any other plane and, in particular, on the plane of any face of a polyhedron, it is sufficient to construct two common points of the planes
To construct the trace of a cutting plane, as well as to construct a section of a polyhedron with this plane, not only the polyhedron, but also the cutting plane must be specified. And the construction of the section plane depends on the specification of this plane. The main ways to define a plane, and in particular a cutting plane, are as follows:
three points not lying on the same line;
a straight line and a point not lying on it;
two parallel lines;
two intersecting lines;
a point and two intersecting lines;
Other ways of specifying a cutting plane are also possible.
Therefore, all methods for constructing sections of polyhedra can be divided into methods.
Methods for constructing sections of polyhedra
The method of sections of polyhedra in stereometry is used in construction problems. It is based on the ability to construct a section of a polyhedron and determine the type of section.
There are three main methods for constructing sections of polyhedra:
Axiomatic method:
Trace method.
Combined method.
Coordinate method.
Note that the trace method and the auxiliary section method are varietiesAxiomatic method for constructing sections.
We can also distinguish the following methods for constructing sections of polyhedra:
constructing a section of a polyhedron with a plane passing through a given point parallel to a given plane;
constructing a section passing through a given line parallel to another given line;
constructing a section passing through a given point parallel to two given intersecting lines;
constructing a section of a polyhedron with a plane passing through a given line perpendicular to a given plane;
constructing a section of a polyhedron with a plane passing through a given point perpendicular to a given straight line.
The main actions that make up the methods for constructing sections are finding the point of intersection of a line with a plane, constructing the line of intersection of two planes, constructing a straight line parallel to the plane, perpendicular to the plane. To construct a line of intersection of two planes, two of its points are usually found and a line is drawn through them. To construct the intersection point of a line and a plane, find a line in the plane that intersects the given one. Then the desired point is obtained at the intersection of the found line with the given one.
Let us consider separately the ones we have listedmethods for constructing sections of polyhedra:
Trace method.
Trace method is based (based on) the axioms of stereometry, the essence of the method is to construct an auxiliary line, which is an image of the line of intersection of the cutting plane with the plane of any face of the figure. It is most convenient to construct an image of the line of intersection of the cutting plane with the plane of the lower base. This linecalled the main trace of the cutting plane . Using a trace, it is easy to construct images of points of the cutting plane located on the lateral edges or faces of the figure. Consistently connecting the images of these points, we obtain an image of the desired section.
Note that that when constructing the main trace of a cutting plane, the following statement is used.
If the points belong to the cutting plane and do not lie on the same straight line, and their projection (central or parallel) onto the plane chosen as the main one, the points are respectively then the points of intersection of the corresponding lines, that is, the points and lie on the same line (Fig. 1, a, b).

Fig.1.a Fig.1.b
This straight line is the main trace of the cutting plane. Since the points lie on the main trace, to construct it it is enough to find two points out of these three.
Method of auxiliary sections.
This method of constructing sections of polyhedra is quite universal. In cases where the desired trace (or traces) of the cutting plane is outside the drawing, this method even has certain advantages. At the same time, it should be borne in mind that constructions performed using this method often turn out to be “crowded.” However, in some cases the method of auxiliary sections turns out to be the most rational.
Combined method
The essence of the combined method for constructing sections of polyhedra is the application of theorems on the parallelism of lines and planes in space in combination with the axiomatic method.
Coordinate method for constructing sections.
The essence of the coordinate method is to calculate the coordinates of the intersection points of the edges or polyhedron with the cutting plane, which is specified by the equation of the plane. The cutting plane equation is calculated based on the problem conditions.
Note , that this method of constructing a section of a polyhedron is acceptable for a computer, since it is associated with a large amount of calculations and therefore this method is advisable to implement using a computer.
Our main task will be to construct a section of a polyhedron with a plane, i.e. in constructing the intersection of these two sets.
Construction of sections of polyhedra
First of all, we note that the section of a convex polyhedron is a convex flat polygon, the vertices of which, in the general case, are the points of intersection of the cutting plane with the edges of the polyhedron, and the sides with its faces.
Examples of constructing sections:
The methods for defining a section are very diverse. The most common of them is the method of defining a cutting plane by three points that do not lie on the same straight line.
Example 1.
For parallelepiped ABCDA 1
B 1
C 1
D 1
. Construct a section passing through points M, N, L.
Solution:
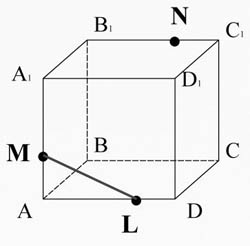
Connect points M and L lying in plane AA 1 D 1 D.

Let us intersect the line ML (belonging to the section) with the edge A 1 D 1 1 D 1 D. Get point X 1 .

Point X1 lies on edge A 1 D 1 , and hence the plane A 1 B 1 C 1 D 1 , we connect it with a stitch N lying in the same plane.
X 1 N intersects edge A 1 B 1 at point K.

Connect points K and M lying in the same plane AA 1 B 1 B.
Let's find the straight line of intersection of the section plane with the DD plane 1
C 1
C:
Let us intersect the line ML (belonging to the section) with the edge DD 1 , they lie in the same plane AA 1 D 1 D, we get point X 2 .
Let us intersect the line KN (belonging to the section) with the edge D 1
C 1
, they lie in the same plane A 1
B 1
C 1
D 1
, we get point X3;

Points X2 and X3 lie in the DD plane 1 C 1 C. Draw a straight line X 2 X 3 , which intersects edge C 1 C at point T, and edge DC at point P. And connect points L and P lying in the plane ABCD.
Thus, the problem is considered solved if all the segments along which the plane intersects the faces of the polyhedron are found, which is what we did. MKNTPL - the required section.
Note. This same problem of constructing a section can be solved using the property of parallel planes.
From the above, you can create an algorithm (rule) for solving problems of this type.
Rules for constructing sections of polyhedra:
draw straight lines through points lying in the same plane;
We are looking for direct intersections of the section plane with the faces of the polyhedron, for this:

Example 2. DL, M
Let's solve using the axiomatic method:
Let's draw an auxiliary planeDKM, which intersects edges AB and BC at points E andF(progress of the solution in Fig. 2.). Let's construct a “trace” of the CM of the section plane on this auxiliary plane, find the intersection point of the CM and EF– point P. Point P, likeL, lies in the ABC plane, and it is possible to draw a straight line along which the section plane intersects the ABC plane (“trace” of the section in the ABC plane).



Example 3. On the edges AB and AD of the MABCD pyramid, we define points P and Q, respectively, the midpoints of these edges, and on the edge MC we define a point R. Let us construct a section of the pyramid with a plane passing through points P, Q and R.
We will carry out the solution using a combined method:
1). It is clear that the main trace of the plane PQR is the straight line PQ.
2). Let us find the point K at which the MAC plane intersects the straight line PQ. Points K and R belong to both the PQR plane and the MAC plane. Therefore, by drawing the straight line KR, we get the line of intersection of these planes.
3). Let's find the point N=AC BD, draw a straight line MN and find the point F=KR MN.
4). Point F is the common point of the planes PQR and MDB, that is, these planes intersect along a straight line passing through point F. At the same time, since PQ is the midline of the triangle ABD, then PQ is parallel to BD, that is, the line PQ is parallel to the plane MDB. Then the plane PQR passing through the straight line PQ intersects the plane MDB along a straight line parallel to the straight line PQ, that is, parallel and straight BD. Therefore, in the plane MDB through point F we draw a line parallel to line BD.
5). Further constructions are clear from the figure. As a result, we obtain the polygon PQD"RB" - the desired section
Let's consider the cross sections of the prism
for simplicity, that is, convenience of logical thinking, let’s consider the sections of the cube (Fig. 3.a):

Rice. 3.a

Sections of a prism with planes parallel to the side edges are parallelograms. In particular, diagonal sections are parallelograms (Fig. 4).
Def. Diagonal section A prism is cut by a plane passing through two lateral edges that do not belong to the same face.
The polygon resulting from a diagonal section of a prism is a parallelogram. Question about the number of diagonal sectionsn-angle prism is more difficult than the question of the number of diagonals. There will be as many sections as there are diagonals at the base. We know that a convex prism has convex polygons at its bases, and a convex prismn-gon of diagonals. And so we can say that there are half as many diagonal sections as diagonals.
Note: When constructing sections of a parallelepiped in the figure, one should take into account the fact that if a cutting plane intersects two opposite faces along some segments, then these segments are parallel “by the property of a parallelepiped, i.e. The opposite faces of the parallelepiped are parallel and equal.”
We will give answers to frequently asked questions:
What polygons are obtained when a cube is cut by a plane?
"triangle, quadrangle, pentagon, hexagon."
Can a cube be cut by a plane into a heptagon? What about the octagon?
"they can't."
3) The question arises: what is the largest number of sides of a polygon obtained by cutting a polyhedron with a plane?
The largest number of sides of a polygon obtained by cutting a polyhedron by a plane is equal to the number of faces of the polyhedron .
Example 3. Construct a cross section of prism A 1 B 1 C 1 D 1 ABCD by a plane passing through three points M, N, K.
Let us consider the case of the location of points M, N, K on the surface of the prism (Fig. 5).
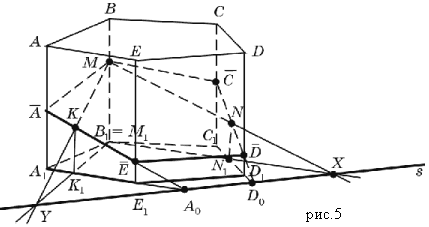
Consider the case: In this case, it is obvious that M1 = B1.
Construction:
Example 4. Construct a section of the parallelepiped ABCDA 1 B 1 C 1 D 1 a plane passing through points M, N, P (the points are indicated in the drawing (Fig. 6)).
Solution:

Rice. 6
Points N and P lie in the section plane and in the plane of the lower base of the parallelepiped. Let's construct a straight line passing through these points. This straight line is the trace of the cutting plane onto the plane of the base of the parallelepiped.
Let us continue the straight line on which side AB of the parallelepiped lies. Lines AB and NP intersect at some point S. This point belongs to the section plane.
Since point M also belongs to the section plane and intersects line AA 1 at some point X.
Points X and N lie in the same plane of face AA 1 D 1 D, connect them and get straight line XN.
Since the planes of the faces of the parallelepiped are parallel, then through the point M we can draw a straight line to the face A 1 B 1 C 1 D 1 , parallel to the line NP. This line will intersect side B 1 WITH 1 at point Y.
Similarly, we draw straight line YZ, parallel to straight line XN. We connect Z with P and get the desired section - MYZPNX.
Sections of a pyramid by planes passing through its apex are triangles. In particular, triangles are diagonal sections. These are sections by planes passing through two non-adjacent lateral edges of the pyramid.
Example 4.
Construct a cross section of the pyramid ABCDplane passing through points K,L,
M.

Solution:

Let's draw another auxiliary planeDCKand construct the intersection point BLAndDK – point E. This point belongs to both auxiliary planes (Fig. 7, b);
Let's find the point of intersection of the segmentsL.M.and EC (these segments lie in the planeBLC, Fig. 7, c) – pointF. DotFlies in the section plane and in the planeDCK;
Let's make a directKFand find the point of intersection of this line withDC– pointN(dotNbelongs to the section). QuadrangleKLNM– the required section.
Let's solve this same example differently .
Let us assume that at points K,L, and M constructed sectionKLNM(Fig. 7). Let us denote byFpoint of intersection of the diagonals of a quadrilateralKLNM. Let's make a directDFand denote byF 1
its point of intersection with edge ABC. DotF 1
coincides with the point of intersection of straight lines AM and SC (F 1
simultaneously belongs to the planes AMDAndDSK). Full stopF 1
easy to build. Next we build a pointFas a point of intersectionDF 1
AndL.M.. Next we find the pointN.

The technique considered is calledinternal design method . (For our case we are talking about central design. QuadrangleKMSA is the projection of a quadrilateralKMNLfrom pointD. In this case, the point of intersection of the diagonalsKMNL– pointF– goes to the point of intersection of the diagonals of the quadrilateralKMSA - pointF 1 .
Sectional area of a polyhedron.
The problem of calculating the cross-sectional area of a polyhedron is usually solved in several stages. If the problem states that a section has been constructed (or that a cutting plane has been drawn, etc.), then at the first stage of the solution the type of figure obtained in the section is determined.
This must be done to select the appropriate formula for calculating the cross-sectional area. After the type of figure obtained in the section has been clarified and a formula has been selected for calculating the area of this figure, we proceed directly to the computational work.
In some cases, it may be easier if, without figuring out the type of figure obtained in the section, you go straight to calculating its area using the formula that follows from the theorem.
Theorem on the area of the orthogonal projection of a polygon: The area of the orthogonal projection of a polygon onto a plane is equal to the product of its area and the cosine of the angle between the plane of the polygon and the projection plane: .
The correct formula for calculating the sectional area is: where is the area of the orthogonal projection of the figure obtained in the section, and this is the angle between the cutting plane and the plane onto which the figure is projected. With this solution, it is necessary to construct an orthogonal projection of the figure obtained in the section and calculate
If the problem statement states that a section needs to be constructed and the area of the resulting section must be found, then at the first stage one should justifiably construct the given section, and then, naturally, determine the type of figure obtained in the section, etc.
Let us note the following fact: since sections of convex polyhedra are constructed, the section polygon will also be convex, so its area can be found by dividing it into triangles, that is, the section area is equal to the sum of the areas of the triangles from which it is composed.
Task 1.
– a regular triangular pyramid with a side of the base equal and a height equal to Construct a section of the pyramid with a plane passing through the points where is the middle of the side, and find its area (Fig. 8).
Solution.
The cross section of a pyramid is a triangle. Let's find its area.
Since the base of the pyramid is an equilateral triangle and the point is the midpoint of the side, it is the height and then, .
The area of a triangle can be found:
Task 2.
The lateral edge of a regular prism is equal to the side of the base. Construct sections of a prism with planes passing through a pointA, perpendicular to the straight line If we find the area of the resulting cross-section of the prism.
Solution.
Let's construct the given section. Let's do this from purely geometric considerations, for example, as follows.
In a plane passing through a given line and a given point, draw a line perpendicular to the line through this point (Fig. 9). For this purpose, let us use the fact that in the triangle that is, its median is also the height of this triangle. So it's straight.
Through the point we draw another line perpendicular to the line. Let us draw it, for example, in a plane passing through a straight line. It is clear that this line is the straight line
So, two intersecting lines are constructed, perpendicular to the line. These lines define a plane passing through a point perpendicular to the line, that is, a secant plane is specified.
Let's construct a section of the prism with this plane. Note that since, the line is parallel to the plane. Then the plane passing through the straight line intersects the plane along a straight line parallel to the straight line, that is, a straight line. Let's draw a straight line through the point and connect the resulting point with a dot.
Quadrilateral given section. Let's determine its area.
It is clear that a quadrilateral is a rectangle, that is, its area is
rice. 9
Do you know what is called the section of polyhedra by a plane? If you still doubt the correctness of your answer to this question, you can check yourself quite simply. We suggest you take a short test below.
Question. What is the number of the figure that shows the section of a parallelepiped by a plane?
So, the correct answer is in Figure 3.
If you answer correctly, it confirms that you understand what you are dealing with. But, unfortunately, even the correct answer to a test question does not guarantee you the highest grades in lessons on the topic “Sections of polyhedra.” After all, the most difficult thing is not recognizing sections in finished drawings, although this is also very important, but their construction.
To begin with, let us formulate the definition of a section of a polyhedron. So, a section of a polyhedron is a polygon whose vertices lie on the edges of the polyhedron, and whose sides lie on its faces.
Now let’s practice quickly and accurately constructing intersection points  a given straight line with a given plane. To do this, let's solve the following problem.
a given straight line with a given plane. To do this, let's solve the following problem.
Construct the intersection points of straight line MN with the planes of the lower and upper bases of the triangular prism ABCA 1 B 1 C 1, provided that point M belongs to the side edge CC 1, and point N belongs to edge BB 1.
Let's start by extending straight line MN in both directions in the drawing (Fig. 1). Then, in order to obtain the intersection points required by the problem, we extend the lines lying in the upper and lower bases. And now comes the most difficult moment in solving the problem: which lines in both bases need to be extended, since each of them has three lines.
In order to correctly complete the final step of construction, it is necessary to determine which of the direct bases are in the same plane as the straight line MN of interest to us. In our case, this is straight CB in the lower and C 1 B 1 in the upper bases. And it is precisely these that we extend until they intersect with the straight line NM (Fig. 2).

The resulting points P and P 1 are the points of intersection of the straight line MN with the planes of the upper and lower bases of the triangular prism ABCA 1 B 1 C 1 .
After analyzing the presented problem, you can proceed directly to constructing sections of polyhedra. The key point here will be reasoning that will help you arrive at the desired result. As a result, we will eventually try to create a template that will reflect the sequence of actions when solving problems of this type.
So, let's consider the following problem. Construct a section of a triangular prism ABCA 1 B 1 C 1 by a plane passing through points X, Y, Z belonging to edges AA 1, AC and BB 1, respectively.
Solution: Let's draw a drawing and determine which pairs of points lie in the same plane.
 Pairs of points X and Y, X and Z can be connected, because they lie in the same plane.
Pairs of points X and Y, X and Z can be connected, because they lie in the same plane.
Let's construct an additional point that will lie on the same face as point Z. To do this, we will extend the lines XY and CC 1, because they lie in the plane of the face AA 1 C 1 C. Let's call the resulting point P.
Points P and Z lie in the same plane - in the plane of the face CC 1 B 1 B. Therefore, we can connect them. The straight line PZ intersects the edge CB at a certain point, let's call it T. Points Y and T lie in the lower plane of the prism, connect them. Thus, the quadrilateral YXZT was formed, and this is the desired section. 
Let's summarize. To construct a section of a polyhedron with a plane, you must:
1) draw straight lines through pairs of points lying in the same plane.
2) find the lines along which the section planes and faces of the polyhedron intersect. To do this, you need to find the intersection points of a straight line belonging to the section plane with a straight line lying in one of the faces.
The process of constructing sections of polyhedra is complicated because it is different in each specific case. And no theory describes it from beginning to end. In fact, there is only one sure way to learn how to quickly and accurately construct sections of any polyhedra - this is constant practice. The more sections you build, the easier it will be for you to do this in the future.
blog.site, when copying material in full or in part, a link to the original source is required.
Do you know what is called the section of polyhedra by a plane? If you still doubt the correctness of your answer to this question, you can check yourself quite simply. We suggest you take a short test below.
Question. What is the number of the figure that shows the section of a parallelepiped by a plane?
So, the correct answer is in Figure 3.
If you answer correctly, it confirms that you understand what you are dealing with. But, unfortunately, even the correct answer to a test question does not guarantee you the highest grades in lessons on the topic “Sections of polyhedra.” After all, the most difficult thing is not recognizing sections in finished drawings, although this is also very important, but their construction.
To begin with, let us formulate the definition of a section of a polyhedron. So, a section of a polyhedron is a polygon whose vertices lie on the edges of the polyhedron, and whose sides lie on its faces.
Now let’s practice quickly and accurately constructing intersection points  a given straight line with a given plane. To do this, let's solve the following problem.
a given straight line with a given plane. To do this, let's solve the following problem.
Construct the intersection points of straight line MN with the planes of the lower and upper bases of the triangular prism ABCA 1 B 1 C 1, provided that point M belongs to the side edge CC 1, and point N belongs to edge BB 1.
Let's start by extending straight line MN in both directions in the drawing (Fig. 1). Then, in order to obtain the intersection points required by the problem, we extend the lines lying in the upper and lower bases. And now comes the most difficult moment in solving the problem: which lines in both bases need to be extended, since each of them has three lines.
In order to correctly complete the final step of construction, it is necessary to determine which of the direct bases are in the same plane as the straight line MN of interest to us. In our case, this is straight CB in the lower and C 1 B 1 in the upper bases. And it is precisely these that we extend until they intersect with the straight line NM (Fig. 2).

The resulting points P and P 1 are the points of intersection of the straight line MN with the planes of the upper and lower bases of the triangular prism ABCA 1 B 1 C 1 .
After analyzing the presented problem, you can proceed directly to constructing sections of polyhedra. The key point here will be reasoning that will help you arrive at the desired result. As a result, we will eventually try to create a template that will reflect the sequence of actions when solving problems of this type.
So, let's consider the following problem. Construct a section of a triangular prism ABCA 1 B 1 C 1 by a plane passing through points X, Y, Z belonging to edges AA 1, AC and BB 1, respectively.
Solution: Let's draw a drawing and determine which pairs of points lie in the same plane.
 Pairs of points X and Y, X and Z can be connected, because they lie in the same plane.
Pairs of points X and Y, X and Z can be connected, because they lie in the same plane.
Let's construct an additional point that will lie on the same face as point Z. To do this, we will extend the lines XY and CC 1, because they lie in the plane of the face AA 1 C 1 C. Let's call the resulting point P.
Points P and Z lie in the same plane - in the plane of the face CC 1 B 1 B. Therefore, we can connect them. The straight line PZ intersects the edge CB at a certain point, let's call it T. Points Y and T lie in the lower plane of the prism, connect them. Thus, the quadrilateral YXZT was formed, and this is the desired section. 
Let's summarize. To construct a section of a polyhedron with a plane, you must:
1) draw straight lines through pairs of points lying in the same plane.
2) find the lines along which the section planes and faces of the polyhedron intersect. To do this, you need to find the intersection points of a straight line belonging to the section plane with a straight line lying in one of the faces.
The process of constructing sections of polyhedra is complicated because it is different in each specific case. And no theory describes it from beginning to end. In fact, there is only one sure way to learn how to quickly and accurately construct sections of any polyhedra - this is constant practice. The more sections you build, the easier it will be for you to do this in the future.
website, when copying material in full or in part, a link to the source is required.
The task itself usually sounds like this: "build a natural view of a section figure". Of course, we decided not to leave this issue aside and try, if possible, to explain how the inclined section is constructed.
In order to explain how an inclined section is constructed, I will give several examples. I will, of course, start with the elementary ones, gradually increasing the complexity of the examples. I hope that after analyzing these examples of section drawings, you will understand how it is done and will be able to complete your study assignment yourself.
Let's consider a “brick” with dimensions 40x60x80 mm and an arbitrary inclined plane. The cutting plane cuts it at points 1-2-3-4. I think everything is clear here.
Let's move on to constructing a natural view of the section figure.
1. First of all, let's draw the section axis. The axis should be drawn parallel to the section plane - parallel to the line into which the plane is projected in the main view - usually it is in the main view that the task for construction of an inclined section(Further I will always mention the main view, keeping in mind that this almost always happens in educational drawings).
2. On the axis we plot the length of the section. In my drawing it is designated as L. The size L is determined in the main view and is equal to the distance from the point of entry of the section into the part to the point of exit from it.
3. From the resulting two points on the axis, perpendicular to it, we plot the width of the section at these points. The width of the section at the point of entry into the part and at the point of exit from the part can be determined in the top view. In this case, both segments 1-4 and 2-3 are equal to 60 mm. As you can see from the picture above, the edges of the section are straight, so we simply connect our two resulting segments, obtaining a rectangle 1-2-3-4. This is the natural appearance of the cross section of our brick by an inclined plane.

Now let's complicate our part. Let's place a brick on a base 120x80x20 mm and add stiffening ribs to the figure. Let's draw a cutting plane so that it passes through all four elements of the figure (through the base, brick and two stiffeners). In the picture below you can see three views and a realistic image of this part.

Let's try to build a natural view of this inclined section. Let's start again with the section axis: draw it parallel to the section plane indicated in the main view. On it we plot the length of the section equal to A-E. Point A is the entry point of the section into the part, and in a particular case, the entry point of the section into the base. The exit point from the base is point B. Mark point B on the section axis. In a similar way, we mark the entry and exit points to the edge, to the “brick” and to the second edge. From points A and B, perpendicular to the axis, we will lay out segments equal to the width of the base (40 in each direction from the axis, 80 mm in total). Let's connect the extreme points - we get a rectangle, which is a natural cross-section of the base of the part.

Now it’s time to build a piece of the section, which is a section of the edge of the part. From points B and C we will put perpendiculars of 5 mm in each direction - we will get segments of 10 mm. Let's connect the extreme points and get a section of the rib.

From points C and D we lay out perpendicular segments equal to the width of the “brick” - completely similar to the first example of this lesson.

By setting aside perpendiculars from points D and E equal to the width of the second edge and connecting the extreme points, we obtain a natural view of its section.

All that remains is to erase the jumpers between the individual elements of the resulting section and apply shading. It should look something like this:

If we divide the figure along a given section, we will see the following view:

I hope that you are not intimidated by the tedious paragraphs describing the algorithm. If you have read all of the above and still do not fully understand, how to draw an inclined section, I strongly advise you to pick up a piece of paper and a pencil and try to repeat all the steps after me - this will almost 100% help you learn the material.
I once promised a continuation of this article. Finally, I am ready to present you with a step-by-step construction of an inclined section of a part, closer to the level of homework. Moreover, the inclined section is defined in the third view (the inclined section is defined in the left view)
or write down our phone number and tell your friends about us - someone is probably looking for a way to complete the drawings
or Create a note about our lessons on your page or blog - and someone else will be able to master drawing.
Yes, everything is fine, but I would like to see how to do the same thing on a more complex part, with chamfers and a cone-shaped hole, for example.
Thank you. Aren't the stiffening ribs hatched on the sections?
Exactly. They are the ones who do not hatch. Because these are the general rules for making cuts. However, they are usually shaded when making cuts in axonometric projections - isometry, dimetry, etc. When making inclined sections, the area related to the stiffener is also shaded.
Thank you, very accessible. Tell me, can an inclined section be done in the top view, or in the left view? If so, then I would like to see a simple example. Please.
It is possible to make such sections. But unfortunately I don’t have an example at hand right now. And there is another interesting point: on the one hand, there is nothing new there, but on the other hand, in practice such sections are actually more difficult to draw. For some reason, everything starts to get confused in the head and most students have difficulties. But don't give up!
Yes, everything is fine, but I would like to see how the same thing is done, but with holes (through and not through), otherwise they never turn into an ellipse in the head
help me with a complex problem
It's a pity that you wrote here. If you could write to us by email, maybe we could have time to discuss everything.
You explain well. What if one of the sides of the part is semicircular? There are also holes in the part.
Ilya, use the lesson from the section on descriptive geometry “Section of a cylinder by an inclined plane.” With its help you can figure out what to do with the holes (they are essentially cylinders too) and with the semicircular side.
I thank the author for the article! It’s brief and easy to understand. About 20 years ago I was gnawing on the granite of science, now I’m helping my son. I forgot a lot, but your article brought back a fundamental understanding of the topic. I’ll go figure out the inclined section of the cylinder)
Add your comment.
Today we’ll look again at how construct a section of a tetrahedron with a plane.
Let's consider the simplest case (mandatory level), when 2 points of the section plane belong to one face, and the third point belongs to another face.
Let us remind you algorithm for constructing sections of this type (case: 2 points belong to the same face).
1. We are looking for a face that contains 2 points of the section plane. Draw a straight line through two points lying on the same face. We find the points of its intersection with the edges of the tetrahedron. The part of the straight line that ends up in the face is the side of the section.
2. If the polygon can be closed, the section has been constructed. If it is impossible to close, then we find the point of intersection of the constructed line and the plane containing the third point.
 1. We see that points E and F lie on the same face (BCD), draw a straight line EF in the plane (BCD).
1. We see that points E and F lie on the same face (BCD), draw a straight line EF in the plane (BCD).  2. Find the point of intersection of the straight line EF with the edge of the tetrahedron BD, this is point H.
2. Find the point of intersection of the straight line EF with the edge of the tetrahedron BD, this is point H.
3. Now you need to find the point of intersection of the straight line EF and the plane containing the third point G, i.e. plane (ADC).
The straight line CD lies in the planes (ADC) and (BDC), which means it intersects the straight line EF, and point K is the point of intersection of the straight line EF and the plane (ADC).
4. Next, we find two more points lying in the same plane. These are points G and K, both lie in the plane of the left side face. We draw a line GK and mark the points at which this line intersects the edges of the tetrahedron. These are points M and L.
4. It remains to “close” the section, i.e. connect the points lying on the same face. These are points M and H, and also L and F. Both of these segments are invisible, we draw them with a dotted line.


 The cross-section turned out to be a quadrangle MHFL. All its vertices lie on the edges of the tetrahedron. Let's select the resulting section.
The cross-section turned out to be a quadrangle MHFL. All its vertices lie on the edges of the tetrahedron. Let's select the resulting section.
Now let's formulate "properties" of a correctly constructed section:
1. All vertices of a polygon, which is a section, lie on the edges of a tetrahedron (parallelepiped, polygon).
2. All sides of the section lie on the faces of the polyhedron.
3. Each face of a polygon can contain no more than one (one or none!) side of the section
