Invers matrixoversættelse. Invers matrix definition eksistens og unikhed

Lad der være en kvadratisk matrix af n. orden

Matrix A -1 kaldes omvendt matrix i forhold til matrix A, hvis A*A -1 = E, hvor E er identitetsmatrixen af ​​n'te orden.

Identitetsmatrix- sådan en firkantet matrix, hvor alle elementerne langs hoveddiagonalen, der går fra det øverste venstre hjørne til det nederste højre hjørne, er etaller, og resten er nuller, for eksempel:

Invers matrix kan eksistere kun for kvadratiske matricer dem. for de matricer, hvor antallet af rækker og kolonner falder sammen.

Sætning for eksistensbetingelsen for en invers matrix

For at en matrix skal have en invers matrix, er det nødvendigt og tilstrækkeligt, at den er ikke-singular.

Matrixen A = (A1, A2,...A n) kaldes ikke-degenereret, hvis kolonnevektorerne er lineært uafhængige. Antallet af lineært uafhængige kolonnevektorer i en matrix kaldes matrixens rang. Derfor kan vi sige, at for at en invers matrix skal eksistere, er det nødvendigt og tilstrækkeligt, at rangeringen af ​​matrixen er lig med dens dimension, dvs. r = n.

Algoritme til at finde den inverse matrix

1. Skriv matrix A i tabellen til løsning af ligningssystemer ved hjælp af Gauss-metoden og tildel matrix E til den til højre (i stedet for ligningernes højre side).
2. Brug Jordan-transformationer til at reducere matrix A til en matrix bestående af enhedssøjler; i dette tilfælde er det nødvendigt at transformere matrixen E samtidigt.
3. Om nødvendigt omarranger rækkerne (ligningerne) i den sidste tabel, så du under matrixen A i den oprindelige tabel får identitetsmatrixen E.
4. Skriv den inverse matrix A -1 ned, som er placeret i den sidste tabel under matrix E i den oprindelige tabel.

Eksempel 1

For matrix A, find den inverse matrix A -1

Løsning: Vi skriver matrix A og tildeler identitetsmatrix E til højre Ved hjælp af Jordan-transformationer reducerer vi matrix A til identitetsmatrix E. Beregningerne er angivet i tabel 31.1.

Lad os kontrollere rigtigheden af ​​beregningerne ved at gange den oprindelige matrix A og den inverse matrix A -1.

Som et resultat af matrixmultiplikation blev identitetsmatrixen opnået. Derfor er beregningerne udført korrekt.

Svar:

Løsning af matrixligninger

Matrixligninger kan se sådan ud:

AX = B, HA = B, AXB = C,

hvor A, B, C er de specificerede matricer, X er den ønskede matrix.

Matrixligninger løses ved at gange ligningen med inverse matricer.

For at finde matricen ud fra ligningen skal du for eksempel gange denne ligning med til venstre.

For at finde en løsning på ligningen skal du derfor finde den inverse matrix og gange den med matricen på højre side af ligningen.

Andre ligninger løses på samme måde.

Eksempel 2

Løs ligningen AX = B if

Løsning: Da den inverse matrix er lig med (se eksempel 1)

Matrixmetode i økonomisk analyse

Sammen med andre bruges de også matrix metoder. Disse metoder er baseret på lineær og vektor-matrix algebra. Sådanne metoder anvendes med det formål at analysere komplekse og multidimensionelle økonomiske fænomener. Oftest bruges disse metoder, når det er nødvendigt at foretage en sammenlignende vurdering af organisationers funktion og deres strukturelle opdelinger.

I processen med at anvende matrixanalysemetoder kan der skelnes mellem flere stadier.

På den første fase et system af økonomiske indikatorer er ved at blive dannet, og på grundlag heraf kompileres en matrix af indledende data, som er en tabel, hvor systemnumre vises i de enkelte rækker (i = 1,2,....,n), og i lodrette kolonner - antal indikatorer (j = 1,2,...,m).

På anden fase For hver lodret kolonne identificeres den største af de tilgængelige indikatorværdier, som tages som én.

Herefter divideres alle beløb afspejlet i denne kolonne med den største værdi, og der dannes en matrix af standardiserede koefficienter.

På tredje fase alle komponenter i matrixen er kvadratiske. Hvis de har forskellig betydning, er hver matrixindikator tildelt en vis vægtkoefficient k. Værdien af ​​sidstnævnte bestemmes af ekspertudtalelse.

På den sidste, fjerde etape fundet vurderingsværdier Rj er grupperet i rækkefølge efter deres stigning eller fald.

De skitserede matrixmetoder bør f.eks. bruges i en komparativ analyse af forskellige investeringsprojekter samt ved vurdering af andre økonomiske indikatorer for organisationers aktiviteter.

For at finde den inverse matrix online, skal du angive størrelsen på selve matrixen. For at gøre dette skal du klikke på "+" eller "-" ikonerne, indtil du er tilfreds med antallet af kolonner og rækker. Indtast derefter de nødvendige elementer i felterne. Nedenfor er knappen "Beregn" - ved at klikke på den får du svar på skærmen med en detaljeret løsning.

I lineær algebra skal man ret ofte beskæftige sig med processen med at beregne den inverse matrix. Den eksisterer kun for uudtrykte matricer og for kvadratiske matricer, forudsat at determinanten ikke er nul. I princippet er det ikke specielt svært at beregne det, især hvis du har med en lille matrix at gøre. Men hvis du har brug for mere komplekse beregninger eller et grundigt dobbelttjek af din beslutning, er det bedre at bruge denne online lommeregner. Med dens hjælp kan du hurtigt og præcist løse en omvendt matrix.

Ved at bruge denne online lommeregner kan du gøre dine beregninger meget nemmere. Derudover er det med til at konsolidere det materiale, der opnås i teorien - det er en slags simulator for hjernen. Det bør ikke betragtes som en erstatning for manuelle beregninger, det kan give dig meget mere, hvilket gør det lettere at forstå selve algoritmen. Desuden skader det aldrig at dobbelttjekke sig selv.

Definition 1: en matrix kaldes ental, hvis dens determinant er nul.

Definition 2: en matrix kaldes ikke-singular, hvis dens determinant ikke er lig med nul.

Matrix "A" kaldes omvendt matrix, hvis betingelsen A*A-1 = A-1 *A = E (enhedsmatrix) er opfyldt.

En kvadratisk matrix er kun inverterbar, hvis den er ikke-singular.

Skema til beregning af den inverse matrix:

1) Beregn determinanten af ​​matrix "A" if ∆ A = 0, så eksisterer den inverse matrix ikke.

2) Find alle algebraiske komplementer af matrix "A".

3) Opret en matrix af algebraiske tilføjelser (Aij)

4) Transponer matrixen af ​​algebraiske komplementer (Aij )T

5) Multiplicer den transponerede matrix med den inverse af determinanten for denne matrix.

6) Udfør kontrol:

Ved første øjekast kan det virke kompliceret, men faktisk er alt meget enkelt. Alle løsninger er baseret på simple aritmetiske operationer, når man løser, er det ikke at blive forvekslet med "-" og "+"-tegnene og ikke miste dem.

Lad os nu løse en praktisk opgave sammen ved at beregne den inverse matrix.

Opgave: find den inverse matrix "A" vist på billedet nedenfor:

Vi løser alt nøjagtigt som angivet i planen for beregning af den inverse matrix.

1. Den første ting at gøre er at finde determinanten for matrix "A":

Forklaring:

Vi har forenklet vores determinant ved hjælp af dens grundlæggende funktioner. Først tilføjede vi til 2. og 3. linje elementerne i den første linje, ganget med et tal.

For det andet ændrede vi 2. og 3. kolonne af determinanten, og i henhold til dens egenskaber ændrede vi tegnet foran den.

For det tredje tog vi den fælles faktor (-1) ud af den anden linje og ændrede derved tegnet igen, og det blev positivt. Vi har også forenklet linje 3 på samme måde som i begyndelsen af ​​eksemplet.

Vi har en trekantet determinant, hvis elementer under diagonalen er lig med nul, og ved egenskab 7 er den lig med produktet af de diagonale elementer. Til sidst fik vi ∆ A = 26, derfor eksisterer den inverse matrix.

A11 = 1*(3+1) = 4

A12 = -1*(9+2) = -11

A13 = 1*1 = 1

A21 = -1*(-6) = 6

A22 = 1*(3-0) = 3

A23 = -1*(1+4) = -5

A31 = 1*2 = 2

A32 = -1*(-1) = -1

A33 = 1+(1+6) = 7

3. Det næste trin er at kompilere en matrix ud fra de resulterende tilføjelser:

5. Multiplicer denne matrix med det inverse af determinanten, det vil sige med 1/26:

6. Nu mangler vi bare at tjekke:

Under testen modtog vi en identitetsmatrix, derfor blev løsningen udført helt korrekt.

2 måde at beregne den inverse matrix på.

1. Elementær matrixtransformation

2. Invers matrix gennem en elementær konverter.

Elementær matrixtransformation inkluderer:

1. Multiplicer en streng med et tal, der ikke er lig med nul.

2. Tilføjelse af en linje til en linje ganget med et tal.

3. Skift rækkerne i matrixen.

4. Ved at anvende en kæde af elementære transformationer får vi en anden matrix.

EN -1 = ?

1. (A|E) ~ (E|A -1 )

2.A -1 * A = E

Lad os se på dette ved hjælp af et praktisk eksempel med reelle tal.

Øvelse: Find den inverse matrix.

Løsning:

Lad os tjekke:

En lille forklaring på løsningen:

Først omarrangerede vi række 1 og 2 i matrixen og gangede derefter den første række med (-1).

Derefter gangede vi den første række med (-2) og tilføjede den med den anden række i matrixen. Så gange vi linje 2 med 1/4.

Den sidste fase af transformationen var at gange den anden linje med 2 og tilføje den med den første. Som et resultat har vi en identitetsmatrix til venstre, derfor er den inverse matrix matrixen til højre.

Efter kontrol var vi overbevist om, at beslutningen var korrekt.

Som du kan se, er beregningen af ​​den inverse matrix meget enkel.

I slutningen af ​​dette foredrag vil jeg også gerne bruge lidt tid på egenskaberne ved sådan en matrix.

I den første del så vi på, hvordan man finder den inverse matrix ved hjælp af algebraiske tilføjelser. Her vil vi beskrive en anden metode til at finde inverse matricer: ved hjælp af Gauss- og Gauss-Jordan-transformationerne. Denne metode til at finde den inverse matrix kaldes ofte metoden til elementære transformationer.

Elementær transformationsmetode

For at anvende denne metode skrives den givne matrix $A$ og identitetsmatrixen $E$ ind i én matrix, dvs. danner en matrix af formen $(A|E)$ (denne matrix kaldes også udvidet). Herefter sikres det ved hjælp af elementære transformationer udført med rækkerne i den udvidede matrix, at matricen til venstre for linjen bliver identitet, og den udvidede matrix har formen $\left(E| A^(- 1) \right)$. Elementære transformationer i denne situation omfatter følgende handlinger:

1. Udskiftning af to linjer.
2. Multiplicer alle elementer i en streng med et tal, der ikke er lig med nul.
3. Tilføjelse til elementerne i en række af de tilsvarende elementer i en anden række ganget med en hvilken som helst faktor.

Disse elementære transformationer kan anvendes på forskellige måder. Normalt vælges Gauss-metoden eller Gauss-Jordan-metoden. Generelt er Gauss og Gauss-Jordan metoderne beregnet til at løse systemer af lineære algebraiske ligninger, og ikke til at finde inverse matricer. Udtrykket "at bruge den Gaussiske metode til at finde den inverse matrix" skal her forstås som "at bruge de operationer, der er iboende i den Gaussiske metode til at finde den inverse matrix."

Nummereringen af ​​eksempler fortsætter fra første del. Eksemplerne diskuterer brugen af ​​Gauss-metoden til at finde den inverse matrix, og eksemplerne diskuterer brugen af ​​Gauss-Jordan-metoden. Det skal bemærkes, at hvis alle elementer i en bestemt række eller kolonne i matrixen, der er placeret før linjen, nulstilles til nul, så eksisterer den inverse matrix ikke.

Eksempel nr. 5

Find matrixen $A^(-1)$ hvis $A=\left(\begin(array) (ccc) 7 & 4 & 6 \\ 2 & 5 & -4 \\ 1 & -1 & 3 \end( array) \right)$.

I dette eksempel vil den inverse matrix blive fundet ved hjælp af Gauss-metoden. Den udvidede matrix, som generelt har formen $(A|E)$, vil i dette eksempel have følgende form: $ \left(\begin(array) (ccc|ccc) 7 & 4 & 6 & 1 & 0 & 0 \\ 2 & 5 & -4 & 0 & 1 & 0 \\ 1 & -1 & 3 & 0 & 0 & 1 \end(array) \right)$.

Mål: Brug elementære transformationer til at bringe den udvidede matrix til formen $\left(E|A^(-1) \right)$. Lad os anvende de samme operationer, som bruges, når vi løser systemer af lineære ligninger ved hjælp af Gauss-metoden. For at anvende Gauss-metoden er det praktisk, når det første element i den første række af den udvidede matrix er en. For at opnå dette bytter vi den første og tredje række i den udvidede matrix, som bliver: $ \left(\begin(array) (ccc|ccc) 1 & -1 & 3 & 0 & 0 & 1 \\ 2 & 5 & - 4 & 0 & 1 & 0 \\ 7 & 4 & 6 & 1 & 0 & 0 \end(array) \right)$.

Lad os nu komme til løsningen. Gauss-metoden er opdelt i to faser: frem og tilbage (en detaljeret beskrivelse af denne metode til løsning af ligningssystemer er givet i eksemplerne på det tilsvarende emne). De samme to trin vil blive anvendt i processen med at finde den inverse matrix.

Lige slag

Første skridt

Ved hjælp af den første linje nulstiller vi elementerne i den første kolonne, der er placeret under den første linje:

Lad mig kommentere lidt på den udførte handling. Notationen $II-2\cdot I$ betyder, at de tilsvarende elementer i den første række, tidligere ganget med to, blev trukket fra elementerne i den anden række. Denne handling kan skrives separat som følger:

Handling $III-7\cdot I$ udføres på nøjagtig samme måde. Hvis der er vanskeligheder med at udføre disse operationer, kan de udføres separat (svarende til handlingen $II-2\cdot I$ vist ovenfor), og resultatet kan derefter indtastes i den udvidede matrix.

Andet trin

Ved hjælp af den anden linje nulstiller vi elementet i den anden kolonne, der er placeret under den anden linje:

Divider den tredje linje med 5:

Den direkte flytning er slut. Alle elementer placeret under matrixens hoveddiagonal op til linjen nulstilles.

Omvendt slag

Første skridt

Ved hjælp af den tredje linje nulstiller vi elementerne i den tredje kolonne, der er placeret over den tredje linje:

Inden vi går videre til næste trin, lad os dividere den anden linje med $7$:

Andet trin

Ved hjælp af den anden linje nulstiller vi elementerne i den anden kolonne, der er placeret over den anden linje:

Transformationerne er afsluttet, den inverse matrix findes ved hjælp af Gauss-metoden: $A^(-1)=\left(\begin(array) (ccc) -11/5 & 18/5 & 46/5 \\ 2 & -3 & -8 \ \7/5 & -11/5 & -27/5 \end(array) \right)$. Kontrollen kan om nødvendigt udføres på samme måde som i de foregående eksempler. Hvis du springer alle forklaringerne over, vil løsningen se sådan ud:

Svar: $A^(-1)=\left(\begin(array) (ccc) -11/5 & 18/5 & 46/5 \\ 2 & -3 & -8 \\ 7/5 & -11/ 5 & ​​​​-27/5 \end(array) \right)$.

Eksempel nr. 6

Find matrixen $A^(-1)$ hvis $A=\left(\begin(array) (cccc) -5 & 4 & 1 & 0 \\ 2 & 3 & -2 & 1 \\ 0 & 7 & -4 & -3 \\ 1 & 4 & 0 & 6 \end(array) \right)$.

For at finde den inverse matrix i dette eksempel, vil vi bruge de samme operationer, som bruges, når vi løser systemer af lineære ligninger ved hjælp af Gauss-metoden. Detaljerede forklaringer er givet i, men her vil vi begrænse os til korte kommentarer. Lad os skrive den udvidede matrix: $\left(\begin(array) (cccc|cccc) -5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \\ 2 & 3 & -2 & 1 &0 &1&0 &0 \ \ 0 & 7 & -4 & -3 &0 & 0 & 1 & 0\\ 1 & 4 & 0 & 6 & 0 &0 & 0 & 1 \end(array) \right)$. Lad os bytte første og fjerde række i denne matrix: $\left(\begin(array) (cccc|cccc) 1 & 4 & 0 & 6 &0 &0 & 0 & 1 \\ 2 & 3 & -2 & 1 &0 &1&0 &0 \ \0 & 7 & -4 & -3 &0 & 0 & 1 & 0\\ -5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \end(array) \right)$.

Lige slag

Fremadgående konverteringer er fuldført. Alle elementer placeret under matrixens hoveddiagonal til venstre for linjen nulstilles.

Omvendt slag

Den inverse matrix blev fundet ved hjælp af Gauss-metoden, $A^(-1)=\left(\begin(array) (cccc) -13/14 & -75/8 & 31/8 & 7/2 \\ -19 /8 & - 117/16 & 49/16 & 11/4 \\ -23/4 & -141/8 & 57/8 & 13/2 \\ 17/8 & 103/6 & -43/16 & - 9/4 \ end(array)\right)$. Om nødvendigt udfører vi kontrollen på samme måde som i eksempel nr. 2 og nr. 3.

Svar: $A^(-1)=\left(\begin(array) (cccc) -13/14 & -75/8 & 31/8 & 7/2 \\ -19/8 & -117/16 & 49 /16 & 11/4 \\ -23/4 & -141/8 & 57/8 & 13/2 \\ 17/8 & 103/6 & -43/16 & -9/4 \end(array) \ højre) $.

Eksempel nr. 7

Find matrixen $A^(-1)$ hvis $A=\left(\begin(array) (ccc) 2 & 3 & 4 \\ 7 & 1 & 9 \\ -4 & 5 & -2 \end( array) \right)$.

For at finde den inverse matrix anvender vi operationer, der er karakteristiske for Gauss-Jordan-metoden. Forskellen fra Gauss-metoden, diskuteret i tidligere eksempler og, er, at løsningen udføres i et trin. Lad mig minde dig om, at Gauss-metoden er opdelt i 2 trin: fremadgående bevægelse ("vi laver" nuller under matrixens hoveddiagonal til linjen) og det omvendte træk (vi nulstiller elementerne over matrixens hoveddiagonal til linjen). For at beregne den inverse matrix ved hjælp af Gauss-Jordan-metoden kræves der ikke to løsningstrin. Lad os først oprette en udvidet matrix: $(A|E)$:

$$ (A|E)=\left(\begin(array) (ccc|ccc) 2 & 3 & 4 & 1 & 0 & 0\\ 7 & 1 & 9 & 0 & 1 & 0\\ -4 & 5 & ​​​​-2 & 0 & 0 & 1 \end(array) \right) $$

Første skridt

Lad os nulstille alle elementer i den første kolonne undtagen én. I den første kolonne er alle elementer ikke-nul, så vi kan vælge et hvilket som helst element. Lad os tage $(-4)$ for eksempel:

Det valgte element $(-4)$ er i den tredje linje, så vi bruger den tredje linje til at nulstille de valgte elementer i den første kolonne:

Lad os gøre det første element i den tredje række lig med én. For at gøre dette skal du dividere elementerne i den tredje række i den udvidede matrix med $(-4)$:

Lad os nu fortsætte med at nulstille de tilsvarende elementer i den første kolonne:

I yderligere trin vil det ikke længere være muligt at bruge den tredje linje, fordi vi allerede har brugt den i første trin.

Andet trin

Lad os vælge et bestemt ikke-nul-element i den anden kolonne og nulstille alle andre elementer i den anden kolonne. Vi kan vælge et af to elementer: $\frac(11)(2)$ eller $\frac(39)(4)$. Elementet $\left(-\frac(5)(4) \right)$ kan ikke vælges, fordi det er placeret i den tredje linje, som vi brugte i forrige trin. Lad os vælge elementet $\frac(11)(2)$, som er i den første linje. Lad os sikre os, at der i stedet for $\frac(11)(2)$ i den første linje er en:

Lad os nu nulstille de tilsvarende elementer i den anden kolonne:

Den første linje kan ikke bruges i yderligere diskussioner.

Tredje trin

Vi skal nulstille alle elementer i den tredje kolonne undtagen én. Vi skal vælge et element, der ikke er nul, i den tredje kolonne. Vi kan dog ikke tage $\frac(6)(11)$ eller $\frac(13)(11)$, fordi disse elementer er placeret i den første og tredje linje, som vi brugte tidligere. Valget er lille: kun elementet $\frac(2)(11)$ er tilbage, som er i anden linje. Lad os dividere alle elementer i den anden linje med $\frac(2)(11)$:

Lad os nu nulstille de tilsvarende elementer i den tredje kolonne:

Transformationer ved hjælp af Gauss-Jordan-metoden er afsluttet. Tilbage er blot at sikre, at matrixen bliver enhed op til linjen. For at gøre dette skal du ændre rækkefølgen af ​​linjerne. Lad os først bytte første og tredje linje:

$$ \left(\begin(array) (ccc|ccc) 1 & 0 & 0 & 47/4 & -13/2 & -23/4 \\ 0 & 0 & 1 & -39/4 & 11/2 & 19/4 \\ 0 & 1 & 0 & 11/2 & -3 & -5/2 \end(array) \right) $$

Lad os nu bytte den anden og tredje linje:

$$ \left(\begin(array) (ccc|ccc) 1 & 0 & 0 & 47/4 & -13/2 & -23/4 \\ 0 & 1 & 0 & 11/2 & -3 & - 5/2 \\ 0 & 0 & 1 & -39/4 & 11/2 & 19/4 \end(array) \right) $$

Så $A^(-1)=\left(\begin(array) (ccc) 47/4 & -13/2 & -23/4 \\ 11/2 & -3 & -5/2 \\ - 39/4 & 11/2 & 19/4 \end(array) \right)$. Naturligvis kan løsningen udføres på en anden måde ved at vælge elementer placeret på hoveddiagonalen. Det er normalt, hvad de gør, for i dette tilfælde, i slutningen af ​​løsningen, er der ingen grund til at bytte linjer. Jeg gav den forrige løsning kun til ét formål: at vise, at valget af linje ved hvert trin ikke er vigtigt. Hvis du vælger diagonale elementer ved hvert trin, vil løsningen se sådan ud.

At finde den inverse matrix- et problem, der ofte løses på to måder:

• metoden med algebraiske tilføjelser, som kræver at finde determinanter og transponere matricer;
• den Gaussiske metode til at eliminere ukendte, som kræver at udføre elementære transformationer af matricer (tilføj rækker, gange rækker med det samme tal osv.).

For dem, der er særligt nysgerrige, er der andre metoder, for eksempel metoden med lineære transformationer. I denne lektion vil vi analysere de tre nævnte metoder og algoritmer til at finde den inverse matrix ved hjælp af disse metoder.

Invers matrix EN, kaldes en sådan matrix

EN
. (1)

Invers matrix , som skal findes for en given kvadratisk matrix EN, kaldes en sådan matrix

produktet, hvoraf matricerne EN til højre er identitetsmatrixen, dvs.
. (1)

En identitetsmatrix er en diagonal matrix, hvor alle diagonale elementer er lig med én.

Sætning.For hver ikke-singular (ikke-degenereret, ikke-singular) kvadratisk matrix kan man finde en invers matrix, og kun én. For en speciel (degenereret, singulær) kvadratisk matrix eksisterer den inverse matrix ikke.

Den kvadratiske matrix kaldes ikke speciel(eller ikke-degenereret, ikke-ental), hvis dens determinant ikke er nul, og særlig(eller degenerere, ental) hvis dens determinant er nul.

Det omvendte af en matrix kan kun findes for en kvadratisk matrix. Naturligvis vil den inverse matrix også være kvadratisk og af samme orden som den givne matrix. En matrix, for hvilken der kan findes en invers matrix, kaldes en inverterbar matrix.

For omvendt matrix Der er en relevant analogi med det omvendte af et tal. For hvert nummer -en, ikke lig med nul, er der et sådant tal b at arbejdet -en Og b er lig med en: ab= 1. Antal b kaldes det omvendte af et tal b. For eksempel for tallet 7 er den reciproke 1/7, da 7*1/7=1.

At finde den inverse matrix ved hjælp af metoden med algebraiske additioner (allieret matrix)

Til en ikke-singular firkantet matrix EN det omvendte er matrixen

hvor er matricens determinant EN, a er en matrix forbundet med matrixen EN.

Allieret med en kvadratisk matrix EN er en matrix af samme orden, hvis elementer er de algebraiske komplementer af de tilsvarende elementer af determinanten af ​​matricen transponeret i forhold til matrix A. Således, hvis

At

Og

Algoritme til at finde den inverse matrix ved hjælp af metoden med algebraiske additioner

1. Find determinanten for denne matrix EN. Hvis determinanten er lig med nul, stopper det at finde den inverse matrix, da matrixen er ental, og dens inverse eksisterer ikke.

2. Find matrixen transponeret mhp EN.

3. Beregn elementerne i unionsmatrixen som algebraiske komplementer til maritz fundet i trin 2.

4. Anvend formel (2): gange det inverse af matrixdeterminanten EN, til unionsmatrixen fundet i trin 4.

5. Tjek resultatet opnået i trin 4 ved at gange denne matrix EN til den omvendte matrix. Hvis produktet af disse matricer er lig med identitetsmatrixen, så blev den inverse matrix fundet korrekt. Ellers skal du starte løsningsprocessen igen.

Eksempel 1. Til matrix

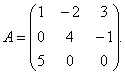
find den inverse matrix.

Løsning. For at finde den omvendte matrix skal du finde determinanten for matricen EN. Vi finder efter reglen om trekanter:

Derfor matrixen EN– ikke-ental (ikke-degenereret, ikke-ental) og der er en omvendt for det.

Lad os finde en matrix forbundet med denne matrix EN.

Lad os finde matricen transponeret i forhold til matricen EN:

Vi beregner elementerne i den allierede matrix som algebraiske komplementer til matrixen transponeret i forhold til matrixen EN:

Derfor er matrixen allieret med matrixen EN, har formen

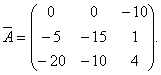
Kommentar. Rækkefølgen for beregning af elementer og transponering af matricen kan være anderledes. Du kan først beregne de algebraiske komplementer af matricen EN, og transponer derefter den algebraiske komplementmatrix. Resultatet skal være de samme elementer i unionsmatrixen.

Ved at anvende formel (2) finder vi matrixen invers i forhold til matrixen EN:

At finde den inverse matrix ved hjælp af Gaussisk ukendt eliminationsmetode

Det første trin til at finde det inverse af en matrix ved hjælp af Gauss-elimineringsmetoden er at tildele til matrixen EN identitetsmatrix af samme rækkefølge, der adskiller dem med en lodret streg. Vi får en dobbelt matrix. Lad os gange begge sider af denne matrix med , så får vi

,

Algoritme til at finde den inverse matrix ved hjælp af Gaussisk ukendt eliminationsmetode

1. Til matrixen EN tildele en identitetsmatrix af samme rækkefølge.

2. Transformer den resulterende dobbeltmatrix, så du på venstre side får en enhedsmatrix, så får du på højre side, i stedet for identitetsmatrixen, automatisk en invers matrix. Matrix EN på venstre side omdannes til identitetsmatrixen ved elementære matrixtransformationer.

2. Hvis i færd med matrix transformation EN ind i identitetsmatrixen vil der kun være nuller i enhver række eller i en hvilken som helst kolonne, så er determinanten af ​​matricen lig med nul, og følgelig matrixen EN vil være ental, og den har ikke en invers matrix. I dette tilfælde stopper yderligere bestemmelse af den inverse matrix.

Eksempel 2. Til matrix

find den inverse matrix.

og vi vil transformere det, så vi på venstre side får en identitetsmatrix. Vi begynder forvandlingen.

Multiplicer den første række i venstre og højre matrix med (-3) og læg den til den anden række, og gange derefter den første række med (-4) og læg den til den tredje række, så får vi

.

For at sikre, at der ikke er brøktal i efterfølgende transformationer, lad os først oprette en enhed i den anden række på venstre side af den dobbelte matrix. For at gøre dette skal du gange den anden linje med 2 og trække den tredje linje fra den, så får vi

.

Lad os tilføje den første linje med den anden, og derefter gange den anden linje med (-9) og tilføje den med den tredje linje. Så får vi

.

Divider så den tredje linje med 8

.

Gang den tredje linje med 2 og læg den til den anden linje. Det viser sig:

.

Lad os bytte anden og tredje linje, så får vi endelig:

.

Vi ser, at vi på venstre side har identitetsmatrixen, derfor har vi på højre side den inverse matrix. Således:

.

Du kan kontrollere rigtigheden af ​​beregningerne ved at gange den oprindelige matrix med den fundne inverse matrix:

Resultatet skal være en omvendt matrix.

Eksempel 3. Til matrix

find den inverse matrix.

Løsning. Kompilering af en dobbelt matrix

og vi vil forvandle det.

Vi multiplicerer den første linje med 3 og den anden med 2, og trækker fra den anden, og derefter gange vi den første linje med 5, og den tredje med 2 og trækker fra den tredje linje, så får vi

.

Vi multiplicerer den første linje med 2 og lægger den til den anden, og trækker derefter den anden fra den tredje linje, så får vi

.

Vi ser, at i den tredje linje på venstre side er alle elementer lig med nul. Derfor er matrixen ental og har ingen invers matrix. Vi holder op med at finde den omvendte maritz.